はじめに
コンピュータは、ビット数が制限されている数値で動作できることが知られています。 原則として、32ビット整数と64ビット整数の処理に慣れています。これらは、.NETプラットフォームでは、それぞれInt32(int)型とInt64(long)型に対応しています。
また、29などの数字を想像する必要がある場合はどうすればよいでしょうか。 = 884176199373970195454361616000000? このような数値は、64ビットのデータ型ではなく、32ビットのデータ型には収まりません。
長い算術演算が存在するような大きな数を扱うため
です。長い算術 -コンピューター技術では、ビット深度が特定のコンピューターの機械語長を超える数に対する演算(加算、乗算、減算、除算、累乗など)。 これらの操作はハードウェアではなく、ソフトウェアで実装され、基本的なハードウェアを使用して多数の低次数で動作します。
ロング算術は、オリンピックプログラミングのセクションの1つと考えることもできます。これは、問題を解決する際に、標準タイプでは最終結果を表すのに十分でないことが非常に多いためです。 olympiadのニーズに合ったプログラミング言語を選択する場合、組み込みのツールセット(既製のライブラリ、実装されたクラス)は重要ではありません。 多くの言語(Java、Ruby、Python)には長い算術演算が組み込まれているため、プログラムの作成にかかる時間を大幅に短縮できます。
バージョン4.0までの.NETプラットフォームには、長い数字を扱うための組み込みのサポートがありませんでした。 4番目のバージョンでは、.NETは長いだけでなく、複素数も取得しました。 この機能は
System.Numericsアセンブリを介して利用でき、
BigIntegerおよび
Complex型は、アセンブリと同じ名前の名前空間で定義されます。
BigInteger構造は
.NET 3.5に
表示されるはずでしたが、その時点では完全に準備が整っていなかったため、その実装はすべてのニーズを満たしていなかった(パフォーマンスの問題も原因と考えられる)ため、終了を.NETに延期することにしました4.0。
この記事では、Microsoftのlong算術の実装の詳細を検討します。
一般的な概念
コンピュータのメモリで長い数字を表すという考え方は非常に簡単です。 10進数システムの123456789を検討してください。 明らかに、次のように表すことができます。
123456789
10 = 1 * 10
8 + 2 * 10
7 + 3 * 10
6 + 4 * 10
5 + 5 * 10
4 + 6 * 10
3 + 7 * 10
2 + 8 * 10
1 + 9 * 10
0一般に、任意の数は次のように表すことができます。
A = a n- 1βn -1 + a n- 2βn -2 + ... + a 1β+ a 0ここで、βは数を表す数体系の基数であり、係数a
iは二重不等式0≤a
i <βを満たします。
数値の表現は、多項式の表現を連想させます。適切な程度のxの代わりに、必要な程度の底βがあります。 既知のように、多項式a
0 + a
1 x + a
2 x
2 + ... + a
n x
nは、要素が係数a
iを表す配列の形式で表すのが便利で、インデックスiは対応する次数xを決定します。 長い数値も同様に保存され、ベースβの選択を決定します。
たとえば、同じ番号123456789は、次のように1万(β= 10
4 )の数値システムで表すことができます。
123456789
10 = 1 *(10
4 )
2 + 2345 *(10
4 )
1 + 6789 *(10
4 )
010,000桁の数値システムで123456789という数値を表すと、2つの利点が同時に得られます。1つは、9つの数値の配列ではなく3つの数値の配列(1、2345および6789)一度に4桁の数字を処理するため、長い数字の標準操作の実行時間を短縮します。 一般に、コンピューターは1ビットと32ビットの数値を同じようにすばやく加算するため、これを使用する必要があります。
通常、数値システムβのベースは、コンピューター上のベースデータ型の最大サイズに依存し、次の考慮事項に基づいて選択されます。
- ベースは、基本データ型のいずれかに適合しなければなりません。
- 基数は、長い数の表現のサイズを小さくして操作の速度を上げるためにできるだけ大きくする必要がありますが、係数を持つすべての操作が基本データ型を使用するように十分に小さくする必要があります
- 出力とデバッグの利便性のために、10の累乗としてβを選択できます。β-2の累乗を使用すると、低レベルで高速操作を実行できます。
また、数値の符号は別の変数で考慮されることに注意してください。つまり、配列には長い数値のモジュールが含まれ、数値も逆方向に格納されます。 これは主に便宜上行われました。数値の符号を格納できる配列のゼロ/最後の要素を特別に処理する必要はなく、すべての操作は最下位から最上位まで実行されます。
MicrosoftのBigInteger
Reflectorまたは
dotPeekデコンパイラーを介して
BigInteger構造を見ると、次のフィールドが表示されます。
private static readonly BigInteger s_bnMinInt = new BigInteger(-1, new uint[1]{ (uint) int.MinValue }); private static readonly BigInteger s_bnOneInt = new BigInteger(1); private static readonly BigInteger s_bnZeroInt = new BigInteger(0); private static readonly BigInteger s_bnMinusOneInt = new BigInteger(-1); internal int _sign; internal uint[] _bits; private const int knMaskHighBit = -2147483648; private const uint kuMaskHighBit = 2147483648U; private const int kcbitUint = 32; private const int kcbitUlong = 64; private const int DecimalScaleFactorMask = 16711680; private const int DecimalSignMask = -2147483648;
構造体には2つのインスタンスフィールド(_signおよび_bits)のみが含まれ、残りのフィールドは定数、および数値-1、0、1の構造体値を表す静的読み取りフィールドです。
数値の符号は変数_signに格納され、_bits配列には係数a
iが含まれると仮定できます。 _bits配列のタイプがuint []である場合、βの底が2 2
32のべき乗であると仮定することもできます(uintは32ビット符号なし数値であるため)。
したがって、我々は仮定を確認または反論しようとします。
intをとるコンストラクターは、引数として次のようになります。
intを受け入れるコンストラクター public BigInteger(int value) { if (value == int.MinValue) { this = BigInteger.s_bnMinInt; } else { this._sign = value; this._bits = (uint[]) null; } }
その実装により、_sign変数の目的についてもう少し知ることができます。 ご覧のとおり、長い数値がintの範囲(-2 31〜2
31 -1)に配置されると、_sign変数に格納され、_bits配列は使用されず、nullになります。 この最適化により、
BigInteger型の作業が高速化されるだけでなく、実際に数値が大きくない場合に消費されるメモリのサイズが削減されます。
どうぞ
uintを引数として取るコンストラクタは次のようになります。
コンストラクターホストuint public BigInteger(uint value) { if (value <= (uint) int.MaxValue) { this._sign = (int) value; this._bits = (uint[]) null; } else { this._sign = 1; this._bits = new uint[1]; this._bits[0] = value; } }
数値がint範囲に配置されるかどうかに応じて、_sign変数または_bits配列のいずれかに書き込まれます。
次のコンストラクタは、64ビットの符号付き数値(長い)を受け入れ、数値システムの基数の選択に関する質問に答えるのに役立ちます。
コンストラクターホストロング public BigInteger(long value) { if ((long) int.MinValue <= value && value <= (long) int.MaxValue) { if (value == (long) int.MinValue) { this = BigInteger.s_bnMinInt; } else { this._sign = (int) value; this._bits = (uint[]) null; } } else { ulong num; if (value < 0L) { num = (ulong) -value; this._sign = -1; } else { num = (ulong) value; this._sign = 1; } this._bits = new uint[2]; this._bits[0] = (uint) num; this._bits[1] = (uint) (num >> 32); } }
数値がintの範囲に収まらない場合、ご覧のとおり、_sign変数には数値の符号(負の場合は-1、正の場合は1)が含まれ、_bits配列には同じ係数a
iが含まれ、次のように入力されます。
this._bits = new uint[2]; this._bits[0] = (uint) num; this._bits[1] = (uint) (num >> 32);
この場合、64ビットの数値numは、(uint)numと(uint)(num >> 32)の2つの32ビット数値に分割されます。 最初の数値はnumの最後の32ビットで、2番目の数値は最初の32ビットです(nビットだけ右にシフトすることは、整数を2
nで除算することと同等です)。
数値long.MaxValue = 2
63 -1 = 9223372036854775807が
BigInteger構造に格納される方法を決定しましょう。 これを行うには、2
32で除算します。
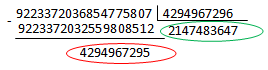
実際には(uint)long.MaxValue = 4294967295、(uint)(long.MaxValue >> 32)= 2147483647。
したがって、9223372036854775807 = 2147483647 *(2
32 )
1 + 4294967295 *(2
32 )
0 、および
BigInteger
ペアで表されます:
_sign = 1
_bits = {4294967295、2147483647} //数値は逆方向に保存されることを覚えておいてください長い番号-1234567891011121314151617181920の場合:

つまり、数は次のように2
32の累乗で拡張されます。
1234567891011121314151617181920 = 15 *(2
32 )
3 + 2501550035 *(2
32 )
2 + 3243814879 *(2
32 )
1 + 4035623136 *(2
32 )
0したがって、
BigIntegerはペアで表されます。
_sign = -1 //数値の符号
_bits = {4035623136、3243814879、2501550035、15}たとえば17のint範囲に収まる数値は、次のように格納されます。
_sign = 17
_bits = nullBigInteger構造体のコンストラクター
を調べ
たら 、次のように結論付けることができます。
- 数値がint範囲にある場合、変数_signに格納されます。
- 数値がint範囲に収まらない場合、その符号は変数_sign(負の場合は-1、正の場合は1)に格納され、_bits配列には2 32を底とする長整数の展開の係数a iが含まれます。
低レベルで2のべき乗(2のべき乗の乗算と除算はビットの左右シフトに対応)で作業する方が簡単であり、一度に32桁の数値が処理されるため、ベースβ= 2
32が適切な選択です。それらに対して操作を実行します。
一般に、
BigInteger構造は、.NETプラットフォームでの長い演算の本格的な実装です。 同時に、Microsoftはプリミティブな数値型にできるだけ近づけようとしました
。BigIntegerインスタンスは、他の整数型と同じように使用できます。
BigIntegerは標準の数値演算子をオーバーロードして、加算、減算、除算、乗算、減算、否定、単項否定などの基本的な数学演算を実行します。 標準の数値演算子を使用して、2つのBigInteger値を互いに比較することもできます。 他のタイプの整数と同様に、
BigIntegerはビット演算子And、Or、XOR、左シフト、右シフトをサポートしています。
ユーザー定義演算子をサポートしない言語の場合、
BigInteger構造体は、数学演算を実行するための同等のメソッドも提供します。 これは、加算、除算、乗算、否定、減算などのメソッドに適用されます。 Microsoftは、
Decimalフレームワークの実装でもまったく同じことを行いました。
BigInteger構造体の多くのメンバーは、他の整数型のメンバーに直接対応しています。 さらに、
BigIntegerは次のような要素を追加します。
- IsEven-数値が偶数かどうかを判断します。
- IsPowerOfTwo-数値が2のべき乗かどうかを判断します。
- 符号-BigInteger数の符号を示す値を返します。
- Abs-BigInteger数の絶対値を返します。
- DivRem-商と除算の剰余を返します。
- GreatestCommonDivisor-2つの数値の最大公約数を返します。
- Log-指定された基数を持つ数値システムの指定された数値の対数を返します。
- 最大/最小-2つの数値の最大/最小を返します。
- ModPow-数値を別の数値の累乗でモジュラー除算します。
- Pow-BigIntegerの値を指定された程度まで上げます。
MonoおよびJavaでのBigIntegerに関するいくつかの言葉
Monoは、長い演算もサポートしていることに注意してください。 Monoでの
BigInteger構造の実装は、intで表される数値の最適化がないことを除いて、Microsoftの実装と実質的に変わりません。
つまり、Monoの番号17はペアで表されます。
_sign = 1 //数値の符号
_bits = {17}BigIntegerの同様の実装がJavaで提供されています。
public class BigInteger extends Number implements Comparable<BigInteger> { int signum; int[] mag; private int bitCount = -1; private int bitLength = -1; private int lowestSetBit = -2; private int firstNonzeroByteNum = -2; private int firstNonzeroIntNum = -2; private final static long LONG_MASK = 0xffffffffL; }
Javaには符号なしの型がないため、mag配列はint []型です。 したがって、Javaと.NETでの長い数値の表現は異なります。 .NETでは、uint型の範囲が広いため、プレゼンテーションの効率が少し向上します。
コンストラクターホストロング private BigInteger(long val) { if (val < 0) { signum = -1; val = -val; } else { signum = 1; } int highWord = (int)(val >>> 32); if (highWord == 0) { mag = new int[1]; mag[0] = (int)val; } else { mag = new int[2]; mag[0] = highWord; mag[1] = (int)val; } }
JavaとMonoでは、intで表される数値の最適化はありません。
BigIntegerのパフォーマンス
長い
BigInteger番号を使用する場合、潜在的なパフォーマンスの問題に注意する必要があります。 たとえば、一見無害な演算子++は、パフォーマンスに大きな影響を与える可能性があります。
int length = 1000000; BigInteger num = BigInteger.Parse("12345678910111213141516171819"); for (int i = 2; i < length; i++) { if (IsPrime(i)) num++; } Console.WriteLine(num);
この例では、既存のオブジェクトの値が変わるようですが、そうではありません。
BigIntegerオブジェクトは不変です。つまり、内部では、共通言語ランタイムが実際に新しい
BigIntegerオブジェクトを作成し、以前のオブジェクトよりも1つ大きい値を割り当てます。
この例では、次のことができます。通常の数値型を使用して中間操作を実行し、
BigIntegerを使用します。
int length = 1000000; BigInteger num = BigInteger.Parse("12345678910111213141516171819"); int temp = 0; for (int i = 2; i < length; i++) { if (IsPrime(i)) temp++; } num += temp; Console.WriteLine(num);
他の.NET Framework数値型も不変です。 ただし、
BigInteger型には上限または下限がないため、その値は非常に大きな値に成長し、パフォーマンスに測定可能な影響を与える可能性があります。
結論の代わりに
要約すると、バージョン4以降の.NETプラットフォームは、
整数の長演算の本格的な実装を獲得したと言えます。 おそらく、完全な幸福のために、長い間.NET BCLのベータステータスに存在していた
BigRational構造を実装することが残っています。
BigRational構造の説明:
BigRational構造
は 、.NET Framework 4で導入された
BigInteger型に基づいており、任意の精度の有理数を作成できます。 有理数は2つの整数の比率であり、
BigRational構造のこの実装では、
BigInteger型が被除数(分子)および除数(分母)として使用されます。
コメントをありがとう:
gouranga