こんにちは、私はHabrahabrを長い間読んでおり、しばしばニューラルネットワークに関する記事、特に単層パーセプトロンに関する記事に出会いました。 しかし、これまでのところ、パーセプトロンタイプの他のタイプの認識機能に関する記事はありませんでした。 記事の名前が示すように、このタイプの認識機能は
潜在機能の方法と呼ばれてい
ます 。
この記事の目的は、この方法に基づいて動作するプログラムを提供することではなく、アルゴリズム自体、それが何に基づいており、どのような利点があるのかを伝えることです。
まず、この記事で使用されているパターン認識の理論の基本概念を説明し、次にその方法を簡単に説明してから、詳細に説明します。
基本的な概念画像-受容器官へのオブジェクトのマッピング。 つまり、一連の記号としてのオブジェクトの説明。 多くの場合、オブジェクトはベクトルとして表されます。 符号のセットが一定の場合、オブジェクトはその画像で識別されます。
画像(クラス)は、多くのオブジェクトまたは画像のサブセットです。
決定的な機能は、オブジェクトが特定のクラスに属するかどうかを決定する画像が決定される入力での機能です。
簡単な説明パターン認識に使用されるアルゴリズムのこのメソッドの本質は、オブジェクトごとに目的のクラスに属することを決定する決定的な関数を構成することです。
この場合、決定的な関数は、マークされたトレーニングサンプル(OBの各オブジェクトのクラスが既知である)に従って繰り返しコンパイルされます。
物理的な解釈n次元のメトリック空間を想像してください。nはオブジェクトを記述するために必要な特徴の数です。
クラスW1に属するトレーニングサンプル(以下OBと呼びます)のすべてのオブジェクトが、オブジェクトに対応するポイントで最大値をとり、距離とともに急速に減少する正のポテンシャルを作成し、クラスW2に属するオブジェクトが負であるとします。
次に、クラスW1のオブジェクトが優勢な領域では、プラスの可能性があり、その逆も同様です。
実際、トレーニングセットの各オブジェクトには、分類されたオブジェクトを対応するクラスに「引き付ける」料金が割り当てられます。
潜在的な機能メソッド自体に移りましょう。 まず、実際の潜在的な機能について説明します。 物理的解釈のセクションから明らかなように、ここでは電荷と可能性との類似性を引き出します。 したがって、必要な関数として、特定のポイントで最大値を与え、距離が長くなるとすぐに減少する関数を取得する必要があります。
潜在的な関数をK(x、xk)として示します。xk、k = 1..mは、トレーニングセットのオブジェクト(ベクトル)の1つです。
通常、対称関数は潜在的な関数、2つの変数-XとXkとして使用されます。
たとえば、K(x、xk)= exp {-a || x-xk || ^ 2}
決定的な機能。 累積ポテンシャル。決定的な関数として、累積ポテンシャル-オブジェクトがクラスw1に属する場合は個々のポテンシャル関数の値の正のセット、オブジェクトがクラスw2に属する場合は負の値を使用します。
累積ポテンシャルは次のとおりです。
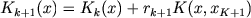
ここで、Rk + 1 =
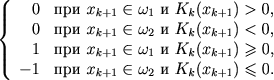
アルゴリズムの終了条件は、連続したL0オブジェクトのエラーのない決定です。 ここで、L0はユーザーが指定した番号です。 次の事実に基づいて、必要なアルゴリズムの品質に応じて設定されます。
pは、サンプルオブジェクトのLkを提示した後にエラーを起こす確率です。
次に、e> 0およびa> 0の場合、p <eが1-aより大きい確率は
L0>ログ(ea)/ログ(1-e)
おわりに 長所と短所。最終的に、特定の関数K(x)を取得します。この関数は、このオブジェクトが特定のエラー確率で2つのクラスのいずれかに属するかどうかを決定します。
潜在的な関数の方法の利点は、多くのオブジェクトの非線形パーティションです。 これにより、他の方法では解決が難しい問題を解決できます。
欠点は、適切な潜在的な関数の選択が難しいことと、大量のトレーニングサンプルを使用した計算の複雑さです。
記事はやや簡潔であることが判明しましたが、あなた自身のために何か新しいことを学んだことを願っています。 主なアイデアは、舞台裏で、決定関数と収束率を見つけるためのアルゴリズムの収束の数学的正当化と、潜在的な関数のより厳密な数学的定義であると言いました。
この記事の目的は、パターン認識に使用される他のあまり一般的でない方法について話すことでした。 興味があれば、この問題に対する確率的および論理的アプローチについても知ることができます。