
nビットの助けを借りて誰もが知っているように、最大2
n -1までカウントするカウンターを実装できますが、リソースが非常に限られている場合、またはシーケンス、確率、ランダム性、カウンター増加を1つに実験して組み合わせたい場合は、 。
この記事では、いわゆる確率的カウンターの仕組みを説明します。
1977年に、彼のフレーズで知られるBellLabsで働く暗号作成者であるRobert Morrisによって最初に導入されました。
「コンピューターのセキュリティに関する3つのゴールデンルール:コンピューターを所有したり、電源を入れたり、使用したりしないでください。」
メーターの詳細
tビットを自由に使用できます。
負ではない増加シーケンスn
i (iは0〜2
t -1の範囲にあります)を選択し、少し先に進んで、n
iの値がカウンタ値になると言います。
最も興味深いのは、1にカウンターを追加する確率が1 /(n
i + 1 -n
i )になることです。
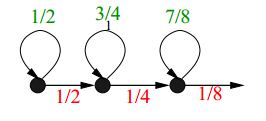
たとえば、シーケンスがn
i = i
2の場合、カウンターを8から増やすと1 /(16-8)= 0.125の確率で真になり、その結果、n
iからn
i + 1へのカウンターはn
i + 1だけで平均して増えます-n
i操作
確率的カウンターの特殊なケースはn
i = iであり、このようなシーケンスではカウンターが正常になり、追加の確率が1になることは明らかです。
実装
それでは、実際に実行してみましょう。
Java言語で実装します。
一定のメモリが8GBしかないとします。 重要なので、スコアを127に保つことができますが、これでは十分ではありません。
問題は、どのシーケンスを使用するかです。 彼女の選択は、メーターを保持する期間と、精度を犠牲にする意思があるかどうかによって異なります。 任意の整数の昇順シーケンスを自由に使用できます。たとえば、
オンラインシーケンスエンサイクロペディアで検索できます。
フィボナッチ数と
数の 二乗を使用し
ます 。
2つの主な機能があります。 最初はカウンタをインクリメントし、2番目はシーケンスのi番目の番号を返します。
private byte counter = 0; public void increase(){ Random rand = new Random(); int randNumber = rand.nextInt(getElementSequence(counter + 1) - getElementSequence(counter)); if(randNumber == 0) counter++; }
ここでは、確率に応じてカウンタが増加します。 カウンターはシーケンスについて何も知らず、イベントの成功または失敗に応じて、i番目の要素のみを返します。
これが二乗数列です
private int getElementSequence(int number){ return (int) Math.pow(number, 2); }
しかし、フィボナッチ数から
private int getElementSequence(int number){ int sumFib = 1; int previousElement = 0; int temp; for(int i = 0; i < number + 1; i++){ temp = sumFib; sumFib = sumFib + previousElement; previousElement = temp; } return sumFib; }
10,000回の反復で、通常のサイクルでカウンターの増加をシミュレートします。
public static void main(String[] args) { TestApproximateCounting test = new TestApproximateCounting(); for(int i=0; i<10000; i++){ test.increase(); }; }
まとめると
シーケンスごとに、10,000回の繰り返しのカウンターを10回実行しました
| 実行番号 | 二乗数のカウンター値 | 数の二乗 | フィボナッチ数のカウンター値 | フィボナッチ数 |
|---|
| 1 | 93 | 8 649 | 20 | 6 765 |
| 2 | 111 | 12 321 | 20 | 6 765 |
| 3 | 105 | 11 025 | 20 | 6 765 |
| 4 | 103 | 10 609 | 21 | 10 946 |
| 5 | 96 | 9,216 | 21 | 10 946 |
| 6 | 94 | 8 836 | 22 | 17 711 |
| 7 | 93 | 8 639 | 19 | 4 181 |
| 8 | 106 | 11,236 | 19 | 4 181 |
| 9 | 104 | 10 816 | 21 | 10 946 |
| 10 | 94 | 8 836 | 20 | 6 765 |
ご覧のとおり、エラーは非常に顕著ですが、8ビットで10,000を超えるカウントが必要な場合は、確率的カウンターが適切なオプションです。
参照:
Kormen T.、Leiserson C.、Rivest R.、Stein K.-アルゴリズム。 構築と分析-2005
Morris、R.小さなレジスターで多数のイベントをカウントします。 ACM 21、10(1977)、840〜842の通信
UPD。 リクエストに応じて、各シーケンスのカウンター値を示す2つの列をテーブルに追加しましたが、ここでも、カウンター自体の値は、カウンターからではなく、入力に対するカウンターを持つgetElementSequence関数から取得されると言います。