Geekly Articles each Day

減価償却分析

こんにちは、Habr！

今日は減価償却分析についてお話します。 まず、それが何であるかを説明し、おもちゃの例を挙げます。 そして、それを使用して互いに素なシステムを分析する方法を説明します。


減価償却分析


減価償却分析は、複数回実行されるアルゴリズムに使用されます。 アルゴリズムの時間は大きく変動する可能性がありますが、すべての開始の平均時間または合計時間を推定します。 ほとんどの場合、アルゴリズムはデータ構造に対して何らかの操作を実装します。

「減価償却」という言葉自体は金融から来ました。 それは、ローンを返済するための小さな定期的な支払いを意味します。 一般的なケースでは、高速オペレーションは低速オペレーションのコストを時間とともに補うことを意味します。

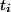
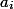
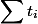
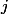
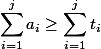
操作のシーケンスを検討する 。 すべての操作 実際に時間内に実行されます 。 この時間は実際と呼ばれます。 各操作について 減価償却時間を計算します 。 今回は、評価を容易にするために紹介します 。 これにより、次の2つの制限があります。 不等式が成り立つ 、およびb）非公式-減価償却費の額は簡単に考慮されるべきです。

目の前に具体的な例を示すために、スタックが存在するデータ構造を検討します。 データ構造はop(m, x)操作をサポートします。これは最後の 要素を挿入し、要素を挿入します 。

 def op(stack, m, x): for i in range(m): stack.pop() stack.push(x)

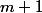
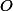
引数は常に正しいと仮定し、スタック上にあるものよりも多くをスローする必要はありません。 さらに、 op(m, x)は、 なしでステップ -表記法。 すべての推定値に定数を常に掛けて、正しい推定値を得ることができます。

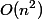
時間操作op(m, x)は1から ステップ。 大まかな見積もりは時間を与えます すべてを満たすために 操作。

減価償却分析には、3つの評価方法があります。

銀行の方法。 時は金なり


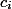
すべての時間単位をコインにします。 各手術を配る コインと過ごすことができます 。 すべてのオペレーションコインは、データ構造に従って配置できます。 1つの操作の減価償却費は 。

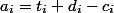
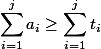
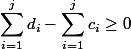
不変式をサポートするには 、制限を設定します：現在より多くのコインを使うことはできません： 。 以来 それから 。

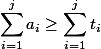
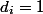
この例では、各操作に1コイン（ ） スタックに追加したばかりのアイテムの上に置きます。 したがって、我々はこのアイテムの将来のPOPに対して支払いました。

スタックの各要素には、コイン、つまり すべてのPOPはプリペイドです。

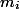
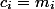
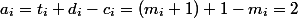
捨てる 私たちはそれらの上にあるすべてのコインを費やす要素（ ） 次に、各トランザクションの減価償却費 。 それに気づくために残ります 。 最高の線形性能推定値を得ました 操作。

物理学メソッド。 あなたの可能性を活用


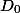
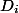
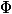
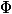
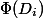
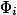
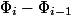
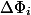
どのデータ構造も、いくつかの状態を取ります。 させて すべての操作の前の初期状態であり、 -後の状態 番目の操作。 潜在的な機能を紹介します 、入力としてデータ構造の現在の状態を取り、負でない数を返します。 可能性 初期状態はゼロでなければなりません。 簡単にするために、 を通して 、そして を通して 。 減価償却費 。

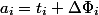
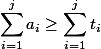
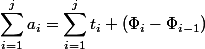
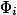
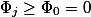
不変量 ポテンシャルの定義に従います。 確かに ; すべて 最初と最後を除いて、削減され、 。 以来 それから 。

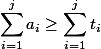
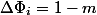
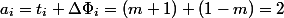
一般的な考え方は、実際の時間を補い、費用のかかる操作では劇的に低下し、安価な操作では少し大きくなる可能性のある関数を見つけることです。 この例では、スタック上の要素の数が適切です。 後 POPとワンPUSH 。 次に減価償却費 、再び線形推定値を取得します。

集約方法。 あなたはすべてを取り、共有する必要があります


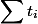
この方法は、前の2つの方法の一般化であり、何らかの方法で計算することです。 クエリの数で割ります。

私たちの場合、この推論は機能します。 各op(m, x)操作は、1つのPUSHと複数のPOPを実行します。 スタックから配置するよりも多くの要素をスタックからスローすることはできません。 スタックに置く 要素、これ以上投げない 。 合計時間は 。 1つの操作の減価償却費 。

ばらばらの集合システム


彼らは私たちに与えた 要素。 要素を組み合わせてセットにすることができます。 3つの操作をサポートするデータ構造を作成したい



これらの操作をサポートするデータ構造は、disjoint set system（SNM）（disjoint-setデータ構造、union-findデータ構造、またはmerge-findセット）と呼ばれます。

ハブですでにSNMについて書いています。 ここでアルゴリズムとそのアプリケーションの詳細な説明を見つけることができます 。 この投稿では、アルゴリズム自体を簡単に思い出し、分析に焦点を当てます。

アルゴリズム


ツリーの形で保存する各セット。 ツリーノードには、親への参照が格納されます。 ノードがルートの場合、リンクはNone指します。 さらに、各ノードには追加のrankフィールドがあります。 以下で説明します。

 class Node: def __init__(self, key): self.parent = None self.rank = 0 self.key = key

セットを処理するには、各セットの代表者を選択します。 この場合、それはツリーのルートになります。 2つの要素の代表が同じ場合、それらは同じセットにあります。 2つのセットを結合するには、一方のツリーをもう一方のルートにサスペンドする必要があります。 簡単なアルゴリズムを取得します。

 def find(x): if x.parent == None: return x return find(x.parent) def union(x, y): x = find(x) y = find(y) y.parent = x return x

アルゴリズムを高速化するために、2つのヒューリスティックが使用されます。

グレード 。 各ノードには、最初はゼロに等しいランクが割り当てられます。 ツリーのランクは、そのルートのランクです。 セットを結合するとき、より低いランクのツリーをより大きなツリーにぶら下げます。 ランクが一致する場合、最初にツリーの1つのランクを1つ増やします。

 def union(x, y): x = find(x) y = find(y) if x.rank < y.rank: x, y = y, x if x.rank == y.rank: x.rank += 1 y.parent = x return x

SNMの作業を高速化するには、ランクヒューリスティックだけで十分です。 最悪の場合の操作。 しかし、さらに先に進みます。

パス圧縮 要素からfindを実行しましょう 。 途中のすべてのピークが ルートにすぐにルートに中断することができます。



 def find(x): if x.parent == None: return x x.parent = find(x.parent) return x.parent

驚くべきことに、これらの2つのヒューリスティックにより、1つの操作の減価償却時間がほぼ一定に短縮されます。

分析


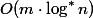
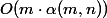
1973年、HopcroftとUllmanは、2つのヒューリスティックプロセスを持つSNM の操作 どこで -反復対数。 その後、1975年、タージャンはSNMが どこで アッカーマンの逆関数です。

私の計画は、まずこれらのトリッキーな関数を整理し、次に最悪の場合の単純な対数推定を証明し、最終的にホップクロフトとウルマンの推定を分解することです。 Tarjanの評価では、減価償却分析も幅広く使用していますが、技術的な詳細が含まれています。

トリッキーな機能


反復対数は、電力塔の逆数です。 のような数字を想像してみましょう 2つだけがある場所 。 それから そのような最小値は そのパワータワーの高さ もっとなります 。 正式に



読者を練習して、宇宙の既知の部分の粒子数の反復対数が5を超えないことを示します。

パワータワーは急速に成長していると思われるかもしれませんが、20世紀初頭の数学者にとってこれは十分ではなく、アッカーマン関数を考え出しました。 次のように定義されます。



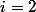
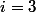
この機能は非常に急速に成長しています。 で それは力の塔です。 で また、それは発電塔でもありますが、今ではタワー内の2の数も発電塔などです。

敵に復venしたい場合は、算術演算、ifs、forsのみを使用してこの関数を計算するように依頼します（while-sおよび再帰は許可されません）。 アッカーマンは彼が失敗することを証明した。

アッカーマン逆関数 最小として定義 そのような 。 成長が非常に遅いことは容易に理解できます。

最悪の場合のスコア


まず、各unionは2つのfind操作と追加の時定数で実行されることに注意してください。 したがって、 findのみを評価するだけで十分です。 最悪の場合の推定値は、2つの単純な観測から得られます。

観察1 。 ランクツリー 少なくとも含む ノード。

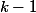
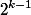
このステートメントは帰納法によって証明されます。 ランク0のツリーの場合、明らかに。 ランクツリーを取得するには 2つのランクツリーを結合する必要がある 、それぞれで少なくとも ノード。 だからランクツリーで 少なくとも ノード。

その結果、任意の時点で、ランクのノード もうなくなります 、および最大ノードランク 。

備考2 。 親のランクは、常に子のランクよりも大きくなります。

それは建設から続きます。 ランクは常にトップからルートへの途中で増加するため、その長さは超えません 、およびfindは 。

ホップクロフトとウルマンのスコア


それを証明しましょう SNM操作オーバー 要素を保持することができます 。

make_set操作make_set実行されます 。 union操作-のため さらに、2つのfind操作の時間。 したがって、次のことを示すだけで十分です。 find操作はで実行されます 。

find操作の実行時間は、指定されたノードからルートまでのパスの長さに比例します。 したがって、ノードごとのパスの総数を評価する必要があります。

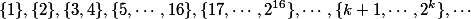
すべてのランクを分割する セット： 。 で -thセットは、パワータワーからのすべてのランクになります 高さ タワーの高さまで 。 ノードのランクが存在するセットの番号は、ノードのレベルと呼ばれます。

ツリーのルート、ルートの直接の子、またはノードとその親が異なるレベルにある場合、ノードは適切であると言います。 残りのノードは不良と呼ばれます。

合計レベルはもうありません 。 したがって、任意のノードからルートへのパスには、 良い結び目。 合計で、 findはこれ以上パスしません 良い結び目。

不良ノードでのパスの数を推定します。 悪い結び目をしましょう ランクがあります 、そして 多くに属する 。 不良ノードはルートではないため、ランクが固定されていることに注意してください。 findがノードを通過する場合 それから 親を上位の新しい親に変更します。 せいぜい 通過する 悪い結び目のような 良くなります。

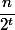
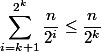
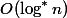
合計ランクノード もうない 。 したがって、セットのランクを持つノード もうなくなります 。 各ノードについて、これ以上 悪い結び目にあるかのように、通路。 パスの合計でこれ以上はありません 。 合計レベル 。 したがって、不良ノードを通過するパスはもうありません。 。

合計で最高評価を獲得 合計ですべての操作に対して。

文学


Source: https://habr.com/ru/post/J208624/

More articles:


All Articles