天体力学に関する記事はHabréで人気を博しているので、伝えることにしました
1つの基本的な運動方程式、つまりケプラーの方程式について。
ご存知のように、太陽系の天体の有限運動は楕円で発生します。 ただし、必要に応じて
天体が特定の時点にあるポイントを確立するには、この情報では不十分であり、ケプラー方程式を使用する必要があります。
この方程式を導き出します。
楕円は平坦化された値であることを思い出させてください
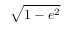
円。 ここで、eは離心率です。
楕円の面積は等しい

ここで、aは半長軸です。
ケプラーの2番目の法則によれば、天体の半径ベクトルによって掃引される領域は時間に比例するということで、次のように記述できます。

ここで、Tは軌道周期、tは現在時刻、t0は近日点(太陽に最も近い軌道点)の通過時刻です。
ここで、この領域の軌道上の天体の位置、つまり半径ベクトルrの大きさと真の異常、つまり太陽から見た近日点と天体の間の角度への依存関係を見つけましょう。
これを行うために、追加の変数-異常な異常Eを導入します。
楕円の焦点の1つに位置する太陽(原点)からx軸を、後線(近心点と近心点を結ぶ線)に沿って近日点に向けてみましょう。
また、楕円の半長軸に等しい半径を持つ補助円を作成します。

点Pでの天体の横座標は、

縦座標はそれぞれ
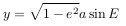
したがって、
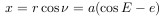
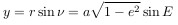
面積Sを計算するために、補助図を考慮します。
円のセクターP'-O-Per:
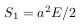
PO-Per楕円セクター:
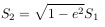
トライアングルO-O'-P:

セクターP-O'-Per:
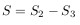
ここから、面積Sは次と等しくなります。
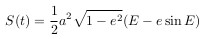
この式を以前に導出されたケプラーの第2法則と比較すると、
私達は得る:
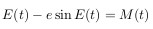
ここで、M(t)= 2 * pi *(t-t0)/ T
これはケプラー方程式です。
これはEの超越方程式であり、一般的な場合、明示的な解を得ることができないことに注意してください。
天体の座標を計算するには、既知のMとeから偏心異常を見つけてから、上記の式に従って半径ベクトルと角度、必要に応じてxとyを決定する必要があります。
興味深い質問は、ケプラー方程式を解く方法を見つけることです。
人類の最高の精神は、過去400年間、これを行ってきました。
その結果、多くの興味深いアイデアで数学が充実しましたが、これを説明するには別の記事が必要です。