はじめに
こんにちは、読者の皆様。
Pythonで時系列の分析に関する
以前の投稿を書いた後、コメントに示されたコメントを修正することにしましたが、それらを修正するとき、たとえば、季節のARIMAモデルを構築するときなど、いくつかの問題に遭遇しました
statsmodelsパッケージに同様の関数が見つかりませんでした。 結局、私はこのために
Rの関数を使用することに決め、検索により
rpy2ライブラリに移動しました。これにより、前述の言語のライブラリの関数を使用できます。
多くの人が「なぜこれが必要なのか」と尋ねるかもしれません。なぜなら、
Rを取得して、その中ですべての作業を行う方が簡単だからです。 私はこの声明に完全に同意しますが、データに予備処理が必要な場合、
Pythonでデータを生成する方が簡単で、必要に応じて正確に
R機能を分析に使用できるように思えます。
さらに、関数Rの出力結果を
IPython Notebookに統合する方法を示します
。Rpy2をインストールして構成する
開始するには、rpy2をインストールする必要があります。 次のコマンドを使用してこれを行うことができます。
pip install rpy2
このライブラリが機能するためには、インストールされた
R言語が必要であることに注意してください。
オフからダウンロードできます
。 サイト次に行うことは、必要なシステム変数を追加することです。 Windowsの場合、次の変数を追加します。
- PATH -R.dllおよびR.exeへのパス
- R_HOME -Rがインストールされているフォルダーへのパス
- R_USER -Windowsがロードされるユーザー名
インストールは、操作データが不要なMac OS Xでも実行されました。
はじめに
したがって、
IPython Notebookで作業している場合は、命令を追加する必要があります。
%load_ext rmagic
この拡張機能を使用すると、
rpy2を介して
特定の R関数を呼び出し、IPython Notebookコンソールに結果を直接表示できます。これは非常に便利です（これを行う方法を以下に示します）。 詳細は
ここに書かれてい
ます 。
次に、必要なライブラリをダウンロードします。
from pandas import read_csv, DataFrame, Series import statsmodels.api as sm import rpy2.robjects as R from rpy2.robjects.packages import importr import pandas.rpy.common as com from pandas import date_range
ここで、前の記事と同様に、データをロードして、毎週の間隔に進みます。
dataset = read_csv('DataSets/tovar_moving.csv',';', index_col=['date'], parse_dates=['date'], dayfirst=True) otg = dataset.qty w = otg.resample('w', how='sum') w.plot(figsize=(12,6))
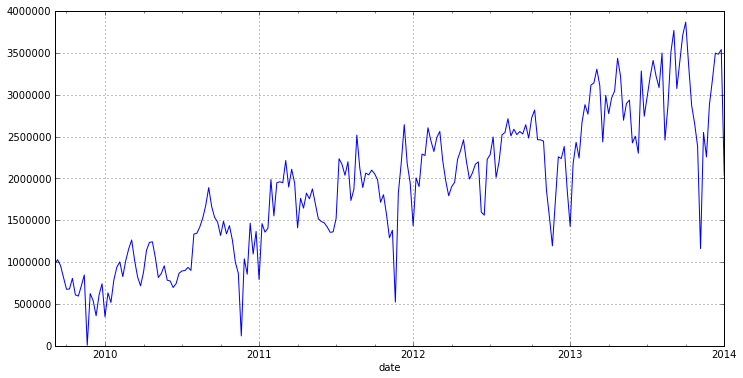
したがって、グラフから、年間の季節性（52週間）と顕著な傾向を確認できます。 したがって、モデルを構築する前に、傾向と季節性を取り除く必要があります。
予備データ分析
したがって、まず最初に、元のシリーズをプロローグして値を調整します。
w_log = log(w) w_log.plot(figsize=(12,6))
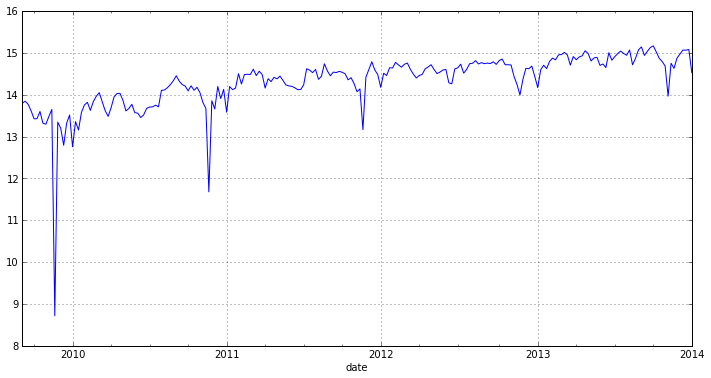
ご覧のとおり、グラフには季節性があるため、系列は定常的ではありません。
Dickey-Fullerテストを使用し
てこれを検証します。この
テストでは、単位根の存在の仮説をチェックします。したがって、存在する場合、系列は静止しません。 前回、
statsmodelsライブラリを使用してこのテストを実行する方法を示しました。 次に、
Rの adf.test（）関数を使用してこれを行う方法を示します
。したがって、この関数は
tseries Rライブラリにあります。 時系列分析用に設計されており、オプションです。
importr（）関数を使用して、目的のライブラリをロードできます。
stats = importr('stats') tseries = importr('tseries')
tseriesに加えて、
統計ライブラリもダウンロードしたことに気付くかもしれません。 型変換に必要です。
次に、データをPythonタイプから理解可能なRのタイプに変換する必要があります。これは、
convert_to_r_dataframe（）関数を使用して、DataFrameが入力される入力に変換できます。出力は
Rのベクトルです。 r_df = com.convert_to_r_dataframe(DataFrame(w_log))
したがって、ベクトルは次のステップであり、時系列の形式に変換する必要があります。 このため、Rには関数
ts（）があり、その呼び出しは次のようになります。
y = stats.ts(r_df)
予備データの準備が完了し、必要な関数を呼び出すことができます。
ad = tseries.adf_test(y, alternative="stationary", k=52)
パラメータとして、テストが計算される時系列とラグの数が渡されます。 経済モデルでは、この値を年と等しくすることが慣習的であり、 週ごとのデータがあり、1年で52週間なので、パラメーターにはそのような値があります。
広告変数にRオブジェクトが含まれるようになりました。 その構造はリストとして記述されていますが、その記述は見つけることができませんでした。 したがって、視覚的な分析を使用して、関数の結果をわかりやすい方法で表示するコードを作成しました。
a = ad.names[:5] {ad.names[i]:ad[i][0] for i in xrange(len(a))}
{「代替」：「静止」、
'method'： '拡張ディッキーフラーテスト'、
「p.value」：0.23867869477446427、
「パラメータ」：52.0、
「統計」：-2.8030060277420006}
テスト結果に基づいて、最初の系列は定常的ではありません。 なぜなら 単位根の存在の仮説は低い確率で受け入れられ、したがって、系列は定常的ではありません。 次に、定常性について、いくつかの最初の違いを確認します。
まず、Pythonを使用してそれらを取得し、次にADFテストを適用します。
diff1lev = w.diff(periods=1).dropna() print 'p.value: %f' % sm.tsa.adfuller(diff1lev, maxlag=52)[1]
p値：0.000000
diff1lev.plot(figsize=(12,6))
テスト結果によると、多くの最初の違いは定常的であることが判明しました。 そして、グラフはトレンドがないことを確認するのに役立ちます。 季節性を取り除くために残っています。
これを行うには、結果のシリーズから季節の違いをとる必要があります。 詳細は
こちら 。 結果の行が静止している場合は、最初の違いを編んで確認する必要があります。
diff1lev_season = diff1lev.diff(52).dropna()
RのADFテストを使用して、定常性を確認しましょう。
r_df = com.convert_to_r_dataframe(DataFrame(diff1lev_season)) y = stats.ts(r_df) ad = tseries.adf_test(y, alternative="stationary", k=52) a = ad.names[:5] {ad.names[i]:ad[i][0] for i in xrange(len(a))}
{「代替」：「静止」、
'method'： '拡張ディッキーフラーテスト'、
「p.value」：0.551977997289418、
「パラメータ」：52.0、
「統計」：-2.0581183466564776}
そのため、シリーズは静止していません。最初の違いを確認してください。
diff1lev_season1lev = diff1lev_season.diff().dropna() print 'p.value: %f' % sm.tsa.adfuller(diff1lev_season1lev, maxlag=52)[1]
p.value：0.000395
結果の行は静止しています。 これで、モデルの構築に進むことができます
モデルの構築。
これで予備分析が完了し、
季節モデルARIMA （SARIMA）の構築に進むことができます。
このモデルの一般的なビュー
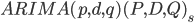
このモデルでは、パラメーターは以下を示します。
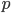-モデル次数 
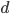-ソースデータの統合の順序
-モデル次数 
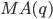
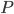-季節成分の順序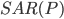 
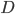-季節成分を統合する手順- -季節成分の順序
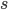-季節性の次元（月、四半期など）
p 、
d 、
qの決定方法は、前回示しました。 次に、
P 、
D 、
Qの季節成分の順序の決定について説明します
。パラメーター
Dを定義することから始めます
。 季節差の統合の順序、つまり 私たちの場合、それは
1に等しいです。
Pと
Qを決定するには
、 ACRと
PACFの相関図を作成する必要があります。
fig = plt.figure(figsize=(12,8)) ax1 = fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(diff1lev_season1lev.values.squeeze(), lags=150, ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(diff1lev_season1lev, lags=150, ax=ax2)
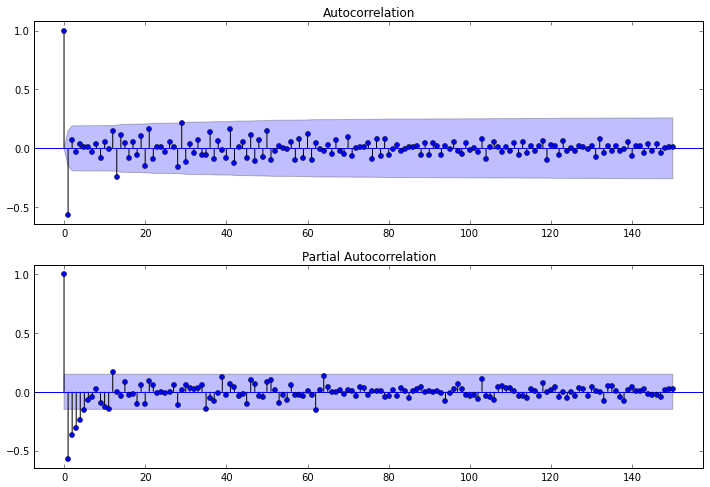
PACF
garfikから、AR次数は
p = 4であり、
ACFによれば次数MA
q = 13であることが
わかります。 13ラグは、0以外の最後のラグです。
それでは、季節の要素に移りましょう。 それらを評価するには、季節性のサイズの倍数であるラグを調べる必要があります。つまり、この例では、季節性が52である場合、ラグ52、104、156、...
この場合、パラメーター
Pと
Qは0に等しくなります（これは、上記の遅れでACFとPACFを見るとわかります）。
私たちの研究の結果、モデルを得ました
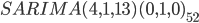
この記事の冒頭で示したように、このモデルをPythonで作成する方法を見つけられなかったため、Rの
arima（）関数を使用することにしました。このため、ARIMAモデルの順序と、必要に応じて季節成分の順序が渡されます。 しかし、呼び出す前に、いくつかのデータを準備する必要があります。
まず、ソースセットをR形式に変換し、時系列形式に変換します。
r_df = com.convert_to_r_dataframe(DataFrame(w)) y = stats.ts(r_df)
モデルの順序はベクトルRとして渡されるため、作成しましょう。
order = R.IntVector((4,1,13))
また、季節コンポーネントのパラメーターとして、その順序と期間のサイズを含むリストが渡されます。
season = R.ListVector({'order': R.IntVector((0,1,0)), 'period' : 52})
これで、モデルを作成する準備ができました。
model = stats.arima(y, order = order, seasonal=season)
これでモデルの準備が整い、それに基づいて予測の構築に進むことができます。
モデルの妥当性を確認します。
そのため、モデルの妥当性を確認するには、モデルの残りが「ホワイトノイズ」に対応しているかどうかを確認する必要があります。
肺-ボックスQテストを実行してこれを検証し、残留物の相関を検証します。 これを行うには、Rにtsdiag（）関数があり、テストのモデルとラグの数がパラメーターとして渡されます。
この関数は次のように呼び出すことができます。
%Rpush model %R tsdiag(model, 100)
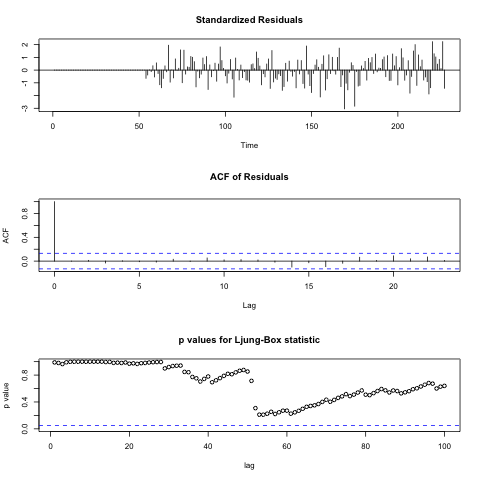
1行目の
％Rpush命令は、Rで使用するオブジェクトをロードします2行目の
％Rステートメントは、R言語形式のコードを呼び出します。
上記のグラフから、残差が独立していることがわかります（これは
ACFから見ることができます）。 さらに、Q統計のグラフから、すべての点で
p値が有意水準よりも大きいことがわかります。これから、残基が「ホワイトノイズ」である可能性が最も高いと結論付けることができます。
予測
実行するには、
予測ライブラリをロードする必要があります
forecast = importr('forecast')
予測結果を導き出すには2つの方法があります。
方法1.これは、前のセクションで示したIPythonとRの統合機能を使用することです。
%R plot(forecast(model))
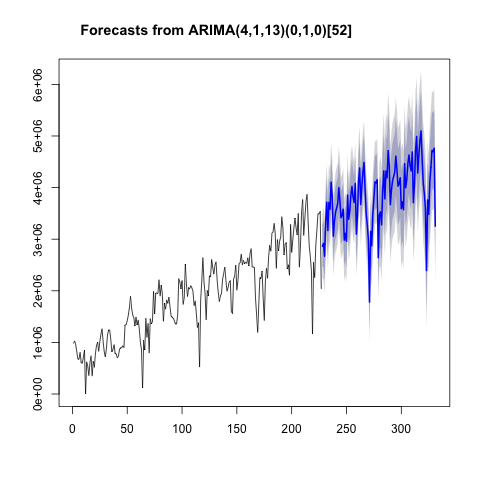方法2。2番目の方法は、予測ライブラリを使用して予測を作成し、その結果を一時的なパンダシリーズに変換して画面に表示することです。 実行されるコードは次のとおりです。
f = forecast.forecast(model)
結果を表示する
w.plot(figsize=(12,6)) pr.plot(color = 'red')
おわりに
結論として、季節性をより正確に分析するには、7〜10シーズンのデータが必要です。 さらに、記事を準備する過程で支援してくれた
werwooolfに感謝します。
この記事では、季節ごとのARIMAモデルの作成方法を示し、データ分析に多数の
Rおよび
Python言語を使用する方法も示しました。 ガールフレンドの言語の専門家は、記述された束を効果的に適用する方法を見つけると思います。