5月、Habréで、科学界で大きな反響を引き起こした素数論の分野におけるYitang Zhangの研究を説明する
記事が公開されました。 この記事では、この作品の公開から9か月後に科学界が達成した結果の概要を説明します。
数論における重要であるがまだ証明されていない仮説の1つは双子の素推測仮説であり、2つの異なる素数のペアが無限に存在することを前提としていることを思い出してください。たとえば、(3、 5); (11、13)など。この場合、もちろん、無限に多くの素数があると仮定されます-これはユークリッドによって証明された事実です。 より厳密な形式では、双子素数に関するこの仮説は次のように定式化できます。

どこで

n番目の素数を示します。 この制限の存在の証明は、元の仮説の証明につながります。 Zhangは、無限数の素数に対して区間の有限推定がある
という証拠を提供した最初の人物です。 上記の表記を使用すると、Zhangの結果は次のように記述できます。
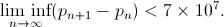
脱線して次のように言うことが重要です。
1.これは、すべての素数の間隔が70,000,000未満であるという意味ではなく、実際、nが大きいほど、2つの素数間の平均距離が大きくなり、小さい素数のペアを見つける可能性が低くなります。互いからの距離。 このトピックに関するウィキペディアの関連
記事を参照してください。
2.これは、自然数を取得しても、区間プラスマイナス70 000 000で素数を見つけることが保証されることを意味しません。
3.証明は、あなたがどれだけ遠くに行っても自然数がどれほど大きくても、これらの素数の間隔が70,000,000未満になるように、常に軸に沿って配置された一対の素数があることです。
この研究は大きな共鳴を引き起こし、多くの科学者にこの境界をさらに改善するよう促しました。 私たちの時代で最も才能のある数学者の一人である
テレンスタオは 、同僚のグループとともに、実証済みの上限を減らすことを目標とした集団プロジェクト
polymath8aを組織しました。 わずか数か月で、私たちの共同の努力により、チャンの結果が大幅に改善され、
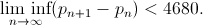
現在、
ドラフト (注意、177ページ)を読むことができますが、この作業の結果は出版のために準備されています。
2013年11月19日、次のブレークスルーが続きました。 ジェームズ・メイナード
は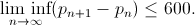
独創的なテレンス・タオは途方に
暮れず、新しい国境の改善を目的とした新しい集団プロジェクト
polymath8bを組織しました。 最終結果
は 、
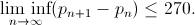
したがって、無限数の素数のペアがあり、その間隔が270を超えないことが知られています。潜在的に、別の仮説を証明できる場合、この境界は6に減らすことができます(数学では、一方の仮説の証明が他方の証明/たとえば、フェルマーの定理でした)。
ただし、この場合でも、数学者を実質的に近づけることはできますが、これは最終的な目標である双子の素数仮説の証明にすぐにはつながりません。