
100階建ての建物と2つのガラス玉のタスクは、インターネットコミュニティに長い間
悩まされてきました(
Habrahabr 、
LJ 、
フォーラム )。 好奇心mind盛な心は確かに自分自身に問いかけます。一般的な場合、床が
n 個、ボールが
k個あるとき何をすべきか?
n = 2
40 、
k = 10の場合に(少なくともおよそ)何回のスローが必要になるとしましょうか?
ネットワークの広大さと私自身の研究で見つかった情報を組み合わせることで、この問題を解決するための重要なアイデア、および研究中に得られた主な結果と興味深い観察についての投稿を提示したいと思います。
そのため、
条件を述べます
。k個の同一のガラス玉があります。 「
n 」階の「
x 」階以上の階から落ちた場合、「
x -1」階から下の階まで落ちた場合、それらは壊れません。
xの値
は不明であり、1から
nまでの任意の自然数にすることができます。 必須です:
1.
xを見つけることが保証されている最小試行回数(ボールスロー)を決定します(最悪の場合、その値に関係なく)。
2.上記のテスト数以下で
xを見つけることが保証されているアルゴリズムを開発します。
最小テスト数の概算
2つの極端なケースを区別するのは簡単です:
A)
ボールは1つしかあり
ません 。 次に、各フロアから、最初のフロアから順番に、分割されるか「
n -1」フロアに到達するまで、順番にスローする必要があります。 ボールが「
a 」フロア(1≤a≤n-1)でクラッシュした場合、
x =
aです。 「
n -1」番目に分割されなかった場合、
x =
n 。 最悪の場合、
n -1のテストが必要になります。
B)
多くのボールがある (つまり、k≥log
2 n )。 その後、あなたは適用することができます
検索方法「セグメントを半分に分割する」家の中央からボールを投げます(番号( n /2⌉の床から。where n /2⌉はn / 2以上の最小整数です)。 クラッシュしない場合は、建物の上半分の中央から投げます。クラッシュする場合は、建物の下半分の中央から2番目のボールを投げます。以降、同様に、建物の対応するセクションを半分に「分割」します。
最悪の場合、⌈log2 n⌉のトライアルと同じ数のボールが必要になります(突然投げるたびに壊れます)。
したがって、
テストの
最小数は ⌈log2 n⌉〜n-1
の範囲にあります 。 この数値を関数
f (
n 、
k )で示します。
たとえば、平屋と
k個のボールの場合、⌈log2100⌉= 7、100-1 = 99、7≤f(100、
k )≤99です。一般的に、
f (
n 、
k )の値は、
k 。 したがって、
f (100、1)= 99、
f (100、2)= 14
f (100、3)= 9、
f (100、4)= 8、
f (100、5)=
f (100、6)=
f (100、7)= ... = 7。
驚くべき事実:1階建ての建物の場合、
わずか5つのボールで7回の試行で
xを見つけることができます! つまり、「セグメントを半分に分割する」ことによる検索方法は万能薬ではありません-それは高速ですが、必要なボール数に関して常に最適とは限りません。
テストの最小数を計算するための繰り返し式
それでは、どのようにして
f (
n 、
k )の正確な値を見つけるのでしょうか?
最も単純な状況では、すべてが明確です:
f (
n 、1)=
n -1(ケースAを参照)、
f (
n 、
k )=⌈log2 n⌉for k≥log
2 n (ケースBを参照)数値
f (1、
k )= 0(フロアが1つしかない場合は、問題の状態に応じて望ましいフロアにもなります)。
n≥2およびk≥2の場合を考えてみましょう。最初のテストで「
a 」フロアからボールを投げ
た場合、
aは
1〜n -1の範囲であるとします(「
n 」フロアからボールを投げても意味が
ありません)。 次の2つの結果が考えられます。
出エジプト記1:ボールがクラッシュしました。 つまり、1≤x≤aです。 未探索の床、
k -1個のボール、つまり
xの検出を保証するには
、もう1つの
f (
a 、
k -1)テストが必要です。
出エジプト記2:ボールはクラッシュしませんでした。 これは、
a + 1≤x≤nを意味します。
n個 の未探索の床、
k個のボール、つまり
xを見つけることが保証されるためには
、もう1つの
f (
n -
a 、
k )テストが必要です。
その結果、「
a 」階からボールを投げた後、
xが見つかることを保証するために別のmax {
f (
a 、
k -1)、
f (
n -
a 、
k )}テストが必要になる場合があります。
テストの数を最小限にしたいので、max {
f (
a 、
k -1)、
f (
n -
a 、
k )}が最小、つまりmin
a {max {
f (
a 、
k -1) 、
f (
n -
a 、
k )}}。
したがって、
テストの
最小数は次のとおり
です 。
f (
n 、
k )= 1 + min
a {max {
f (
a 、
k -1)、
f (
n -
a 、
k )}}(式1)。
この式は、任意の
nおよび
kの f (
n 、
k )、およびボールを投げたい階数
a (
n 、
k )=
aを計算するのに十分です-値がmax {
f (
a 、
k -1)、
f (
n -
a 、
k )}は最小値に達します。
計算は、たとえば
Excelで簡単に実装でき
ます 。
誰が気にする2列目から始まる列Aに、
nの値を1から必要な値の順に書き込みます。 列Bの対応する行に、
f (
n 、1)の値、列Cに
f (
n 、2)の値などを書き込みます。右に1列シフトすると、ボールの数が1つ増えます。
n = 1の場合、関数
f (
n 、
k )の値はゼロであるため、対応する行をゼロで埋めます。
セルB3に、
f =(
n 、1)=
n -1であるため、式=
A 3-1を記述します。目的の行数までコピー(またはストレッチ)します。
セルC3に次の式を記述します。
= 1 + MIN(IF(B $ 2:B2> BIGGEST(C $ 2:C2; $ A $ 2:$ A2); B $ 2:B2; BIGGEST(C $ 2:C2; $ A $ 2:$ A2))))
CTRL + SHIFT + ENTERを
押します 配列数式を入力します。 コピー(またはストレッチ)して、必要な行数だけ下に、列を右に移動します。
a (
n 、
k )の値は、同じ原理に従って
f (
n 、
k )の計算に使用される列の右側の列で計算されます:行は
nの値に対応し、1列右へのシフトはボールの数が1つ増えることを意味します。
スクリーンショットのような状況では、
a (
n 、1)= 1であるため、3行目から始まる列Hに単位が入力されます(ケースAを参照して、常に1階からのみボールを投げます)。
セルI3に次の式を記述します。
= MAX((B $ 2:B2 <C3)*(BIGGEST(C $ 2:C2; $ A $ 2:$ A2)<C3)* $ A $ 2:$ A2)
CTRL + SHIFT + ENTERを
押します 配列数式を入力します。 コピー(またはストレッチ)して、必要な行数だけ下に、列を右に移動します。
X検索アルゴリズム
a (
n 、
k )の値がわかっている場合、
f (
n 、
k )以下のテストで検索アルゴリズム
xを記述するのは簡単です。
入り口:
nは家の床の数、
kはボールの数です。
出力:
x-目的のフロアの番号。
アルゴリズムの始まり。
ステップ1.変数を初期化します
。x := 1.ステップ2に進みます。
ステップ2.停止条件:
n = 1の場合、
xおよびSTOPを出力し、そうでない場合はステップ3に進みます。
ステップ3.番号
x -1 +
a (
n 、
k )の床からボールを投げます。 ボールがクラッシュした場合、変数の値を更新します:
n :=
a (
n 、
k )、
k :=
k -1。
ボールがクラッシュしない場合は、変数の値を更新します:
x :=
x +
a (
n 、
k )、
n :=
n -
a (
n 、
k )。 ステップ2に進みます。
アルゴリズムの終わり。
100フロアと5つのボールがある場合、7回の試行で
xを見つける方法の例を見てみましょう。
Excelで構築されたテーブルの
a (
n 、
k )の値を使用して、ボールを投げるフロアの番号を書き込み
ます 。
常に壊れている場合:
57- >
26- >
11- >
4- >
1 (壊れていない場合)->
2 (壊れていない場合)->
3たとえば、26階からボールを投げた後、クラッシュしなかった場合、
n = 31、
k = 4の状況にいることがわかります。その後、スローのシーケンスは次のようになります。
57- >
26- > 26 + 15 =
41- > 26 + 7 =
33- > 26 + 3 =
29- > 26 + 1 =
27 (壊れていない場合)-> 27 + 1 =
28 。
すべての可能なオプションを検討するつもりはありません。 「セグメントを半分に分割する」という点で、アルゴリズムが検索方法と異なることがわかります。
テストの最小数を計算するための「明示的な」式
フォーミュラ1の主な欠点は、計算に非常に多くのリソースがかかることです。 関数値のテーブルのパターンを検索して実証することにより、
k = 2および
k = 3についてのみ、この繰り返し式を自分で明示的に解決できました。 特に、最初の場合、結果は次のようになります。
f (
n 、2)=⌈

⌉。
他の考慮事項からも同様の結果が得られました:
記事 (著者
-Stebanoid )。 真実は彼女の答えです
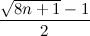
、これは問題のわずかに異なる条件によって引き起こされます-最上階から投げるときにボールが壊れる必要はありません。 この可能性を考慮したい場合、答えでは、
nの代わりに式
n + 1を置き換える(つまり、下限を追加する)必要があり、記事から式を取得します。
しかし、一般式が見つからなかったため、再帰関係が複雑すぎるため、徐々に停止しました。
irishoak 、
Bert 、
mikhail_vsなどのユーザーから、
f (
n 、
k )の計算を減らして興味深い不平等を解決できる素晴らしいアイデアを発見したのは、この瞬間でした。
これを行うには、別の関数を検討する必要があります:
g (
m 、
k )はフロアの最大数であり、その中で
k個のボールが存在する
m回のテストで
xを確実に見つけることができます。
最も単純な状況では、この関数は次の値を取ります:
g (
m 、1)=
m + 1(ケースAを参照)、
g (
m 、
k )=
g (
m 、
m )for
k >
m (
m試行は分解できるため
)最大
m個のボール、残りの
k -
m個のボールは不要であり、関数の値には影響しません)。
m≥2、
k≥2の場合、繰り返しの式を導出できます。
g (
m 、
k )=
g (
m -1、
k -1)+
g (
m -1、
k )(式2)
次の理由から簡単に理解できます。「 a 」の床からボールを投げて壊れた場合、 m -1回の試行とk -1のボールを使用して、 1〜aの範囲でxを見つけます。 このためには、 aは次の条件を満たす必要があります:a≤g( m -1、
k -1)。 したがって、ボールを投げることができる最上階はa = g ( m -1、 k -1)です。 クラッシュしない場合は、 m -1回の試行とk個のボールがあり、これを使用して別のg ( m -1、 k )フロアを探索できます。 したがって、可能な限り合計g ( m -1、 k -1)+ g ( m -1、 k )フロアを探索できます。
式1とは対照的に、式2の繰り返しは簡単に解決できます。 明示的な形式で
g (
m 、
k )を表現します。
g (
m 、
k )= C
m 0 + C
m 1 + C
m 2 + ... + C
m k 、
ここで、C
m iは
iの
mの組み合わせの数です。Cm
i =
m !/(
i !(
m -
i )!)。
この平等性は「建設的に」推定できますが、「推測」して帰納法で証明することもできますが、これははるかに簡単です(ここでは証明しません)。
ここで、テストの最小数を見つけるために、計算する必要があります:
f (
n 、
k )=⌈log2 n⌉k≥log
2 nの 場合 、
f (
n 、
k )= min {正の整数
m |
k <log
2 nの場合、 C
m 0 + C
m 1 + C
m 2 + ... + C
m k≥n}。
ところで、
g (
m 、
k )の漸化式を導出するとき、もう1つの方法は、
f (
n 、
k )のテストでボールを投げて
xを見つけることができるフロアの数を決定します:
a (
n 、
k )=
g (
m -1、
k -1)、
ここで、
m =
f (
n 、
k )、つまり
a (
n 、
k )= C
f ( n 、 k )-1 0 + C
f ( n 、 k )-1 1 + C
f ( n 、 k )-1 2 + ... + C
f ( n 、 k )- k <
f (
n 、
k )の
場合は
1 k -1 (式3)、
a (
n 、
k )= 2
f ( n 、 k ) -k≥f(
n 、
k )の
場合は
1 (式4)。
結論と最小数の試験の冒険的評価
タスクに着くと、私は直感的にソリューションプランを概説しました。最初に正しいフロアを見つける(つまりアルゴリズムを開発する)原理を理解し、次に最悪の場合に必要なスローの数を見つけます。
驚いたことに、パスは異なることが判明しました
。f (
n 、
k )で指定したテストの最小数を計算するための式から簡単なアルゴリズムを簡単にたどることができました。
関数
fについてほとんど何も知らないので、次のように概算しました。
log
2 n≤f(
n 、
k )≤n-1
「大きい」
kの場合、つまりk≥log
2 nの場合は明らかに左の境界に到達し、
k = 1の場合は右の境界に到達することがわかります
。kの中間値の場合
、検索
f (
n 、
k )不等式を満たす最小の正の整数
m (
m 0で表す):
C
m 0 + C
m 1 + C
m 2 + ... + C
m k≥n(不等式1)。
ただし、
f (
n 、
k )の真に明示的な式を取得するためにそれを解くことは、簡単な作業ではないようです。 あなたの提案を聞くのは面白いでしょう。
ただし、不等式が解決されない場合でも、目的の
m 0が位置する範囲を推定できます。これは、関数
f (
n 、
k )の値でもあります。
一般的に、提示された二項係数の和は、変数
mの次数
kの多項式と見なすことができます。 次に、不等式1から
m 0を見つけると、本質的に、多項式C
m 0 + C
m 1 + C
m 2 + ... + C
m k -
nの正の根を見つけることになります。
多項式の根を評価できるメソッドがありますが、そのためにはその係数を知る必要があり、私たちの場合、それらは怖いように見えます(折り畳まれているという事実ではない不気味な量で表されます)。 したがって、私たちは異なる行動をとります。
最初に、不等式
h 1 (
m 、
k )≤C
m 0 + C
m 1 + C
m 2 + ... +となるように、2つの関数
h 1 (
m 、
k )と
h 2 (
m 、
k )を選択します。 C
m k≤h
2 (
m 、
k )。次に、固定
kの場合、不等式
h 1 (
m 、
k )≥nおよび
h 2 (
m 、
k )≥nは簡単に解くことができます。
解
h 2 (
m 、
k )≥nは、下から目的の
m 0の推定値を与え、解
h 1 (
m 、
k )≥nは上から推定することを理解するのは簡単です。
二項係数の合計(関数
h 2 )の上限については、見つかった最良の結果は
チェルノフの不等式です:
C
m 0 + C
m 1 + C
m 2 + ... + C
m k≤
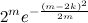
。
解決策
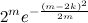
≥n
は、以下からテストの最小数の次の推定値を与えます 。
f (
n 、
k )≥
 k
k <
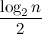
。
正直なところ、私はこの式があまり好きではありません-かさばり、「小さい」
kでのみ動作します。 しかし、それでも、常にではありませんが、最初の(粗雑な)評価よりも優れています。
一般的に、関数の値は
kの増加とともに急速に減少するため、範囲の下限はそれほど重要ではありません。
上限を明確にすることは非常に興味深いです。 これを行うには、
h 1を選択します。 二項係数の合計の下限で受け入れ可能な結果が見つかりませんでした。 何かを発明しようとする自身の試みは、面白い状況につながりました。
考えて、C
m i≥
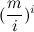
m≥i≥1の場合
後で、私は推論の間違いを見つけましたが、不平等はまだ真実であると思われ、十分なマージンがあります(数値実験で示されているように)。
不平等自体が満たされないことがさらに重要ですが、

≤C
m 0 + C
m 1 + C
m 2 + ... + C
m k 。
残念ながら、これはまだ正式には証明されていません。示唆的な考えやリンク、そしておそらく反例に感謝します。
最後に、私の仮説が真実であるという仮定に基づいて、研究を続けることにしました。したがって、結果の評価を冒険的と呼びます。
したがって、
h 1 (
m 、
k )=

。
不等式
h 1 (
m 、
k )≥nも解く必要
はありません。
mのべき乗の係数がわかっているので、多項式
h 1 (
m 、
k )
-nの根を推定できます。
マクラウリン推定値を使用する
と 、その正の根がすべて超えないことがわかります
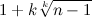
。
これは、目的の
m 0≤
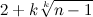
(評価2)。
私の意見では、式は非常に美しいです-コンパクトで、興味深い方法で両方の変数に依存し、最も重要なことは、範囲をうまく狭めます。
上記から
f (
n 、
k )を推定する別の方法は、
f (
n 、2)= toに制限することです。

⌉。 このフォーミュラのボールの数は考慮されていませんが、スコア2に比べてより良い結果が得られる場合があります。
確かに、
上記のテストの最小数の次の推定値を書くことができます :
f (
n 、
k )≤min {
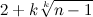
、

+ 1}。
得られた式を実際に適用すると、たとえば、
f (400、4)は9〜19の範囲にあり、実際の値は11です。さらに、範囲の右境界を与えるのは推定2であり、
f (400、2) = 28。
たとえば、
n = 2
40 、
k = 10などのより極端な値の場合、左の境界線-58、右の境界線-162を取得します。比較のために、log
2 n = 40、
f (
n 、2)= 1482910、つまり推定1、特に2は非常にうまく機能しました。 正確な値は、不等式1を解くことで見つけることができます。列挙すると、答えが76になります。
おわりに
上記のすべてを考慮すると、一般に2つのガラス玉の問題は一般に解決されていると言えます。
最小数のテストの明示的な公式はまだ得られていませんが、徹底的な検索または他の方法で不等式1を解くことにより決定できます。
公式3と4が与えられた場合、これは、簡単なアルゴリズムの操作で目的のフロアを見つけるのに十分です。
分析計算(グレード1および2)は、テストの最小数が配置される範囲を大幅に狭めることができます。これは、正確な値を計算するのに時間がかかりすぎる場合や不要な場合に役立ちます。
PS:投稿が公開されるまでに、2を評価するために使用した仮説、つまり:
C
m i≥
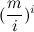
m≥i≥1の場合
したがって、評価はこれで完了です。冒険的ではありません。
同時に、二項係数またはそれらの合計の下限が考慮される文献への参照に
感謝します。
重要なUPD:問題の議論の中で、ユーザー
grechnikは二項係数の合計の下限と上限の独自のバージョンを提案しました:
h 1 (
m 、
k )=
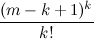
および
h 2 (
m 、
k )=
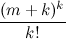
。
説明するh 1 (
m 、
k )≤C
m 0 + C
m 1 + C
m 2 + ... + C
m k≤h
2 (
m 、
k )であることを示します。 これは不等式の連鎖から得られます:
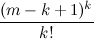
≤

= C
m k≤C
m 0 + C
m 1 + C
m 2 + ... + C
m k≤1 +
m +
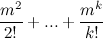
≤
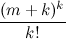
。
左側の
mのべき乗の係数は右側の係数より大きくないため、最後の不等式は真です(左側の
m lの場合、係数は

、および右側:
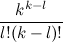
)
これで
、テストの最小数を次のように評価できます。

-k≤f(
n 、
k )≤

+
k 。
これは
、試行の
最小数が 
ボールの数に等しい数のプラス/マイナスの精度で! すごい、素晴らしい処方!
コメントでは、
grechnikと
Mrrlのユーザーは
f (
n 、
k )の値の興味深い漸近的な推定値も提供しています。