😺 🛸 ☀️ GPU SSSPの実装 🧛🏽 🚳 🎾

注釈

この記事では、SSSPアルゴリズムを効率的に並列化する方法、つまりグラフィックアクセラレータを使用してグラフ内の最短パスを見つける方法を説明します。グラフィックアクセラレータとして、ケプラーアーキテクチャのGTX Titanカードが検討されます。

はじめに

最近、グラフィックアクセラレータ（GPU）は、非グラフィックコンピューティングでますます重要な役割を果たしています。それらの使用の必要性は、それらの比較的高い生産性と低コストによるものです。ご存じのように、GPUでは、構造グリッドの問題は十分に解決されており、並列処理は簡単に区別できます。ただし、大容量を必要とし、非構造グリッドを使用するタスクがあります。このような問題の例は、単一の最短ソースパス問題（SSSP）です。これは、重み付きグラフ内の特定の頂点から他のすべての頂点までの最短パスを見つけるタスクです。 CPUでこの問題を解決するには、少なくとも2つの有名なアルゴリズム、DeystraアルゴリズムとFord-Bellmanアルゴリズムがあります。 GPUには、DeystraアルゴリズムとFord-Bellmanアルゴリズムの並列実装もあります。この問題の解決策を説明する主な記事は次のとおりです。

CUDA、Pawan Harish、PJ Narayananを使用したGPUでの大規模なグラフアルゴリズムの高速化
最短経路問題への新しいGPUベースのアプローチ、Hector Ortega-Arranz、Yuri Torres、Diego R. Llanos、およびArturo Gonzalez-Escribano

他にも英語の記事があります。しかし、これらの記事はすべて同じアプローチ、つまりDeystraアルゴリズムのアイデアを使用しています。 Ford-Bellmanアルゴリズムのアイデアとケプラーアーキテクチャの利点を使用して問題を解決する方法を説明します。 GPUのアーキテクチャと言及されたアルゴリズムについてはすでに多くのことが書かれているので、この記事ではこれについてはこれ以上書きません。また、ワープ（ワープ）、キューダブロック、SMX、およびCUDAに関連するその他の基本的な事項の概念は読者になじみがあると考えられています。

データ構造の説明

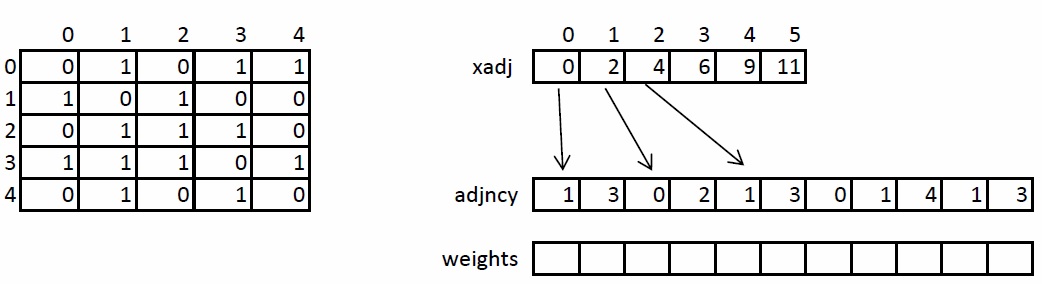
将来的に言及され、変換されるため、無向加重グラフのストレージ構造を簡単に検討します。グラフは、圧縮されたCSR形式で指定されます。この形式は、疎行列とグラフの保存に広く使用されています。 N個の頂点とM個のエッジを持つグラフの場合、xadj、adjncy、weightsの3つの配列が必要です。 xadj配列のサイズはN + 1で、他の2つは2 * Mです。これは、頂点の任意のペアの無指向グラフでは、直接アークと逆アークを格納する必要があるためです。

グラフを保存する原理は次のとおりです。頂点Iの近傍のリスト全体は、インデックスxadj [I]からxadj [I + 1]までのadjncy配列にあり、それを含みません。同様のインデックスは、頂点Iからの各エッジの重みを格納します。説明のために、左側の図は隣接行列を使用して記述された5つの頂点のグラフを示し、右側はCSR形式を示します。

アルゴリズムのGPU実装

入力準備

1つのストリーミングマルチプロセッサ（SMX）の計算負荷を増やすには、入力データを変換する必要があります。すべての変換は、2つの段階に分けることができます。

CSRフォーマットを調整してフォーマットを調整する（COO）
COO形式の並べ替え

最初の段階では、CSR形式を次のように拡張する必要があります。アークの始まりを格納する別のstartV配列を導入します。次に、adjncy配列にその両端が格納されます。したがって、近傍を保存する代わりに、アークを保存します。上記のグラフ上のこの変換の例：

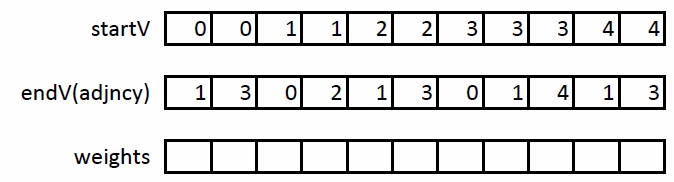
2番目の段階では、各ペア（U、V）が1回だけ発生するように、取得したエッジをソートする必要があります。したがって、エッジ（U、V）を処理する場合、GPUのグローバルメモリからこのエッジに関するデータを再読み込みする必要なく、エッジ（V、U）をすぐに処理できます。

コアコンピューティングコア

GPUでの実装の基礎は、 Ford-Bellmanアルゴリズムです。このアルゴリズムは、rib骨を互いに独立して表示でき、rib骨のデータとその重みが一列に並んでいるため、GPUメモリの帯域幅が向上するため、GPUでの実装に適しています。

int k = blockIdx.x * blockDim.x + threadIdx.x; if(k < maxV) { double w = weights[k]; unsigned en = endV[k]; unsigned st = startV[k]; if(dist[st] > dist[en] + w) // (*) { dist[st] = dist[en] + w; modif[0] = iter; } else if(dist[en] > dist[st] + w) // (**) { dist[en] = dist[st] + w; modif[0] = iter; } }

このカーネルでは、各スレッドが2つのエッジ（順方向と逆方向）を処理し、それらの1つに沿った距離を改善しようとします。 ifブロックの両方の条件を同時に満たすことができないことは明らかです。各エッジが順番にスキャンされるFord-Bellmanアルゴリズムとは異なり、GPUで実装されたアルゴリズムでは、2つ以上のフローが同じdist [I]セルを更新するときにフローの「競合」の状況が発生する場合があります。この場合、アルゴリズムは正しいままであることを示します。

cell dist [I]を更新する2つのスレッドK1およびK2があるとします。これは、条件（*）または（**）が満たされることを意味します。 2つのケースが考えられます。最初-2つのスレッドのうちの1つが最小値を記録しました。次に、これら2つのスレッドの次の反復で条件はfalseになり、セルdist [I]の値は最小になります。 2番目-記録された2つのスレッドの1つは最小値ではありません。その後、次の反復で、条件はスレッドの1つに対してtrue、他のスレッドに対してfalseになります。したがって、結果は両方のケースで同じになりますが、異なる反復回数で達成されます。

Ford-Bellmanアルゴリズムの最適化されたバージョンによれば、反復でdist配列に変更がなかった場合、それ以上の反復は意味がありません。 modif変数はこれらの目的のためにGPUに導入され、スレッドは現在の反復の数を書き込みました。

1回の反復-1回のカーネル起動。基本バージョンでは、CPUでループでカーネルを開始し、modif変数を読み取ります。前回の反復から変更されていない場合、dist配列では、問題に対する答えは、指定された頂点から他のすべての頂点への最短パスです。

実装されたアルゴリズムの最適化

次に、アルゴリズムのパフォーマンスを大幅に改善できる最適化を検討します。最終的なアーキテクチャの知識は、最適化の実行に役立ちます。

最新のCPUには3レベルのキャッシュがあります。一次キャッシュのサイズは64Kで、すべてのプロセッサコアに含まれています。 2次キャッシュのサイズは1〜2MBです。第3レベルのキャッシュはCPU全体に共通であり、サイズは12〜15MB程度です。

最新のGPUには2レベルのキャッシュがあります。一次キャッシュのサイズは64KBです。共有メモリとレジスタの混雑に使用されます。共有メモリに使用できるのは48KB以下です。各コンピューティングユニットに含まれています。 2次キャッシュの最大サイズは1.5 MBで、GPU全体に共通です。 GPUのグローバルメモリからダウンロードされたデータをキャッシュするために使用されます。最新のGPU GK110チップには15の処理ユニットがあります。約48KBの第1レベルキャッシュと102KBの第2レベルキャッシュが1つのブロックに収まることがわかります。 CPUと比較すると、これは非常に小さいため、GPUのグローバルメモリからの読み取り操作は、中央処理装置のメインメモリからの読み取り操作よりも高価です。また、Keplerアーキテクチャには、読み取り専用のテクスチャキャッシュに直接アクセスする機能があります。これを行うには、カーネルの対応する仮パラメータの前にconst __restrictを追加します。

テクスチャキャッシュを使用する

このタスクでは、距離のdist配列を常に更新して読み取る必要があります。この配列は、アークとその重みに関する情報と比較して、GPUのグローバルメモリでかなりのスペースを占有します。たとえば、頂点数が2 ²⁰ （約100万）のグラフの場合、dist配列は8 MBを占有します。それにもかかわらず、この配列へのアクセスはランダムに実行されます。これは、グローバルメモリから各コンピューティングワープへの追加のダウンロードが生成されるため、GPUにとっては不適切です。ワープごとのダウンロード数を最小限に抑えるために、L2キャッシュにデータを保存し、読み取りますが、他のワープデータでは使用しません。

テクスチャキャッシュは読み取り専用であるため、それを使用するには、dist距離の同じ配列に2つの異なるリンクを入力する必要がありました。関連コード：

 __global__ void relax_ker (const double * __restrict dist, double *dist1, … …) { int k = blockIdx.x * blockDim.x + threadIdx.x + minV; if(k < maxV) { double w = weights[k]; unsigned en = endV[k]; unsigned st = startV[k]; if(dist[st] > dist[en] + w) { dist1[st] = dist[en] + w; modif[0] = iter; } else if(dist[en] > dist[st] + w) { dist1[en] = dist[st] + w; modif[0] = iter; } } }

その結果、カーネル内ではすべての読み取り操作が1つのアレイで実行され、すべての書き込み操作が別のアレイで実行されることが判明しました。ただし、distとdist1の両方のリンクは、同じGPUメモリの場所を指します。

キャッシュ使用率を向上させるデータのローカライズ

上記の最適化の最高のパフォーマンスを得るには、ダウンロードされたデータが可能な限りL2キャッシュにあることが必要です。 dist配列は、endVおよびstartV配列に格納されている事前定義されたインデックスを使用してアクセスされます。呼び出しをローカライズするために、dist配列を特定の長さのセグメント（P要素など）に分割します。グラフにはN個の頂点があるため、（N / P + 1）個の異なるセグメントを取得します。次に、次のようにエッジをこれらのセグメントにソートします。最初のグループでは、端がゼロセグメントに含まれるエッジと、最初にゼロのエッジ、次に最初のセグメントなどのエッジを割り当てます。 2番目のグループでは、端が最初のセグメントに属し、端が最初にゼロに、次に最初に、などのエッジを割り当てます。

このエッジの置換後、最初のグループのスレッドが終了頂点とゼロ、最初などのゼロセグメントからデータを要求する限り、たとえば最初のグループに対応するdist配列の要素の値はキャッシュ内にあります。開始頂点のため。さらに、スレッドが3つ以下の異なるセグメントからデータを要求するように、エッジが配置されます。

アルゴリズムのテスト結果

テストには、非指向性の合成RMATグラフを使用しました。これは、ソーシャルネットワークとインターネットからの実際のグラフをうまくモデル化したものです。グラフの平均接続性は32で、頂点の数は2の累乗です。次の表に、テストされたグラフを示します。

頂点の数2 ^ N	頂点の数	アークの数	dist配列のサイズ（MB）	rib骨の配列のサイズと重量（MB）
14	16 384	524,288	0.125	4
15	32,768	1,048,576	0.250	8
16	65,536	2,097 152	0,500	16
17	131 072	4 194 304	1	32
18	262 144	8 388 608	2	64
19	524,288	16 777 216	4	128
20	1,048,576	33554432	8	256
21	2,097 152	67108864	16	512
22	4 194 304	134 217 728	32	1024
23	8 388 608	268 435 456	64	2048
24	16 777 216	536 870 912	128	4096

表から、頂点数が2 ¹⁸以上のグラフの距離配列distは、GPUのL2キャッシュに完全には収まらないことがわかります。テストは、192個（合計2688個）のcudaコアを備えた14個のSMXと、周波数3.4GHzおよび8MBキャッシュを備えた第3世代Intelコアi7プロセッサーを備えたNividia GTX Titan GPUで実行されました。 CPUのパフォーマンスを比較するために、最適化されたダイクストラアルゴリズムが使用されました。 CPUで作業する前のデータ置換の形での最適化は行われませんでした。時間ではなく、パフォーマンスインジケータは、1秒あたりに処理されるアークの数です。この場合、取得した時間をグラフ内のアークの数で割る必要があります。最終結果として、平均32ポイントが取得されました。最大値と最小値も計算されました。

コンパイルには、13番目のバージョンのIntelコンパイラと、フラグ–O3 –arch = sm_35を使用したNVCC CUDA 5.5が使用されました。

完了した作業の結果として、次のグラフを検討してください。

このグラフは、次のアルゴリズムの平均パフォーマンス曲線を示しています。

キャッシュ&&制限-すべての最適化を備えたGPUアルゴリズム
キャッシュオフ-キャッシュを改善するために順列を最適化しないGPUアルゴリズム
制限-テクスチャキャッシュの最適化なしのGPUアルゴリズム
キャッシュ&&制限オフ-最適化なしの基本的なGPUアルゴリズム
CPU-CPUの基本アルゴリズム

両方の最適化がパフォーマンスに大きく影響することがわかります。 const __restrict最適化を誤用するとパフォーマンスが低下する可能性があることに注意してください。結果の加速度はこのグラフで見ることができます：

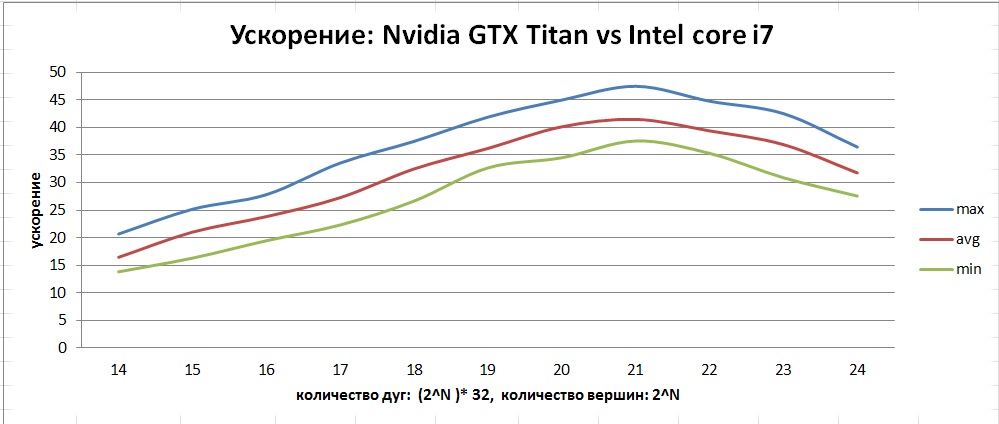
このグラフは、CPUとは異なり、GPUの平均からの偏差の範囲が広いことを示しています。これは、フローの「レース」の形式でのアルゴリズム実装の特性によるものです。なぜなら、最初から最初まで、異なる反復回数を取得できるからです。

おわりに

行われた作業の結果、SSSPアルゴリズムが開発、実装、および最適化されました-グラフ内の最短パスの検索。このアルゴリズムは、特定の頂点から他のすべての頂点までのグラフ内の最短距離を検索します。 GTX Titanメモリに収まるすべてのグラフの中で、最大パフォーマンスは、頂点数が最大^21のグラフで示されています-1秒あたり約1億のエッジ。達成された最大平均加速度は、頂点の数が100万から400万のグラフで約40でした。

GPU SSSPの実装

注釈