O（n）複雑度のBitSortingアルゴリズム

背景

空き時間に、彼は複雑さO（n）を持つサイジングアルゴリズムを作成して、追加のメモリを大量に消費せず、簡単に並列化できるかどうかを検討することにしました。 そして彼はいくつかの結果を達成しました。

次の数字のセットがあると想像してください。

• 123
• 12345
• 22345
• 12345678
• 1

人間として、このデータ配列をどのようにソートしますか？ そうです、最も視覚的に長い番号を選択します。
そして、長さが同じ場合、1つのカテゴリの数値を比較します。 コンピューターを機能させることもできると思いました。

アルゴリズム

したがって、入力にはサイズNの数値の配列があります。

int[] array = new int[n] 

次に、配列の各要素をバイナリ形式で表し、新しいリストに保存します。

 bool[][] bitMatrix = new bool[n][]; //    for (int i = 0; i < array.Length; i++) { BitArray bitArray = new BitArray (new int[1]{ array [i] }); bool[] bits = new bool[bitArray.Length]; bitArray.CopyTo (bits, 0); Array.Reverse (bits); bitMatrix [i] = bits; } 

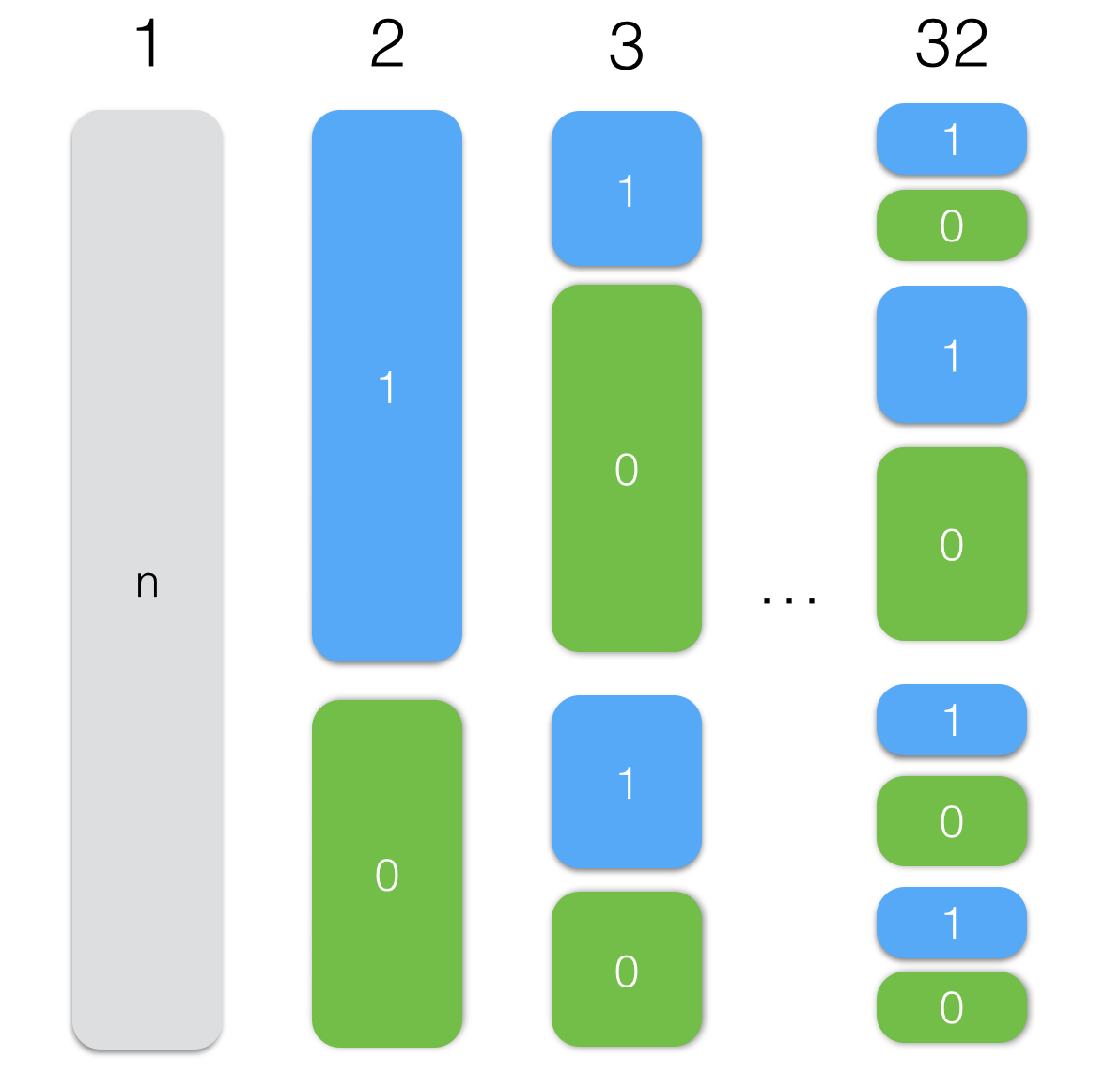
次のマトリックスが得られました。


次に、最も興味深い部分が来ます：再帰的ソート。
はじめに、このビットマトリックスをどのように並べ替えるかを見てみましょう。

1. 最初の列を見る
2. 1つのリストで最初のビットが1であるすべての要素を選択します
3. 2番目のリストで最初のビットが0であるすべての要素を選択します
4. 最初のリストと2番目のリストについて手順2と3を繰り返しますが、すでに列番号2

コードは次のようになります。

 private void SortAlgorithm(bool[][] bitMatrix, int columnNumber) { List<bool[]> ones = new List<bool[]> (); List<bool[]> zeros = new List<bool[]> (); for (int i = 0; i < bitMatrix.Length; i++) { if (bitMatrix[i][columnNumber]) ones.Add(bitMatrix[i]); else zeros.Add(bitMatrix[i]); } columnNumber++; if (columnNumber == MAX_COLUMN_COUNT)//MAX_COLUMN_COUNT = sizeof(int)*8 { sortedBitMatrix.AddRange(ones); sortedBitMatrix.AddRange(zeros); return; } if (ones.Count != 0) SortAlgorithm (ones.ToArray(), columnNumber); if (zeros.Count != 0) SortAlgorithm (zeros.ToArray(), columnNumber); } 

sortBitMatrixは 、ソートされたビット行列を格納するために使用されます。
ビット行列を変換して配列に戻すには、次の方法を使用します。

 private int[] ConvertBitMatrixToArray(List<bool[]> bitMatrix) { int[] resultArray = new int[bitMatrix.Count]; int count = 0; for (int i = 0; i < bitMatrix.Count; i++) { bool[] bits = bitMatrix [i]; Array.Reverse(bits); BitArray bitArray = new BitArray(bits); int[] tmpArray = new int[1]; bitArray.CopyTo(tmpArray, 0); resultArray [count] = tmpArray [0]; count++; } return resultArray; } 

メソッドの結果は、ソートされた配列になります。

しかし、並列化はどうでしょうか？

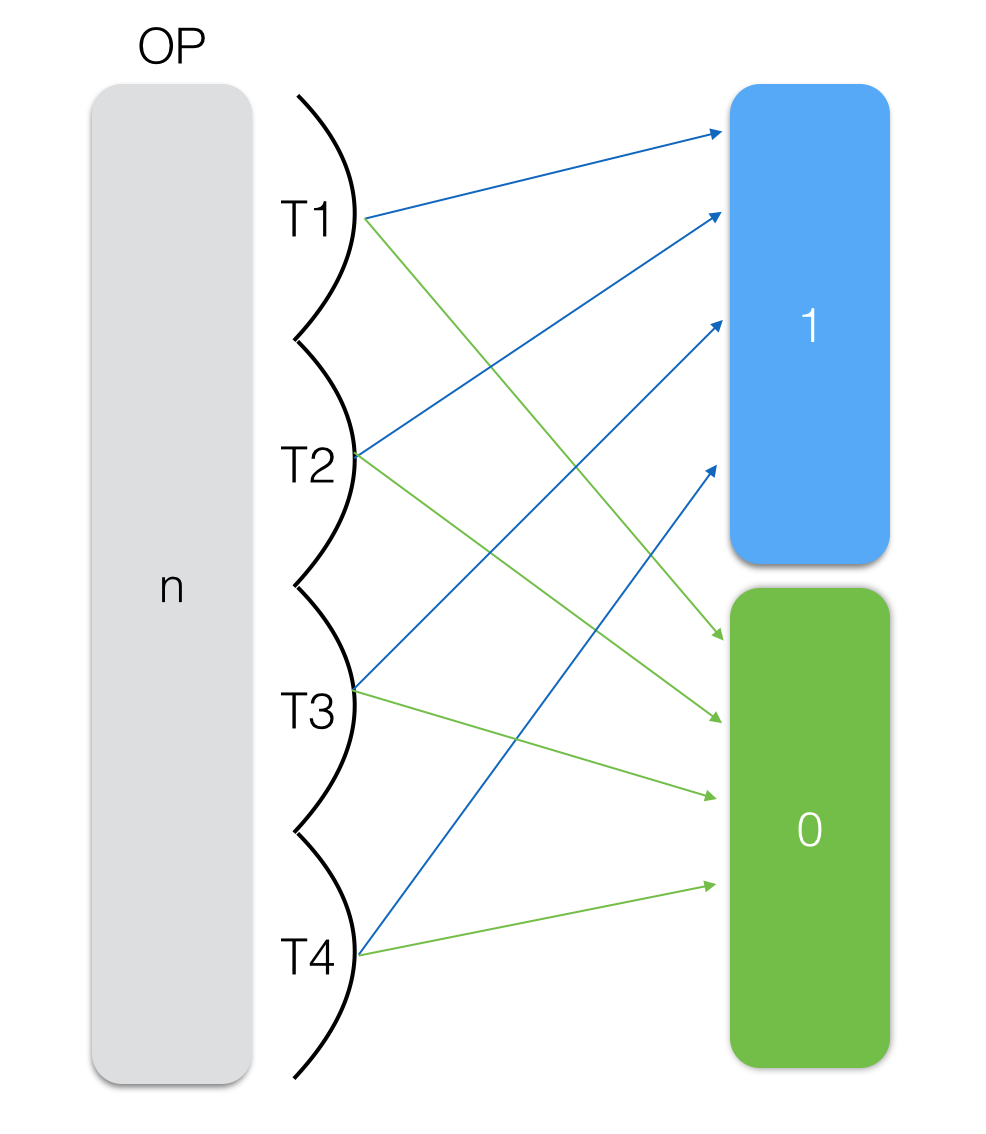
ほとんどの時間は1と0の検索でビットマトリックスの各列を通過するために費やされるため、このプロセスは複数のスレッドで開始できます。
各スレッドは、マトリックス部分で1と0を探します。

難易度

特定の配列をソートするには、次の反復が必要です。

1. ビット行列の作成：n
2. 0と1を検索：32n
3. ソート済みビットマトリックスの変換：n

合計：34n、O（n）

あなたの意見は興味深いです。
ご清聴ありがとうございました。

PS github.com/koljaka/BitSorting