
こんにちは、読者。
ランダムフォレストは現在、分類や回帰などの機械学習の問題を解決するための最も一般的で非常に効果的な方法の1つです。 効率の面では、参照ベクトルマシン、ニューラルネットワーク、ブースティングと競合しますが、欠点がないわけではありません。 見た目では、学習アルゴリズムは非常にシンプルです(人生でスリルがほとんどないサポートベクターマシンの学習アルゴリズムと比較して、余暇にこれを行うことを強くお勧めします)。 ランダムフォレストに固有の主なアイデア(バイナリデシジョンツリー、ブートストラップ集約またはバギング、ランダムサブスペースメソッドおよび非相関)をアクセス可能な形式で理解し、これらすべてが連携する理由を理解しようとします。 競合他社に関するモデルはまだかなり若いです。
1997年に 、新しいツリーノードを作成するときに属性のランダムな部分空間を使用して単一の決定ツリーを構築する方法を著者が提案した
記事から始まりました。 その後、一連の記事があり
、2001年にアルゴリズムの標準バージョンが公開され、ブートストラップ集約またはバギングに基づいて決定木のアンサンブルが構築されました。 最後に、このモデルをc#で実装するための簡単な、まったく迅速な方法ではなく、非常に視覚的な方法と一連のテストを提供します。 ちなみに、
右側の
写真では、ここで
クロニアンスピットのカリーニングラード地域に生えている真にランダムな森を見ることができます。
バイナリ決定木
フォレストの主要な構造要素と同様に、ツリーから開始する必要がありますが、検討中のモデルのコンテキストで行います。 プレゼンテーションは読者が
木がデータ構造としてどんなものであるかを理解するという仮定に基づくでしょう。 ツリーは、バイナリ決定ツリーを構築
するCART (分類および回帰ツリー)
アルゴリズムに従って
ほぼ構築されます。 ところで、ここハブには、
エントロピーの最小化に基づいたそのような
ツリーの構築に関する適切な記事があります。このバージョンでは、これは特別なケースになります。 2次元の標識のスペースを想像してみてください。そうすると、視覚化が容易になり、2つのクラスの多くのオブジェクトが与えられます。

いくつかの表記法を紹介します。 機能のセットを次のように示します。
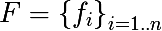
各機能について、トレーニングセットに基づいて、または問題に関する他のアプリオリ情報を使用して、値のセットを区別できます。属性の値の有限セットを次のように示します。
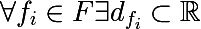
ラベルに関するセットの
不均一性のいわゆる尺度を導入することも必要です。 トレーニングセットのサブセットが
5つの赤と
10の青のオブジェクトで構成されていると想像してください。このサブセットでは、赤のオブジェクトが伸びる確率は
1/3で、青は
2/3になると言えます。 次のように、トレーニングセットの一部のサブセットにおけるk番目のクラスの確率を示します。
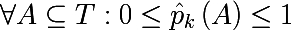
したがって、観測のサブセットにおけるラベルの経験的離散確率分布を定義しました。 このサブセットの
不均一性の尺度は、次の形式の関数と呼ばれます。ここで、
K(A)はサブセット
Aのラベルの総数です。
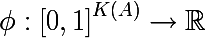
不均一性の尺度は、関数の値がセットの不均一性の増加に応じて可能な限り増加するように設定され、セットがすべての種類のラベルの同じ数で構成される場合に最大になり、セットが同じクラスのラベルのみで構成される場合に最小になります(参照することをお勧めします
写真付きのエントロピーの例 )。
不均一性の尺度のいくつかの例を見てみましょう(ベクトル
pは
、トレーニングセットのサブセット
Aで発生するラベルの
m確率で構成されます)。
二分決定木を構築するためのアルゴリズムは、
欲張りアルゴリズムに従って動作し
ます 。各反復で、トレーニングセットの入力サブセットについて、そのような空間のパーティションは、取得した2つのサブセットの不均一性の平均尺度を最小化する超平面(座標軸の1つに直交)によって構築されます。 この手順は、停止条件が満たされるまで、受信した各サブセットに対して再帰的に実行されます。 これをより正式に記述します。入力セット
Aに対して、<
sign 、
sign value >のペアを見つけ、不均一性の尺度が最小になるようにします。
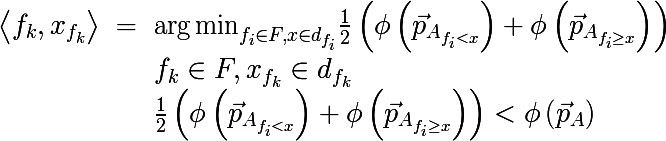
どこで
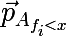
条件
f <xが満たされる要素で構成される集合
Aのサブセットから上記の手順で取得される確率ベクトルです。 また、パーティションの平均コストが元のセットのコストを超えないことを忘れないでください。 元の画像に戻って、実際に何が起こるかを見て、上記の方法で元のデータセットを分割しましょう。
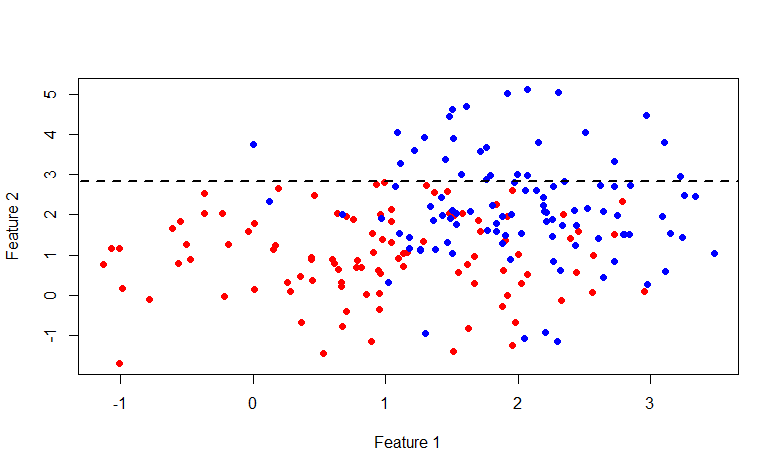
ご覧のとおり、行
y = 2.840789の上のセットは完全に青いラベルで構成されているため、2番目のセットのみを分解するのが理にかなっています。
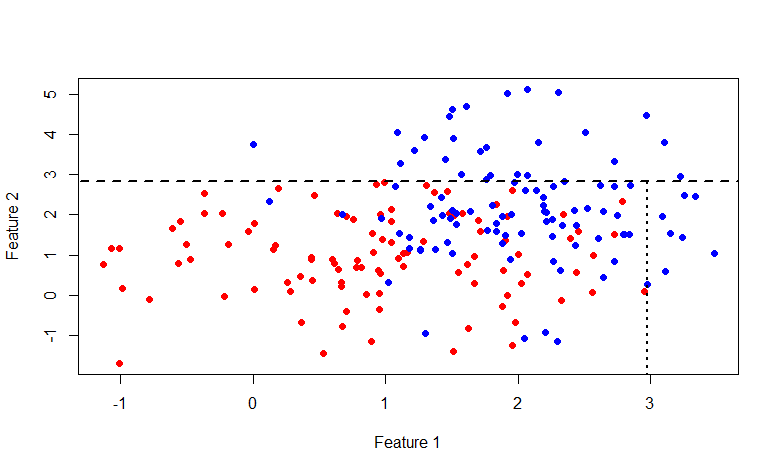
今回は、行
x = 2.976719です。 一般的に、この写真にふけることに興味がある人は誰でも、ここにRコードがあります。
可視化コードrm(list=ls()) library(mvtnorm) labCount <- 100 lab1 <- rmvnorm(n=labCount, mean=c(1,1), sigma=diag(c(1, 1))) lab0 <- rmvnorm(n=labCount, mean=c(2,2), sigma=diag(c(0.5, 2))) df <- data.frame(x=append(lab1[, 1], lab0[, 1]), y=append(lab1[, 2], lab0[, 2]), lab=append(rep(1, labCount), rep(0, labCount))) plot(df$x, df$y, col=append(rep("red", labCount), rep("blue", labCount)), pch=19, xlab="Feature 1", ylab="Feature 2") giniIdx <- function(data) { p1 <- sum(data$lab == 1)/length(data$lab) p0 <- sum(data$lab == 0)/length(data$lab) return(p0*(1 - p0) + p1*(1 - p1)) } p.norm <- giniIdx getSeparator <- function(data) { idx <- NA idx.val <- NA cost <- p.norm(data) for(i in 1:(dim(data)[2] - 1)) { for(i.val in unique(data[, i])) { #print(paste("i = ", i, "; v = ", i.val, sep="")) cost.tmp <- 0.5*(p.norm(data[data[, i] < i.val, ]) + p.norm(data[data[, i] >= i.val, ])) if(is.nan(cost.tmp)) { next } if(cost.tmp < cost) { cost <- cost.tmp idx <- i idx.val <- i.val } } } return(c(idx, idx.val)) } s1 <- getSeparator(df) lines(c(-100, 100), c(s1[2], s1[2]), lty=2, lwd=2, type="l")
可能な停止基準をリストします。最大ノード深度に達しました。 パーティション内の支配的なクラスの確率が特定のしきい値を超えています(0.95を使用)。 サブセット内の要素の数が特定のしきい値未満です。 その結果、セット全体のパーティションを(ハイパー)長方形に分割し、そのようなトレーニングセットの各サブセットはツリーの1つのリーフに関連付けられ、すべての内部ノードはパーティションの条件の1つです。 または言い換えれば、いくつかの述語。 現在のノードでは、左側の子は、述語がtrueであるセットの要素に関連付けられ、右側の子は、述語がfalseを返すサブジェクトにそれぞれ関連付けられます。 次のようになります。

それで、私たちは木を手に入れました。 特定の決定木に従って、トレーニングセットのどのサブセットが入力画像に属しているかを判断することは難しくありません。 次に、このサブセットの支配的なクラスのみを選択してクライアントに返すか、このサブセットのラベルの確率分布を返すことができます。
ところで、
回帰問題を犠牲にして。 説明されているツリーの構築方法は、分類問題から回帰タスクに簡単に変更できます。 このためには、不均一性の尺度を、予測誤差の尺度(標準偏差など)に置き換える必要があります。 そして、決定を行う際に、支配的なクラスの代わりに、ターゲット変数の平均値が使用されます。
すべては木で決定されたようです。 この方法の長所と短所については説明しません;
Wikipediaに良いリストがあります。 しかし、最終的には、線形モデルとツリーの違いについて、
統計学習の概要から図を追加します。
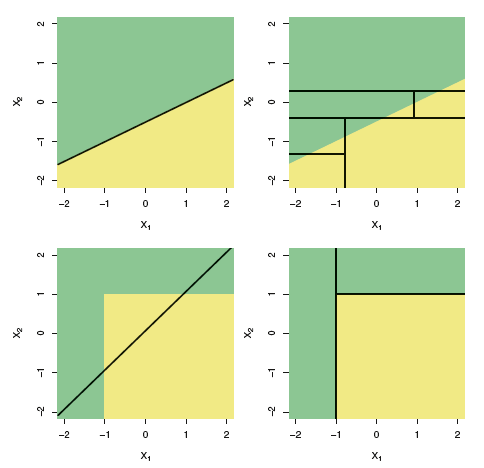
この図は、線形分離性の場合に見られるように、線形モデルとバイナリ決定ツリーの違いを示しています。一般に、ツリーは単純な線形分類器よりも精度の低い結果を示します。
ブートストラップの集約またはバギング
ランダムフォレストの次のイデオロギー要素に進みましょう。 したがって、
BAG gingという名前は、
B ootstrap
AGの集約に由来しています。 統計では、ブートストラップは、サンプル確率分布の統計の標準誤差を推定する方法と、
モンテカルロ法に基づいてデータセットからサンプルを
サンプリングする方法の両方を意味すると理解されています。
ブートストラップサンプリングは、そのアイデアが非常に単純であり、実際の分布から多数のサンプルを取得できない場合に使用されます。これはほとんどの場合に当てはまります。 サイズ
nの m個の観測セットを取得したいが、自由に使える
n個の観測セットは1つだけであるとします。 次に、元のセットから
n個の要素を等
確率で選択して
m個のセットを生成し、選択した要素を返します(
繰り返しまたはreturnでサンプリングします)。
nの値が大きい場合、ブートストラップによってセットをサンプリングすることによって取得される一意の要素の数は、
(1-1 / e)≈初期セットの一意の観測の総数の
63.2%になります。 サンプリングによるブートストラップによって得られた
i番目のセットを
D iとし、そのパラメータ
a iを評価
し 、この手順を
m回繰り返します。 標準エラーブートストラップパラメーターの推定値は次のように記述されます。
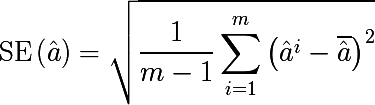
そのため、
統計ブートストラップを使用すると、いくつかの分布パラメーターの推定におけるエラーを評価できます。 しかし、これはトピックからの気を散らすものですが、ブートストラップのサンプリング方法に興味があります。
ここで、1つの確率分布から、ランダムに選択された
m個の独立した要素
xのセットを、数学的期待値と分散
σ2で検討します。 サンプルの平均は次のようになります。
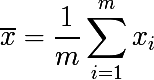
サンプル平均は、平均や分散とは異なり、分布パラメーターではなく、ランダム変数の関数です。 また、標本平均の確率分布から得られる確率変数です。 そして、次のように表現される分散パラメーターがあります。
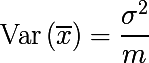 ランダム変数の値のセット
ランダム変数の値のセットを
平均すると、ばらつきが減少することがわかります。 これは、ブートストラップサンプルを集約するという考え方の基礎です。 トレーニングセット
D (サイズ
nも )からサイズ
nの m個のブートストラップサンプルを生成します。
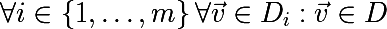
各ブートストラップサンプルで、
fモデルをトレーニングし、次の関数を導入します。このアプローチは、ブートストラップの集約またはバギングと呼ばれます。
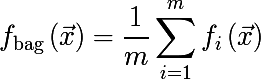
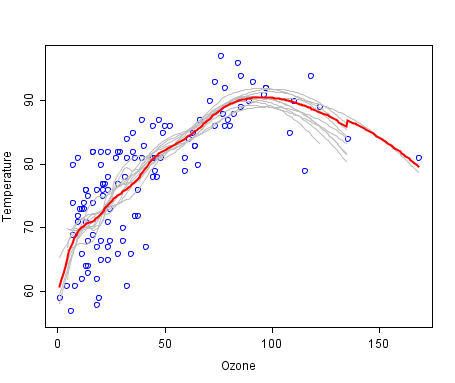
バギングは
、Wikipediaの
次のグラフで説明できます。ここでは、バッグモデルは赤線で示されており、他の多くのモデルの平均です。
脱相関
フォレストを取得する方法は既に明確になっていると思います。ブートストラップサンプルを多数生成し、それぞれについて決定ツリーをトレーニングします。 しかし、小さな問題があります。ほとんどすべての木はほぼ同じ構造になります。 実験を行い、
2つのクラスと32の特徴を持つ
セットを取り、ブートストラップサンプルで1000の決定木を構築し、ルートノードの述語の変動性を見てみましょう。
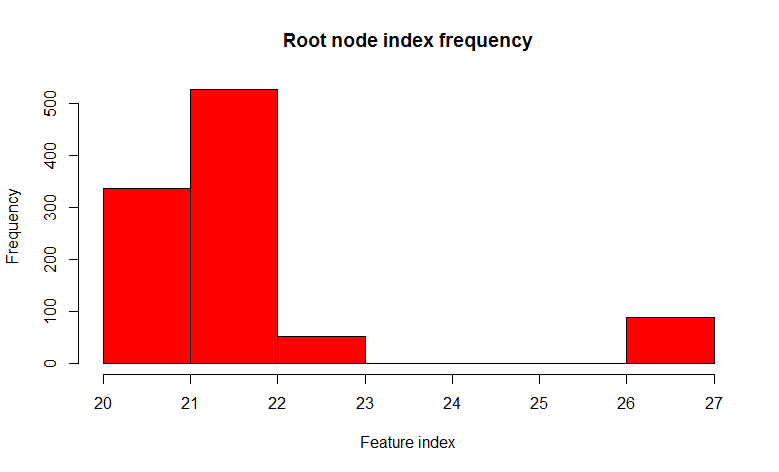
1000本のツリーのうち、22番目のサイン(明らかにフィーチャの値が同じ)は526本のツリーで見つかり、ほとんどすべてのドーターノードで同じであることがわかります。 つまり、ツリーは
相互に相関しています。 ほんの数個、多くの場合1つまたは2つで十分であれば、1000本の木を構築することは意味がないことがわかります。 そして今、ツリーを構築するとき、各ノードを分割するとき、すべての記号のセットからいくつかの小さなランダムな記号のセット、たとえば32のうち7つのランダムを使用してみましょう。
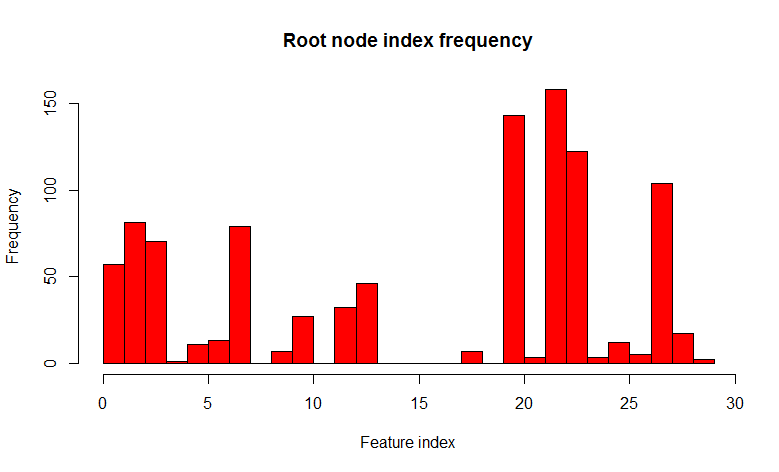
ご覧のとおり、分布は多種多様なツリーの方向に大きく変化しています(ところで、ルートノードだけでなく、ドーターノードでも)、これがそのようなトリックの目的でした。 現在、158の場合にのみ22の兆候が見つかります。 「
32個の標識の
うち7個のランダム 」の選択は、経験的観察(この観察の著者は見つかりませんでした)によって正当化され、分類問題では通常これは標識の総数の平方根です。 言い換えれば、ツリーの
相関性が低くなり、プロセスは
非相関と呼ばれます。
一般に、このような方法は
ランダム部分空間法と呼ばれ、決定木だけでなく、ニューラルネットワークなどの他のモデルにも使用されます。
一般的に、このようなものは普通の平らな森のように見え、装飾されていません。

コード
実装に移りましょう。 繰り返しになりますが、ここで紹介した例はランダムフォレストの簡単な実装ではなく、本質的に教育的なものであり、モデルの主要なアイデアを理解できるように設計されています。 たとえば、
ここでは適切で機敏な実装の例を見つけることができますが 、残念ながらあまり明確ではありません。
クラスを断片に分割しないように、必要に応じてコードに直接コメントを挿入します。
私の場合の観測単位は、次のクラスで表されます。
観察 public class DataItem<T> { private T[] _input = null; private T[] _output = null; public DataItem() { } public DataItem(T[] input, T[] output) { _input = input; _output = output; } public T[] Input { get { return _input; } set { _input = value; } } public T[] Output { get { return _output; } set { _output = value; } } }
ツリーの各ノードについて、分類の決定に使用される述語に関する情報を保存する必要があります。
ツリーノードデータ public class ClassificationTreeNodeData {
二分決定木のクラスを考えてみましょう。
バイナリ決定木 public class ClassificationBinaryTree { private TreeNode<ClassificationTreeNodeData> _rootNode = null; private INorm<double> _norm = null;
決定木のクラスで使用される
標準について詳しく見てみましょう。
レートインターフェイス public interface INorm<T> { double Calculate(T[] v); }
ジニ指数 internal class GiniIndex : INorm<double> { #region INorm<double> Members public double Calculate(double[] v) { return v.Sum(p => p*(1 - p)); } #endregion }
クロスエントロピー internal class MetricsBasedNorm<T> : INorm<T> { private IMetrics<T> _m = null; internal MetricsBasedNorm(IMetrics<T> m) { _m = m; } #region INorm<T> Members public double Calculate(T[] v) { return _m.Calculate(v, v); } #endregion } public interface IMetrics<T> { /// <summary> /// Calculate value of metrics /// </summary> double Calculate(T[] v1, T[] v2); /// <summary> /// Get centroid/clusteroid of data /// </summary> T[] GetCentroid(IList<T[]> data); /// <summary> /// Calculate value of partial derivative by v2[v2Index] /// </summary> T CalculatePartialDerivaitveByV2Index(T[] v1, T[] v2, int v2Index); } internal class CrossEntropy : MetricsBase<double> { internal CrossEntropy() { } /// <summary> /// \sum_i v1_i * ln(v2_i) /// </summary> public override double Calculate(double[] v1, double[] v2) { if (v1.Length != v2.Length) { throw new ArgumentException("Length of v1 and v2 should be equal"); } if (v1.Length == 0 || v2.Length == 0) { throw new ArgumentException("Vector dimension can't be 0"); } double d = 0; for (int i = 0; i < v1.Length; i++) { d += v1[i]*Math.Log(v2[i] + Double.Epsilon); } return -d; } public override double CalculatePartialDerivaitveByV2Index(double[] v1, double[] v2, int v2Index) { return v2[v2Index] - v1[v2Index]; } }
さて、ランダムフォレストクラスのみを考慮することは残っています。
ランダムフォレスト public class ClassificationRandomForest {
結論と参考文献
コードを調べると、ツリー内に構造と条件を
ドット形式に書き込むための関数があり、
GraphVisによって視覚化されていることがわかります。
上記のセットで次のパラメーターを使用
してランダムフォレストを実行する場合:
ClassificationRandomForest crf = new ClassificationRandomForest( NormCreator.CreateByMetrics(MetricsCreator.CrossEntropy()), 10, 1, null, Convert.ToInt32(Math.Round(Math.Sqrt(ds.TrainSet.First().Input.Length))), 0.95, 1000, true ); crf.Train(ds.TrainSet);
次のコードは、このフォレストを視覚化するのに役立ちます。
foreach (ClassificationBinaryTree tree in crf.Forest) { using (StreamWriter sw = new StreamWriter(@"e:\Neuroximator\NetworkTrainingOCR\TreeTestData\Forest\" + (new DirectoryInfo(@"e:\Neuroximator\NetworkTrainingOCR\TreeTestData\Forest\")).GetFiles().Count() + ".dot")) { tree.WriteDotFile(sw); sw.Close(); } }
dot.exe -Tpng "tree.dot" -o "tree.png"
それらのいくつかを見てみましょう、彼らは無相関のために完全に異なっています。
そして最後に、いくつかの便利なリンク: