ダミーの差分暗号解析

FEALコードの強度はDESと同じです。 さらに、キーの長さの増加（DESの56ビットと比較して64ビット）により、列挙が困難になります。 FEAL暗号には、ランダムに近い暗号テキストの良好な分布があります。 また、DESと比較してFEALを支持しています。

これは、1987年のFEAL暗号化アルゴリズム仕様の要約です。

永遠に続くものはありません。 このトピックでは、オープンクローズテキストが40ペアしかない場合に、数分で完全なFEAL4キーを取得する方法を説明します。

差分暗号解読

まず、ロシアの耳を愛careする「差分暗号解析」という名前の下に隠されているものを把握しましょう。
差分暗号解読は、選択されたクリアテキストによる攻撃です。 これは、DCを使用するために、絶対にあらゆる量のテキストを絶対に暗号化できる必要があることを意味します。

DCを使用する攻撃者の目標は、キーに関する情報を取得することです。これにより、キーが完全に侵害され（非常にまれ）、キーを選択する際に何らかの利点が得られます。

すべて次のように機能します。 2つの事前に選択された暗号文P ₁およびP _{2について、}攻撃者は「差分」ΔP= P 1⊕P _2を計算します。 そして、ΔPの助けを借りて、彼はΔ= C 1⊕C2の暗号文の「差分」がどうあるべきかを決定しようとしています。 多くの場合、Δの値を100％の精度で予測することは不可能です。 攻撃者ができる唯一のことは、暗号が所定のΔPに対してさまざまなΔ値を返す頻度を決定することです。 この知識により、攻撃者はキーの一部またはキー全体を開くことができます。

例として、次の図に示す3ラウンドブロック暗号を見てみましょう。

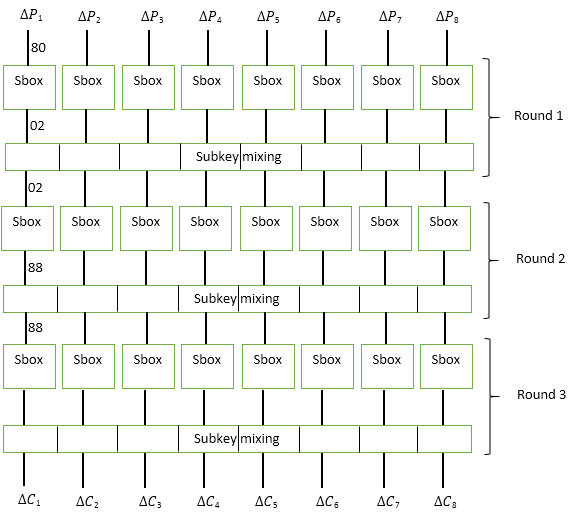
この暗号には、64ビットのブロックサイズと128ビットのキーがあります。
各ラウンドで、入力ブロックは8バイトに分割され、各バイトはSbox置換関数を通過します 。 その後、データは64ビットのサブキーサブキーと混合されます。 シャッフル機能は通常のXORです。

攻撃者が差分0x80を確認することにしたと仮定します。 これを行うために、任意のバイトX _1を生成し、X ₂ = X 1⊕80を計算します。
次に、攻撃者はSbox関数を介してX ₁とX ₂を実行し、Y ₁とY _2の値を受け取ります。 差分が80であるこのようなペアX ₁およびX ₂ごとに、攻撃者は差分ΔYを取得できます。 攻撃者は、取得した値を分析して、発生する可能性が高いΔY値を選択します。

例に戻って、すべての256のペアX ₁とX _2のうち、192の場合Y 1⊕Y ₂ = 02と仮定します。 したがって、特定のΔX= 80の場合、値ΔY= 02の確率は192/256 = 3/4です。 これは、順番に、与えられたΔX= 80に対して、確率P ₁ = 3/4で、2つの値U ₁とU _2が 、ΔU= 02のように、第2ラウンドの入力に到達することを意味します。
キーが差分の値に影響することは決してないことに注意してください。 異なるテキストを暗号化し、XORを使用してキーシーケンスと混合する場合、キーは変更されないため、ΔUを計算する場合、キーのバイトは相互に除外されます。

2回目のラウンドの特性を明らかにするために、攻撃者は入力バイトX ₁とX _2の新しい256ペアを生成します（X 1⊕X ₂ = 02）。 X ₁とX _2の各ペアのSbox関数を計算した後、攻撃者は256のΔY= 88のうち64の場合に気づきます。 つまり 与えられたΔX= 02に対してΔY= 88である確率は、P ₂ = 64/256 = 1/4です。

したがって、攻撃者は確率の簡単な計算を行って、バイトX ₁とX _2の各ペアの指定された暗号について、ΔX= 80、確率P = P ₁ * P ₂ = 3/4 * 1/4 = 3であることを理解します/ 16、最後のラウンドの前の暗号の内部状態の差分はΔY= 88です。

この知識を所有している攻撃者は、ΔP= 808080808080となるテキストのペアをいくつか生成し、3番目のサブキーのバイト単位の選択に進みます。
サブキーの最初のバイトを開く方法を示します。
最初のサブキーバイト[0]の256個の可能なバリアントのそれぞれと、暗号文ペア{C ₁ 、C ₂ }ごとに、攻撃者はU ₁ = Sbox（C 1⊕サブキー[0]）およびU ₂ = Sbox（C 2⊕サブキー[0]）。
サブキー[0]が正しく推測された場合、ΔUを計算するとき、U ₁とU _2の 16組ごとに約3が88になります。
このようにサブキーサブキーの最も可能性の高い最初のバイトを選択すると、攻撃者は2番目のバイトに移動し、同様に3回目のラウンドのキー全体を開くことができます。

最後のラウンドのキーが明らかになった後、攻撃者は最後から2番目のラウンドを攻撃し始めることができ、この方法で行動することは最終的にすべてのラウンド暗号キーに関する情報を受け取ります。

FEAL暗号の説明

次に、上記のアクションを実行しようとする暗号化アルゴリズムを検討します。
したがって、FEAL4はブロック暗号であり、ブロックサイズとキー長は64ビットです。
FEAL4アルゴリズムには同等の説明がいくつかありますが、差分暗号化のデモンストレーションに最も便利なものを使用します。

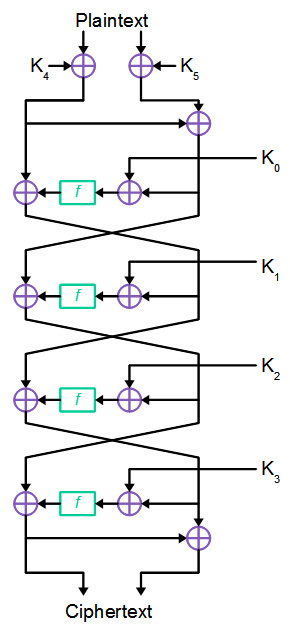
暗号は4ラウンドで構成され、メインキーから生成された6つの32ビットサブキーを使用します（将来、各サブキーは独立して生成されるため、抵抗しきい値を2 ⁶⁴から2 ^192に 「増やす」ことを想定しています）。

初期段階では、平文はそれぞれ32ビットの2つのブロックに分割されます。 左と右のブロックは、それぞれ32ビットのサブキーK [4]とK [5]で2を法として加算されます。 次に、左側の部分は変更されずに残り、左側のブロックにモジュロ2を追加することで右側が形成されます。

その後、4ラウンドの暗号化が実行され、それぞれのラウンドで右ブロックがラウンドK [i]の接続で2を法として合計され、結果が置換関数Fを介して実行されます。置換の結果はテキストの左側に追加されます。 これらの操作の後、左右のブロックが交換され、結果が次のラウンドの入力に送られます。

最終ラウンドは他の皆とは少し異なります。 前のラウンドのように、左右のブロックは場所を変えません。
代わりに、右側のブロックが左側のブロックと2を法として加算され、結果が暗号文の右側として返されます。 4ラウンド後の左側の部分は変更されないままで、受信した暗号文の最初の32ビットを構成します。

作成者によって記述された元の暗号スキームは、上記とわずかに異なりました。 元の説明では、6つの32ビットサブキーの代わりに、12の16ビットサブキーを使用します。 ただし、両方のオプションは同一であり、必要に応じて、32ビットキーを元の説明から16ビットキーとして簡単に表すことができます。



暗号の説明にある唯一の白い点は関数Fです。図では、次のように表すことができます。


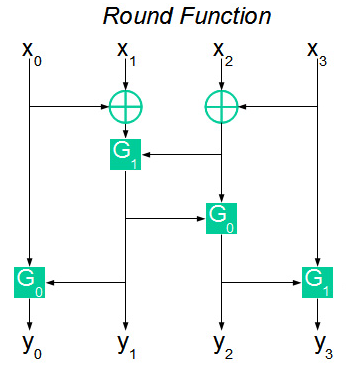
入力で、関数Fは4バイトX ₁ 、X ₂ 、X ₃ 、X ₄を受け取ります。 次に、入力バイトが混合され、関数G ₀またはG ₁を通過します。 関数G _xの計算後に取得された4バイトは、関数Fの32ビット出力シーケンスを形成します。

関数G ₀およびG ₁は、16ビットの入力シーケンスを8ビットの結果に変換します。
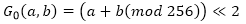
関数G ₀は次のように表現できます。 ここで、<<は左への循環シフトです。
関数G _1の定義は次のとおりです。 。

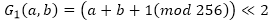
アルゴリズムの復号化も同じ原則に従います。 実際、暗号文は左右のブロックに分割され、すべての暗号化操作は逆の順序で実行されます。
つまり 最初に、最後のラウンドのデコード、次に最後から2番目のラウンドなどが続きます。

FEAL4暗号の差分暗号解読

上記の例のように、置換関数Fを調べることにより、暗号の暗号解析を開始します。これは、FEAL暗号全体の最も重要な欠陥が隠されている場所です。 実際、関数Fは安全性の観点から壊滅的な性質を持っています。 X ₁とX _2の任意の2つの値（X 1⊕X ₂ = 0x80800000の差分）は、Y ₁とY _2に変換されます。 さらに、ケースの100％での差分Y 1⊕Y ₂ = 0x02000000。

これが起こる理由を理解するために、関数Fを計算するときに発生する微分変換を見てみましょう。

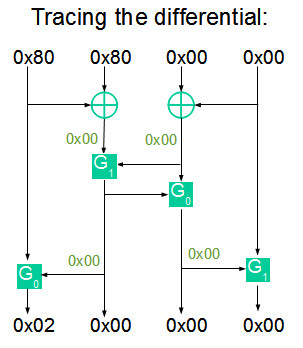
最初のバイトの位置でのみ、ゼロ以外の値が関数Gに入力されることに気付くのは簡単です。 したがって、出力は 。

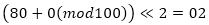
この特性により、暗号が差分暗号解析に対して絶対に脆弱になることは容易に理解できます。 特定の差分ΔYの100％の確率により、攻撃に必要なオープンテキストとクローズテキストのペアの数を最小限に抑えることができます。

最後のラウンドKのキーを解読するために、攻撃者がとるべきステップを検討してください[3]。
攻撃者は、ΔP= 0x8080000080800000になるように、いくつかのプレーンテキストペアP ₁とP _2を生成します。 上記の関数Fの特性を知っている攻撃者は、暗号化のほぼすべてのラウンドで差分を計算できます。

次の図で差分の動作を追跡できます。

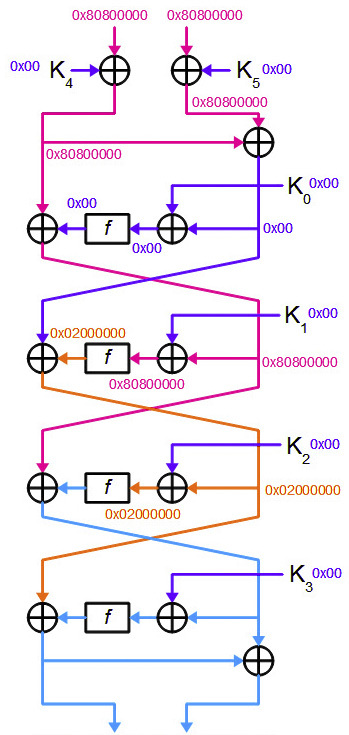
ご覧のように、最終ラウンドまでの差は誤って計算されます。 しかし、これがなくても、攻撃者はすでに最後のラウンドキーを開くのに十分な情報を持っています。
以下の図は、FEAL4暗号の最後の2ラウンドを示しています。

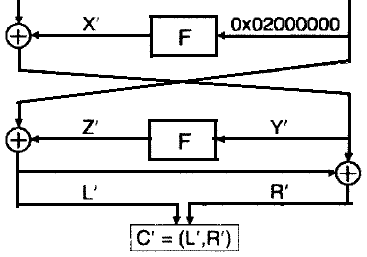
暗号文のペアC ₁とC ₂を持っているため_、攻撃者はΔCを計算し、LとRの値を取得できます。
これに基づいて、彼はZ '= L'⊕02を計算できます。
一方、暗号文C ₁とC _2の各ペアに対して、攻撃者はY ₁とY _2を計算できます。
Y ₁とY _2を知って_、攻撃者はキーKの列挙を開始します[3]。 可能なキーKposごとに、Z ₁ = F（Y 1⊕Kpos）およびZ ₂ = F（Y 2⊕Kpos）が計算されます。 Z 1⊕Z 2のモジュロ2値を追加する_と、攻撃者は結果の値を以前に計算されたZ 'と比較します。 Z '= Z 1⊕Z2の場合、KposはおそらくサブキーK [3]です。
エラーの可能性を減らすために、受信したKposキーを暗号文のいくつかのペアでチェックする必要があります（実装では10ペアを使用しました）。

上記の攻撃には関数Fの2 ^32の計算が必要であることを計算するのは簡単です。これは暗号の作成者が主張する2 ^64ではありませんが、特に4つの丸いキーすべてを計算したい場合、この数字はまだあまり快適ではありませんが、これは間違いなく必要です。
幸いなことに、攻撃は簡単になり、計算の数は非常に快適になります2 ¹⁷ 。
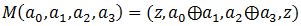
これを行うために、関数の定義を導入します 、ここで、aはバイトのセット、zはゼロバイトです。
各A =（z、a ₀ 、a ₁ 、z）に対して、攻撃者はQ ₀ = F（M（Y ₀ ）⊕A）およびQ ₁ = F（M（Y ₁ ）⊕A）を計算します。
A = M（K [3]）の場合、値Q 0⊕Q ₁の2番目と3番目のバイトが値Z 'の2番目と3番目のバイトと一致することを確認するのは簡単です。 したがって、潜在的なキーKposの2バイトに関する情報を取得します。
その後、b ₀およびb _1のすべての値について、攻撃者はシーケンスKpos =（b ₀ 、b 0⊕a0、b 1⊕a1、b ₁ ）を計算し、上記のように結果のシーケンスをチェックします。

サブキーK [3]を開いた後、攻撃者は3回目のラウンドの後に暗号が置かれた値を復元することができ、これによりサブキーK [2]を同様の方法で攻撃する機会が与えられます。 ただし、ここで、キーK [2]を攻撃するには、異なる初期差分を使用する必要があることに注意してください。 2回目のラウンドでの差分ΔP= 0x8080000080800000は、使用されるキーに対して常に値Z '= 0x02000000になります。 そして、これは2回目のラウンドのキーを推測することはできません。
次の値は、各サブキーを開くための差分として使用できます。
ラウンド4：0x8080000080800000
ラウンド3：0x0000000080800000
ラウンド2：0x0000000002000000
ラウンド1：0x0200000080000000
各ラウンドの4つのキーすべてを開いた後、キーK [5]およびK [4]を計算するのは簡単です。このため、4ラウンドの復号化を通して暗号文を駆動し、結果の値を2を法とする既知の平文を追加するだけで十分です。

攻撃ソースのダウンロードに興味がある場合は、 こちらから入手できます 。

便利なリンク

• 線形および微分暗号解析のチュートリアル
• FEALの差分暗号解析