
少し前のモスクワで、Wolfram ResearchはWolfram
Technology Eraセミナーを開催しました。このセミナーでは、最も強力で間違いなく最も便利なWolfram
Mathematicaコンピューター研究システムの1つについて多くの興味深いことが語られました。 特に、研究グループ「Constructive Cybernetics」によるソーシャルネットワークFacebookのデータの研究結果が発表されました。 少し前に、
Facebookページの包括的な
分析のための新しいWolfram | Alpha機能に出会いました。 そして、結局のところ、頭の中に
「私が住んでいるソーシャルネットワーク(つまり、VKontakte)の友好的なつながりのグラフを見たい」というおかしなアイデアがありました 。 そして、私はまだそれを実装する時間を見つけました。 猫へようこそ。
VK APIとの相互作用は、
https: //vk.com/devでスタンドアロンアプリケーションを作成することから始まり
ます (作成済みのアプリケーションを編集することもできます)。 数回クリックし、名前をよく検討した後、システムは
アプリケーションIDを発行し
ます 。これは、
アクセストークンの取得に使用されます。
Access Tokenを取得するには、以下のリンクをたどって、ラティスを
アプリケーションIDに置き換え
ます 。
ここで 、ラインがどのように形成さ
れるかについて読むことができ
ます 。
https://oauth.vk.com/authorize?client_id=######&scope=friends&redirect_uri=https://oauth.vk.com/blank.html&display=page&v=5.16&response_type=tokenその後、多くの有用な情報、特に
access_tokenと
user_idがアドレスバーに表示され
ます 。 これら2つの値を保存する必要があります。 変数に
myID (整数||文字列)および
トークン (文字列)という名前を付けました。
次のステップは、APIと対話する基本的な関数を作成することです。 VK APIからの標準的な応答形式は
JSONです 。これは、
Mathematicaの内部ツールを使用してリストとルールに簡単に解析されます。

現在使用可能な
メソッドのリストは 、
アクセストークンの形成中に渡された
スコープパラメーターの値によってのみ制限されます。 システムのパフォーマンスを確認するには、名前を調べることができます

VK API出力には多くの不要な要素が含まれているため、有用なデータのみを強調表示するには、まず不要な要素を切り捨てる必要があります

次に、置換ルール(およびこれは置換ルールのリスト)を興味深いパラメーターに適用します。 他のルールは自動的に無視されます。

したがって、ユーザー名と(必要に応じて)彼の写真を受け取るモジュールを書くことができます
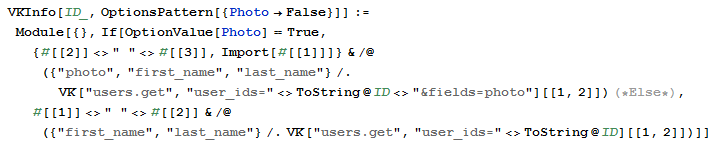
APIのパラメーターは
user_idではなく
user_idsと呼ばれることに注意してください。 これにより、1つのリクエストでユーザーのリスト全体に関する情報を取得できます(IDはコンマで区切り、1000未満にする必要があります)。
ここで、何かを学ぶことに興味のあるユーザーを見つける必要があります。 友達のリストを取得します。 一般に、機能全体は次のとおりです。
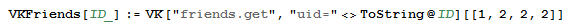
しかし、理想主義への私の欲求と、
Mathematicaの組み込み関数に少しでも思慮深さを近づけたいという欲求のために、
VKFriendsはこの点で私と
一緒に成長しました

ただし、グラフの作成に使用されるのは「
Clean 」バージョンです。 ここで興味深いのは、
fieldsパラメーターを削除した場合、APIからの応答はIDのリストになり、それ以上のものではないことです。 また、
フィールドが少なくとも何か、はい、等しい場合、ユーザー名は自動的に応答に含まれます。 したがって、アバターのないバージョンでは、性別が美しい単語であるという理由だけで、値
フィールド=性が適用されます。 実際には、最終バージョンのフロアの置換ルールは実装されていません。 友だちと一緒に探索したいフィールドをいつでも追加して、そこから美しいヒストグラムを作成できますが、コードは何倍も成長し、その構造を変更する必要があります(もちろん、マスキャラクターに努力しない限り)。
APIがデータを収集するために必要な最後の機能は、相互の友です。 彼らの助けを借りて、あなたの友達のサークル内でのみ接続を調査することができ、あなたの友達が知ら
ない人から何メガバイトの不要な情報を受け取ったり処理したりすること
はありません。 構文と機能を
VKFriendsに合わせるには、少し汗をかかなければなり
ませんでした。
friends.getMutualはIDのクリーンなリストのみを返すことができ、これは明確ではありません(誰かが明確にする必要がある場合)

それだけです! これで、このタスクのVK APIとの統合が完了しました(必要以上に多くのことを行いました)。 尾の
角のリストで
雄牛を捕まえる時です。 行こう!

友人のリストを取得し、接続を説明します。 それらはすべてあなただけに関連付けられています。 実行速度-瞬き。

でも、心配しないでください。お茶を飲んで飲む時間さえあります。
Friends.getMutual自体
は特に高速で
はないため、友人ごとに実行する必要があります。 私の333人の友人では、119秒かかりました。 これは、研究全体で最も長い時間を要する手術です。 この機能は機能しますが、やかんを入れてお茶を選ぶことができます。
DeleteCasesは、結果の配列の深さが突然7になったときにデバッグの過程で発生しました。すべての理由は、友人が共通の友人が何らかの理由で利用できないユーザーを持っているためです。 また、エラーメッセージはルールの形式で表示されます。 したがって、すべてのルールを削除すると、配列の深さは通常になり、データ型は整数(文字列として表される)になります。
コードを実行した結果、
friendsOfFriends変数には、Length [myFriends]のサイズの2次元リストが含まれます。 また、
myFriends (友人)の各要素には、この友人と共通の友人のリストがあります。 ここで、
myFriendsの各友人を、
それに対応する
friendsOfFriendsのすべての友人と接続する必要があります。 ふう。 言葉で説明しているように見えましたが、これに添付のマップを使用すると、完全に判読できなくなります。 したがって、手続き型スタイルで少しいたずらします(自分で繰り返してはいけません。これはMathematicaにとって非常に悪いスタイルです。アセンブラはgotoに基づいており、手続き型プログラミングではそれが悪いスタイルになりましたが、
Wolfram言語ではすべてを分析的に解くことができ、明示的なサイクルは悪いスタイルです[純粋に形式的で、これはそれを新世代の言語にします])

次に、このグラフの作成を試みることができますが、何も機能しません。 頂点の次数が1より大きい無向グラフは、まだリリースされていない
Mathematica 10でのみ追加されます。すべての非有向グラフの頂点の次数は2です。 簡単に言えば、ユーザーAと共通の友人Bを見つけ、ページBを見ると、ユーザーAも共通の友人になりました。 そして、ネットワーク全体を探索した後、すべてのユーザーが2つのエッジで接続し始めました。 これを確認するには、すべての出現に対して
UndirectedEdgeを
DirectedEdgeに置き換えます。 ただし、有向グラフは正確に2倍の冗長性があるため、繰り返されるエッジを取り除き、無向グラフを作成する必要があります。

検証機能がないため、独自の検証関数を作成する必要がありました。 そして、1つには、グラフを一緒に接続します。 奇妙なことに、それはかなり長い間機能します...結果として、
gMyFriendsからのリンクは複製さ
れないため、リンクの数は半分より少し少なくする必要があります。
まあ、すべてを構築することができます! 理解できないものは何もありません。 そのため、明確になるまでコーディングを続けます。
明確にするために、グラフの頂点の外観を変更する必要があります。 これは、
グラフ関数の
VertexShapeオプションを使用して
実行できます。
VertexShapeは、名前を任意のオブジェクトに置き換えるための規則のリストを受け入れます。 この場合の頂点名は
gMyFriendsのリストで
あり 、1つの要素(ユーザー
myID)だけが展開されています。 したがって、
Append [myFriends、myID]リストのすべての要素の情報を取得して、このルールを作成する必要があります。 ゆでたやかんを覚えていますか? それは時間についてです。 お茶を飲むのに数分かかります。

すばらしいのは、すべての情報が1つの要求ですぐに要求されることです。
ToString@Append[myFriends, myID]からブラケットとスペースを削除するだけです。
これで、置き換えが必要なものの配列と、置き換えが必要なものの配列ができました。 しかし、いや、まだその時点ではありません。 すべてが美しい必要があります。

最初に、名前とアバターを持つ長方形のフレームが作成され、対応するIDの隣の3レベルのリストに配置されます。次に、リストのリストの各要素で、関数ヘッダーがリストからルールに変更されます。 その結果、リストのリストからルールのリストを取得します。 (
Wolfram言語は完璧ではありませんか?)
これですべてが確実になりました!

結果を楽しむことができます。 個人的には、この美しさをPDFにしかエクスポートできませんでしたが、キリル文字は表示されないため、ページにロシア語がある場合は、VK関数に「
&v=5.16 」の後に「
&v=5.16 &lang=en 」を追加します。 私の結果はこんな感じ
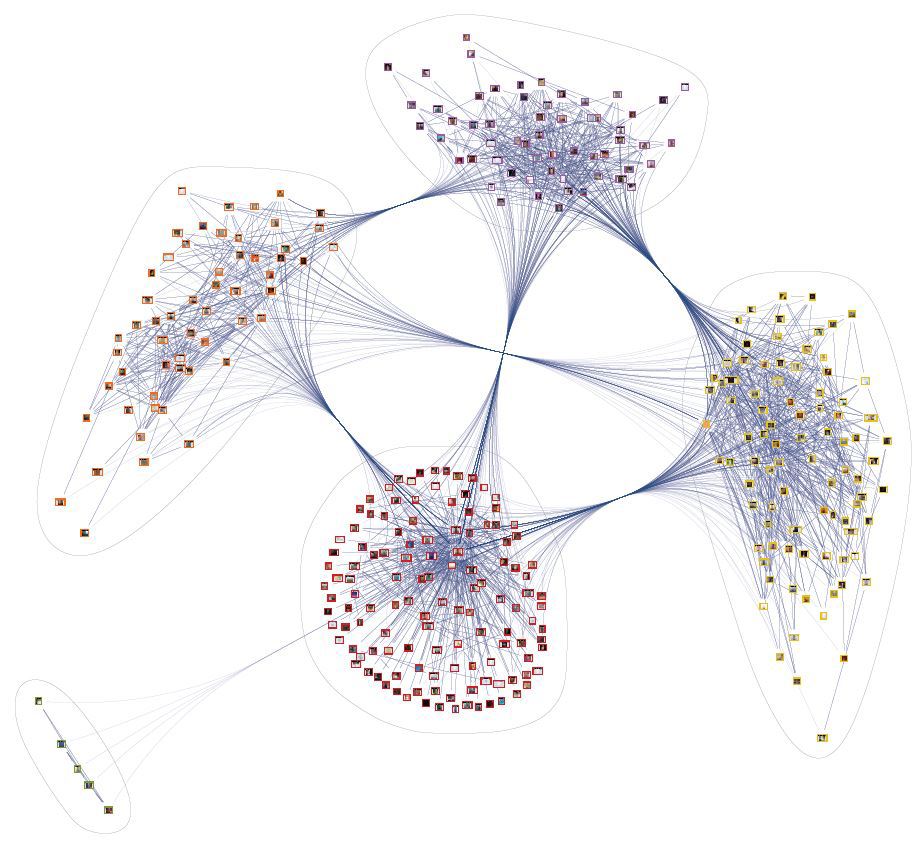

印象的 グローバルに。 特に連絡がコミュニケーションの主な手段である場合。
メモ帳のダウンロードはこちら 。 1回のリクエストで300人を超える人は合格しません。これをさらに共有する必要があります。
(一週間が過ぎました)
今日、彼らは私に、グラフに自分を描くのは役に立たないことを証明しました。 したがって、この接続は冗長です。 グラフを再構築しましたが、変更されました。 また、友達リストを自動的にパーツに分割して結果を収集するメカニズムを追加しました。 実行の進行状況も表示されるようになりました。各リクエストの後に行を印刷し、友人の分割リストにある部分と同じ数の印刷行がある場合、これは100%です。

1回のリクエストで200人を超える人がいる場合、問題が発生することが実験的に決定されました。 最適な量は100です。一般に、小さいほど信頼性が高くなります。 全部で300人の友人がいるので、私は50人います。
それでも、私は共有しなかったすべての人を友人から捨てなければなりませんでした。 これらは慎重に表示され、以降の計算から除外されます。
これはすべて
ここから入手でき
ます。