Habréには、著者がコーナーの3分割を作成し
た記事がありました。 この投稿では、代数場の理論を簡単に紹介する途中で、コンパスと定規によって任意の平坦な角度を正確に3つの等しい部分に分割することが不可能な理由を説明し、これが他のよく知られている建設問題にどのように適用できるかを示します。
はじめに
一対のコンパスと分割のない定規による任意の角度の三等分という有名な仕事は、数千年にわたって多くの数学者を魅了した最も古い問題の一つです。 問題の解決不能、すなわち このような構造の不可能性は19世紀にようやく証明されましたが、一部の人々はまだ解決策を提供しています。 たとえば、ロシア科学アカデミーのある学者の決定が、Science and Life誌に
掲載されました。 おそらく、これはとても繊細なトローリングです...

Science and Life、No。3、1998
確かに、数学のある教授によると、フェルマーの偉大な定理の角度の三分法と
簡単な証明に対する解決策を含む文字の流れは最近著しく減少しました。 現在、彼らは彼に、原則として
、リーマン仮説の証拠を送って
いる 。
フィールド
実際、フィールドは要素の集合であり、それらの間で加算、減算、乗算、除算(ゼロ除算を除く)が可能であり、そのような演算の結果は常に一意に決定され、このフィールドの要素でもあります。 また、実数を使用した算術演算については、フィールドで結果を変更せずに用語/因子を交換し、括弧を開くことができます。
実数Rのセットは、フィールドの最も単純な例です。 そのような数値を使用した算術演算(ゼロ除算を除く)の場合、結果は実数になります。 同様の例は、複素数Cのフィールドです。
有理数Qのフィールドは、整数m、nの分数m / nのセットです。 分数を加算/乗算/除算すると、分数が得られるため、Qがフィールドであることが簡単にわかります。
整数のセットZは、逆に、除算が常に整数を与えるわけではないため、フィールドではありません。5/ 7は整数ではないため、Zには含まれません。
個別に、最終フィールド、または有限数の要素を持つフィールドであるガロア体フィールドに注意する必要があります。 素数pの場合、フィールドF
pはp数のセット{0,1、...、p-1}として表すことができ、pを法として算術演算が実行されます。 たとえば、フィールドF
5では、2 + 3 = 5 mod 5 = 0です。 2 * 3 = 6 mod 5 = 1、したがって1/3 =(2 * 3)/ 3 = 2など 有限体は、代数的誤り訂正符号および暗号化でよく使用されます。リードソロモン符号、AES、および楕円暗号化は、有限体で動作します。
フィールド拡張
フィールドLはフィールドKの拡張であり、Lが完全にKを含む場合、LとKで示され、LとKの演算は同じように動作します。 たとえば、フィールドRは有理数QのフィールドのR / Qの拡張であり、複素数CのフィールドはフィールドRのC / Rの拡張です。
任意のフィールドKと、Kからの係数を持つ変数xのすべての多項式のセットK [x]を考えます。K[x]からの多項式p(x)は、K [x]から(非定数)因子に分解できない場合、フィールドK上の
既約と呼ばれます。 たとえば、多項式P(x)= x
2 +1はRで既約ですが、Cで既約です。 C [x]から因数分解します:x
2 + 1 =(xi)(x + i)。
Kに要素w(Lに含まれるがKには含まれない)とwとKからの要素を含むすべての可能な式をKに追加することで構築できるフィールドKの拡張L / Kに興味があります。次に、フィールドの拡張を次のように示します: L / K = K(w)。 要素wがK [x]からの次数dの既約多項式p(x)の根(つまり、p(w)= 0)である場合、L / K = K(w)= K [x] /( p(x))そして、
Lは次数[L:K] = dの拡張であり、
wは体K上で次数dを持つと言い
ます。 この場合、拡張L / Kは、多項式p(x)を法とするKからの係数を持つ多項式のセットとして表すことができます。 d以下の次数の多項式のセット 1次の拡張L / Kは、初期フィールドL = Kに等しい、つまり 実際にフィールドKを展開しないでください。
複素数のフィールドの例に戻ると、虚数単位を追加することにより、RからC = C / Rを取得できます。
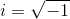
C / R = R(i); さらに、iはR上の既約
2次の多項式x
2 +1(i
2 + 1 = 0から)の根であるため、C = C / R = R [x] /(x
2 +1)は2次の拡張であり、表現可能です。 Rからの係数を持つ最初と0度の多項式のセットの形式で、演算はx
2 +1を法として実行されます。 または、同等に、

。
うわ 難しい理論は終わり、それから簡単で楽しい練習が始まります。
コンパスと定規
今、私たちは何が可能か、コンパスと定規の助けを借りて何を構築できないのかを自問しますか?
このような構造は、ユニットセグメントを定義する平面上の2つのポイントから始まります。 これらのポイントが
構築されたと考えます。 2つのポイントを作成したら、それらを通る直線を描くか、1つのコンパスを使用して、一方を中心にもう一方を通る円を作成します。 これらの線と円は、構築済みとも呼ばれます。 構築された線と円の交差点は、新しい線や円などを描くことができる新しい構築点を提供します。 これにより、コンパスと分割のない定規を使用した操作が使い果たされます。 有限数の同様の操作でポイントとラインを構築できる場合、それらに
到達できます。
デカルト座標系0xyを導入します。このシステムでは、最初の2つの点の座標は(0,0)と(1,0)です。 数字a、b、c、d、a '、b'、c '、d'がフィールドKに属していると仮定します。このような座標を持つ点で構成された線は、フィールドLの座標と交わることが示されます。 [L:K]≤2。
示す必要がある点(a、b)、(c、d)を通る直線は、式(ac)(yb)=(bd)(xa)で与えられます。 中心(a、b)が(c、d)を通る円の方程式は、(xa)
2 +(yb)
2 =(ca)
2 +(db)
2で与えられます。 2組の点(a、b)、(c、d)および(a '、b')、(c '、d')から構成される直線および円の方程式の係数もKにあります。このような2つの直線の交点の座標は次のとおりです。線形システムを解くことにより
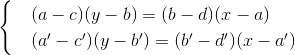
解は、方程式の係数の線形関数の関係によって表されます。つまり、(x、y)もKに属します。線と円の交点の座標は、システムから取得されます。
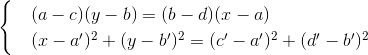
最初の式からxからyまでを表現し、2番目の式でxを代入して除外すると、Kから係数を持つyの2次方程式が得られます。解は係数とルートの線形結合で表されます。
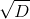
方程式の判別式Dから。 ルートは必ずしもKの要素ではなく、拡張要素です
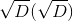
。 DがKの完全な正方形でない場合、2次の拡張があります。
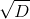
既約多項式の根

。 xの同様の引数
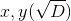
。 判別式が負の場合、解は虚数であり、円は線と交差せず、新しい点は形成されません。
最後に、2つの円の交差点
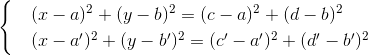
一方の方程式から他方を引き、x
2 、y
2を減らし、x、yで線形の方程式を取得します。 システムに新しい方程式を追加すると、直線と円の交点の場合になります。
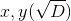
。
(a、b)=(0,0)、(c、d)=(1,0)、(a '、b')=(-4 / 9,3)、(c '、 d ')=(1 / 3,1 / 2)Qからの座標。2つの線の交点、円と直線、これら4つの点に構築された2つの円の座標は座標を持ちます。
(x
0 、y
0 )=(22 / 45.0)、
(x
1 、y
1 )=
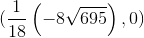
、
(x
2 、y
2 )=
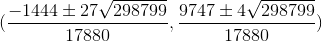
、
それに応じて。 x
0 、y 0∈Q、線は円と交差しない、x
2 、y
2 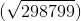
。
したがって、図面に新しい線を追加すると、新しく作成された点の座標は現在のフィールドKまたはその次数2の拡張L / Kにあります。L/ Kからの点に新しい円を作成すると、L / Kフィールドの拡張が形成されます:E / L、[E:L] = 2。 連続する拡張の次数が乗算されます。つまり、Eは次数のフィールドKのE / Kの拡張です[E:K] = [E:L] [L:K] = 2 * 2 = 2
2 。 したがって、
到達可能なすべてのポイントは、フィールドKの拡張からの座標が2 n度のみです。 ポイント(a、b)の構築は、ポイント(a、0)、(b、0)の構築と同等なので、以下では単に「長さaのセグメントを構築する」または「数bを構築する」と言います。
三等分角

点(0,0)で角度ξで交差する線のペアを与えます。 他の開始点(1,0)と組み合わせて、角度を定義することは、長さcosξのセグメントを定義することと同等です。つまり、フィールドQ(cosξ)の数値から構築を開始します。 同様に、角度ξ/ 3の構築は、長さcos(ξ/ 3)のセグメントの構築と同等です。 三角関数の同一性cosξ= 4cos
3 (ξ/ 3)-3cos(ξ/ 3)は、
座標pから始まる多項式p(x)= 4x 3 -3x-cosξの根(長さcのセグメント)を構築する必要
があることを示して
いますフィールドQ(cosξ) ただし、ほぼすべての角度ξについて、この多項式は体Q(cosξ)で既約です。 たとえば、ξ= 60°cosξ= 1/2の場合、多項式p(x)= 4x
3 -3x-1 / 2は体Q(cosξ)= Q(1/2)= Qを因数分解しません。 cos(ξ/ 3)はフィールドQ(cosξ)の拡張Q(cos(ξ/ 3))= Q [x] /(p(x))にあり、既約p(x)の場合のこの拡張は次数多項式p(x)の3≠2
nである場合、cos(ξ/ 3)はセグメントの到達可能な長さまたはポイントの座標ではありません。 したがって、これらの場合、角度の正確な三等分は不可能です。
もちろん、三等分できる角度があります。 たとえば、ξ= 90°の角度を持つ(さらには持たない)30°の角度を作成するのは簡単です。 この場合、多項式p(x)= 4x
3 -3x-cosξ= 4x
3 -3x = x(4x
2 -3)はQ(cosξ)= Qで因数分解されます。 cos 30°の既約多項式は4x
2 -3、拡張Q(cos(ξ/ 3))= Q(
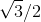
)Qに対して次数2を持ち、その要素はコンパスと定規で簡単にアクセスできます。 しかし、このような良い角度は無視できます。
おわりに
同様のアプローチは、コンパスと定規を使用した他の幾何学的構造の可能性の証明にも使用されます。
- キューブを2倍にする作業-もう1つの解決できない古代の問題-は、1組のコンパスと定規を使用してキューブの端を構築することです。 長さセグメントの構築
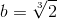 特定の単一セグメントに対して。 bはQ上の既約多項式x 3 -2の根であり、Q上の次数3≠2 nであり、したがって達成不可能であることは容易にわかります。
特定の単一セグメントに対して。 bはQ上の既約多項式x 3 -2の根であり、Q上の次数3≠2 nであり、したがって達成不可能であることは容易にわかります。
- 同様の状況は、円の求積法でも得られます。これは、与えられた円と同じ面積の正方形を作成するタスクです。 タスクは、数値を構築することです
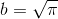 、これは一般にQ [x]の多項式の根ではなく、Qを超える次数を持ちません。
、これは一般にQ [x]の多項式の根ではなく、Qを超える次数を持ちません。
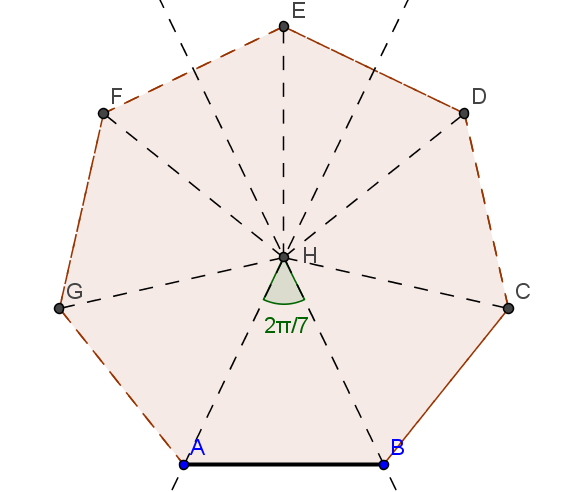
- 通常の七角形の構築は不可能です。 これは、フィールドQから数cos(2𝜋 / 7)および\またはsin(2𝜋 / 7)を構築することになります。ユニティz = e 2𝜋 / 7の7次根は根x 7 -1 =(x-1)(x 6 + x 5 + ... + 1)およびQに対して次数6 2番目の要因は既約です。 一方、z = cos(2𝜋 / 7)+ i sin(2𝜋 / 7)∈L(i)であるため、zはL = Q(cos(2𝜋 / 7)、sin(2𝜋 / 7))に対して次数2を持ちます。 [L(i):L] = 2。 したがって、LはQ に対して次数6/2 = 3≠2 nであり、到達できません。
- 逆に、z = e 2𝜋 / 17はルートx 17 -1 =(x-1)(x 16 + x 15 + ... + 1)であり、次数16 = 2 4であるため、通常の17角形を構築できます。一般に、これは任意のpゴンに対して機能します。ここで、pはp-1 = 2 nのような素数です。 そのような数はフェルマー素数と呼ばれます。 ピエール・フェルマー自身は、2 2 ^ n +1の形式のすべての数字は単純で、習慣に忠実で、証明されていないと主張しました。 しかし、これはすぐに反論されました。 フェルマーの最大の既知の素数に対応するレギュラー65537ゴンは、1894年に通常のコンパスと定規を使用して、忍耐力に優れたヨハンエルメスによって建設されました。
豊富な計算で親愛なる読者を飽きさせず、このような簡単な例を使用して数学のさまざまなセクションの美しさと密接な相互関係を実証できたと思います。 私はコメントやコメントを見てうれしいです。