すべての人に良い一日を! この短い投稿は、ウォーターフォールとアジャイルの開発プロセスのモデルの検討に専念しています(スクラムおよび/またはかんばんの例)。 そして、ここにあります:顧客の観点から、プロセスは機能の面で満足のいく結果の時間と予算ほど重要ではありません。 そして、(変更が考慮されていない)ことがわかっている場合、ウォーターフォールプロセスのコストはS曲線に沿って進み、アジャイルプロセスのコストは線形に累積します(すべてのリソースが同時に使用されるため)、効率がどのように異なるべきか。 この問題を調査するには、モデルを作成して比較する必要があり、このために単純な数学が使用されます。
ヒント#30:可能な限り検討してください。 カウントできない場合は、計算してください。 最後の手段として、専門家の判断に基づいた推定値のみを使用してください。
McConnell S.ソフトウェアプロジェクトコストはいくらですか(2007)。
|
背景
プロジェクト管理は、条件付きで、計画と管理という2つのコンポーネントに分けることができます。
この観点から、ウォーターフォールのすべてが明確です。期限の割り当て、割り当てられたタスク、および先に実装されたタスクに従って、タスクの段階的な(分析-開発-テスト)スケジュールをまとめました。
スクラムとかんばんはそれほど複雑ではありません:計画シーケンスはバックログの優先順位によって実行され、開発はプロジェクト全体のバーンダウンチャート(スクラム)またはリードタイム(かんばん)を使用して制御されます。 タスクの複雑さの評価には、用語の推定が伴います。3回の反復またはタスクにより、終了日を推定できる速度に基づいて速度が明らかになります。
この投稿では、プロジェクトの進捗はモデル化されません(これは完全に独立したタスクです)が、計画された効率は比較されます。
「ペンの先端で」
計画を2つのコンポーネントとして提示します。
- プロジェクト製品全体のタスクの複雑さのユニット(ストーリーポイントのアナログ)の総数( P )、
- 時間tに関係する人員の数は、 n(t)<= N (アジャイルの場合の平等)です。
次に、1人の専門家がタスクの1単位の複雑さを実行
する時間を
cで示し、
cは単位時間あたりの1人の専門家のコスト、
Tは総プロジェクト時間、
Sはその予算、
p = p(t)は時間
tで実行される作業量。
次に、アジャイルについては、
N人が一度にタスクユニットを実行するのと同じくらいの時間をかけて、単位時間内に作業を行うことができます。
p ' A (t)= N / r =>(最初に作業が行われていないことを知っている)
p A (t)= N * t / r実際には、以下から明らかです。
T A = r * P / N; S A (t)= c * N * t; S A = c * r * P.それは実際にはすべてとても明確です明らかに、合計でどれだけの人が仕事をするか、時間とコストを掛け、プロジェクトにどれくらいのコストがかかるか。 同時に、1つの問題を解決するのにかかるコストとタスクの数を掛けたコストがかかります。
これがアジャイルの完成です。幸いなことに、彼の計画のモデルは(私のバージョンでは)非常にシンプルでした。 プロジェクト中に専門家が関与しているため、ウォーターフォール計画ではすべてが複雑になります。 ただし、この場合、主な関係は残ります。
p '(t)= n(t)/ r関数
n(t)を選択することがすべてです。 ゼロではゼロであり、プロジェクトの終了時にはゼロであることを知っています。 他に何も知りません さらに、対称で、中央で
Nに達し、二次関数的に成長すると仮定します(これは、与えられた条件下で最も単純なオプションであるという考慮事項から二次関数を選択しました)。
n(t)= N * 4 *(T-t)* t / T 2 。
p(0)= 0であることがわかっているので、積分
p '(t)を書き出すことができます。
p(t)= 2 * N * t ^ 2 /(r * T)-4 * N * t ^ 3 /(3 * r * T ^ 2) =>
T = 3 * P * r /(2 * N )ああ! しかし、これはすでに興味深いです! プロジェクトを時間内にプロジェクトに引き付けるという選択された法則により、プロジェクトの長さは1.5倍になります! しかし、すべての人員が関与している状況は、Waterfallの典型的な例です。それはすべて再び直感的です人々がすぐにタスクを実行すると、時間が短縮されることは明らかです。 同時に、常に最大N人が関与している場合、これはプロジェクト時間の最小の状況です。
費用はどうですか? 統合によっても見つけることができます(
t内 )。
s '(t)= c * n(t) =>
s(t)= 2 * c * N * t ^ 2 *(3 * T-2 * t)/(3 * T ^ 2) 、
どこから
S W = 2 * c * N * T / 3 = c * P * r 。
予算は同じです。
不思議ではないそして、仕事の量が同じなら、なぜ彼は違うのでしょうか?
曲線
区間
[0;で Sカーブを取得したことを確認し
ます。 T] 。 値
c = 1、r = 2、P = 100、N = 10を代入し、
T = 30を取得します。
ウォーターフォールのグラフ
p = p(t) :

ウォーターフォール
のグラフ
s = s(t) :
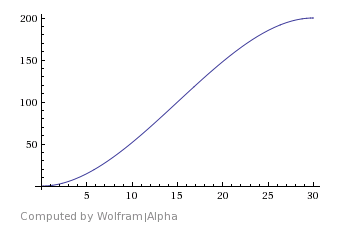
Sカーブ計画は一度に実行される作業量を決定するため、これは
ロジスティックカーブではありません。人数は、どの時点でどれだけの作業を行うかに依存しません。
いくつかの結論
誰かがこのポストキャプテンを考慮し、真実から遠くないでしょう。 結局のところ、モデルはやや "共食い"であり、変更(本質的には計画の更新)を考慮していません。 同時に、WaterfallとAgileで異なる人数を収集する場合、日付は同じにすることができますが、予算は異なります。
アジャイルが最適であるとは言いません(そのようなシミュレーションでは時間の面で極値であるという事実にもかかわらず)-モデルには単純化が多すぎます。 しかし、考慮されたメカニックが異なるアプローチの効果の違いを説明し、誰かが設計計画を最適化するために考慮された原則を採用する可能性は十分にあります:問題をすぐに解決するためにできるだけ多くの人を引き付けることは、予算を維持しながら時間を短縮できます予算が増えると思われるかもしれません)。