記事の続きで
最初の
記事では、最初のプリミティブをすでに使用していましたが、これは単に「任意の形式」と呼ぶことができます。
プリミティブオブジェクトを説明する前に、システムの2つの主要な要件であるコメントをもう一度繰り返します。
- 各プリミティブには、頂点ベクトルとインデックスベクトル(頂点、インデックス)が含まれている必要があります。
- 各プリミティブは、三角形(TRIANGLE)を介したインデックスで構成されます。つまり、3点ごとに独立した三角形が形成されます。
各プリミティブの要件に加えて、
マトリックスを接続できます。 接続後、次の操作を簡単に実行できます。
- 軸のいずれかに沿って移動します。 特定のユニット数に移動するか、空間内の任意のポイントに移動します
- 任意の点を中心に回転します。 マトリックスが接続されると、中心がそれぞれ認識されるようになり、ポイントを示す任意のポイントまたはその中心を中心にプリミティブを回転させることができます。
プリミティブ自体は分割できます。
- シンプル。 それらは1つのプリミティブのみで構成されます。
- 複雑です。 いくつかのプリミティブで構成されます
単純なプリミティブ
平野
説明
このプリミティブは平らな長方形です。 構築するには2つの三角形で十分です。 取得する必要がある入力データの最小値は、フィギュアの中心、その幅と高さです。 出力では、少なくとも2つの配列(頂点の配列、インデックスの配列)を取得する必要があります。 各頂点を中心、幅、および高さから計算するため、左上の頂点はxが中心から幅の半分まで左にオフセットされ、yが高さの半分まで上にあり、zはシフトしません。図はフラットです。 同様に、他のすべての頂点を見つけます。
[this.frontCenter[0] - width / 2, this.frontCenter[1] + height / 2, this.frontCenter[2], this.frontCenter[0] + width / 2, this.frontCenter[1] + height / 2, this.frontCenter[2], this.frontCenter[0] + width / 2, this.frontCenter[1] - height / 2, this.frontCenter[2], this.frontCenter[0] - width / 2, this.frontCenter[1] - height / 2, this.frontCenter[2]];
インデックスの配列で、ポイントの結合方法を決定します。 このプリミティブには2つの三角形があります
左上の点、右上の点、左下の点。 頂点の配列では、これらは要素です-0,1,3
右上点、右下点、左下点。 頂点の配列では、これらは要素です-1,2,3
したがって、インデックスの配列は次のとおりです。
[0,1,3,1,2,3、];
インデックスの順序は変更されませんが、頂点にいくつかの変更がある場合があります。 プリミティブで簡単に操作できるように、頂点の配列を行列に変換します。
this.matrix = new botuMatrix(this.vertex,3);
プリミティブ操作
マトリックスを操作すると、入力パラメーターとして渡された配列、この場合は頂点の配列が変更されます。
マトリックスを説明するときに、
マトリックスで可能な操作が示されました。 操作データをプリミティブに接続します。
moveByX:function(value){ this.matrix.move(value,0); }, moveByY:function(value){ this.matrix.move(value,1); }, moveByZ:function(value){ this.matrix.move(value,2); }, testToPoint:function(value){ this.matrix.toPoint(value); }, rotateAroundCenter:function(angle,xyzType) { this.matrix.rotate(angle,this.matrix.center,xyzType); }, rotateAroundMaxPoint:function(angle,xyzType) { this.matrix.rotate(angle,this.matrix.maxval,xyzType); }, rotateAroundPoint:function(angle,point,xyzType) { this.matrix.rotate(angle,point,xyzType); },
- moveByX、moveByY、moveByZ-プリミティブをそれぞれX、Y、Zに移動します。 唯一の入力パラメーターはユニット数です。 例、obj.moveByX(50)-objを50ユニット右に移動します。
- testToPoint-プリミティブ(セントにフォーカス)を特定のポイントに移動します。 入力パラメーターは点ベクトルです。 例obj.testToPoint([0.50.10]);
- rotateAroundCenter、rotateAroundMaxPoint-中心または最大座標を中心に回転します。 (長方形の例では、最大座標は右上の点と一致しますが、最大座標はプリミティブのどの点とも常に一致するとは限りません。ほぼすべての3次元オブジェクトが立方体にパックされる場合、最大座標はこの立方体の一番上の点になります。) 入力パラメーターは、ピボットの角度とピボットの軸です。 例:obj.rotateAroundCenter(45、 "byX")-X軸を中心とした45度の回転。 角度は度、軸-「byX」、「byY」、「byZ」で示されます。
- rotateAroundPoint-空間内の任意の点を中心にピボットします。 例、obj.rotateAroundPoint(45、[0,0,0]、 "byZ");
これらの操作はプリミティブに依存しないため、今後はコメントなしで接続します。
カブ
このプリミティブは六面体です。 ほぼ立方体で、面のみが正方形または長方形のいずれかです。
説明は長方形の説明と同じになりますが、別の入力パラメーター-depthのみを追加します。
立方体は、遠くと近くの長方形のように8つの頂点を持ちます。 上記の単純な長方形との違いは、Z座標の計算にあり、近くの長方形では深さの半分だけ減少し、遠くの長方形では深さの半分だけ増加します。
これを行うには、2つのセンターを取るだけです
this.frontCenter=[centerPoint[0],centerPoint[1],centerPoint[2] - depth / 2]; this.backCenter=[centerPoint[0],centerPoint[1],centerPoint[2] + depth / 2];
そして、配列に2つの長方形を作成します。最初の長方形は中央のfrontCenterで、2番目の長方形は中央のbackCenterです。
this.frontCenter[0] - width / 2, this.frontCenter[1] + height / 2, this.frontCenter[2], this.frontCenter[0] + width / 2, this.frontCenter[1] + height / 2, this.frontCenter[2], this.frontCenter[0] + width / 2, this.frontCenter[1] - height / 2, this.frontCenter[2], this.frontCenter[0] - width / 2, this.frontCenter[1] - height / 2, this.frontCenter[2], this.backCenter[0] - width / 2, this.backCenter[1] + height / 2, this.backCenter[2], this.backCenter[0] + width / 2, this.backCenter[1] + height / 2, this.backCenter[2], this.backCenter[0] + width / 2, this.backCenter[1] - height / 2, this.backCenter[2], this.backCenter[0] - width / 2, this.backCenter[1] - height / 2, this.backCenter[2]
インデックスのトップについて。 立方体には6つの面があり、それぞれ2つの三角形で構成されています。
/ *私たちに最も近い長方形、キューブを操作する前に表示される唯一の長方形* /
0、1、3
1,2,3
/ *左側* /
0.4.7
0.3.7
/ *結論* /
3,7,6
6.3.2
/ *右側* /
2.6.1
1,5,6
/ *上面* /
0.4.5
0,5,1
/ *裏面* /
7.4.5
7,5,6
複雑な複合プリミティブ
単純なプリミティブ。 作成した三角形は三角形で構成されており、このプリミティブを作成する前に、精神的に三角形に分割しました。 複雑なプリミティブは、他の幾何学的な2次元図形で構成されます。 この記事では、唯一の「複雑なプリミティブ」、つまりボールについて検討します。 これは長方形で構成されます。
ボール
ボールを描くために知っておくべきこと-座標と半径? はい しかし、もう1つの小さなパラメーター-詳細を追加します。
これは同じ円で、同じ半径で、詳細が異なるだけです。 プリミティブの説明で詳細として理解されるという事実-少し後で。

詳細設計-35
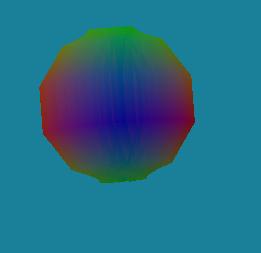
詳細設計-10
アルゴリズム:
- 接線に沿って長方形を作成します。つまり、長方形の中心は、Z軸に沿って半径だけ変位した円の中心です。 長方形の高さと幅は円の長さで、半径を詳細で割って計算されます。 細部が詳細であるほど、長方形の高さと幅が小さくなるほど、長方形自体が多くなります。
- 360 * /(前のステップで見つかった長方形の数)に等しい角度で回転させて、上部にもう1つの長方形を追加します。
- 前のステップをn回繰り返します。 ここで、nは長方形の数です。 その結果、車輪が手に入ります。

- 360 * /(円の長さを幅で割った値)に等しい角度だけY軸に沿って回転するこのホイールのコピーを作成します。
- 前の操作をn回繰り返します。nは、円の長さを幅で割った値です。
このアルゴリズムを実装するには
- 他のオブジェクトを接続できるオブジェクトを作成します。 コードの観点から、頂点の配列と異なるオブジェクトのインデックスは、頂点とインデックスの配列に追加されます。
function botuGroupedObject(){ this.vertex = []; this.indices = []; } botuGroupedObject.prototype = { addObject:function(obj){ this.vertex.size = obj.vertex.size; var next = Math.max(this.vertex.length / this.vertex.size,0); this.vertex = this.vertex.concat(obj.vertex); this.indices = this.indices.concat(obj.indices.map(function(i){return i + next})); this.vertex.size = obj.vertex.size; } }
- 新しいオブジェクトにオブジェクトのコピーを作成するための補助関数を作成します。
function makeCopy(object,type){ var vertex = object.vertex.slice(0); var indices = object.indices.slice(0); return new type(vertex,indices); }
- プレーンプリミティブにメソッドを追加する
connectUP:function(anotherPlain){ var downLeftPoint = anotherPlain.getDownLeft(); var dvPoint = downLeftPoint.map(function(value,index){return value - this.getUpperLeft()[index]},this); this.testToPoint(dvPoint); }
プリミティブ-プレーンは、別のプリミティブプレーンの上部境界の近くに構築されます。 getDownLeft()は、左下のポイント、つまりインデックス3の頂点の配列の要素です(上記のプレーンプリミティブの説明を参照)。 getUpperLeft()は左上のポイント、つまりインデックス0の頂点の配列の要素です。
仕事の一例。