10の面白いタスク

列車の進入速度は時速100 kmで、それらの間の距離は100 kmです。つまり、1時間で会います。 フライは、この時間中に200 km / hの速度で飛行し、合計200 kmを飛行します。

MBCの三角形では、CMの脚はBMの斜辺よりも小さくなっています。 MC = AM。 したがって、MB> AM。 辺MBが辺AMよりも大きい三角形ABMを考えてみましょう。 それどころか、大きい側が大きい角度です。 したがって、∠CAB>∠ABM。 Chtd。

タスクはトラップです。 「家族の中で正確に1人の少年」という規則は、国内の少年全体の可能性に影響を与えません。 正解は50％です。

タスク全体が28のタスクで構成されていると仮定します。 最初のものはリゾルバでタスクの半分（14の問題）を14/7 = 2時間で解決し、2番目はこの時間中に2 * 4 = 8の問題を解決します。 リゾルバーで武装し、2番目は20/7 <3時間で残りの28-8 = 20の問題を解決し、この時間の最初は3 * 4 = 12の問題のみを解決し、すべてで14の問題があります。 したがって、2番目の女の子は、タスクに早く対処します。

アルキメデスの法則を思い出してください。浮力は、液体に浸された体に作用し、この体によって置換された液体の重力に等しい。 ボディは液体で完全に囲まれているか、液体の表面と交差している必要があることに注意してください。 したがって、たとえば、アルキメデスの法則は、プールの底にあるスクラップには適用できません。 したがって、氷とスクラップが浮いている間、スクラップと氷の質量は移動した水の質量に等しくなります。 スクラップが底に沈むと、それによって置換される水の量はスクラップの量に等しくなります。 氷の質量は、融解時に変化した水の質量に等しいため、氷の寄与は無視できます。 （ちなみに、同じ理由で、スクラップが元の問題に含まれていなかった場合、答えは水位が変わらないということです。）溶解する前に、水はスクラップより密度が低いため、混雑は融解後よりも多くの水を押し出しました。 回答： プール内の水位が低下します。 （氷とスクラップが水面ではなく水柱に浮いたと仮定すると、理論的根拠は完全に単純化されます：氷が溶けたときに氷の体積が減少し、スクラップの体積は変化しませんでした。）

ニュートンの箱を思い出してください。

最後の式では、pは素数であり、二項係数の式の分子にあり、分母はpより小さい数の積であるため、各二項係数はpで除算されます。 Chtd。

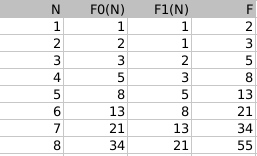
F（N）は、行に2つの単位を含まない長さNの行の数を示します。 F0（N）で表示し、長さがNの行に2単位を含まず、0で終わる行を示します。F1で表示します（N）長さNの行に2単位を含まず、1で終了します。

F0とF1の繰り返し式を導き出します。
F1（N）= F0（N-1）。 2つのユニットを連続して配置することはできないため、1で終わる行の数は、1の短い長さで0で終わる行の数に等しくなります。
F0（N）= F0（N-1）+ F1（N-1）。 条件に違反することなく、正しい行にゼロを追加できます。 したがって、0で終わる行の数は、1つの短い長さの行の数に等しくなります。

F0（N）= F0（N-1）+ F1（N-1）= F0（N-1）+ F0（N-2）。 したがって、F0は特定のシフトを持つフィボナッチ数列です。 F1（N）= F0（N-1）。つまり、F1はフィボナッチ数で構成され、F0に対して「遅れ」は1です。

F（N）= F0（N）+ F1（N）。 F（N）という用語は、フィボナッチ数列F0の数がフィボナッチ数列F1の数に加算されるときに取得されます。これは、その前の数です。 また、フィボナッチ数と前のフィボナッチ数の合計もフィボナッチ数です（フィボナッチ数の式による）。 したがって、 1つの行に2つの単位を含まない行の数がフィボナッチ数になることを証明しました。 最初の2つのNのF（N）の値を決定します。F（1）= 2（2つの適切なシーケンス：「0」と「1」）、F（2）= 3（3つの適切なシーケンス：「00」、「01」 、「10」）。

重要な条件は、最初は単一の株主が彼のサインの後ろに座っていないという事実です。 テーブルの状態の数もNです。テーブルの状態の1つ（初期）では、プレートに座っている株主はいないため、株主とタブレットを比較できるテーブルの条件はN-1です。 これらのN-1状態について説明します。 この間、N人の株主全員がサインに「行く」必要があります。 ディリクレの原理によれば、検索されるN-1個の状態の少なくとも1つはN個の比較のうち少なくとも2つを持たなければなりません。 言い換えれば、少なくとも2人の株主が自分のサインに座っているという条件があります。 Chtd。

白いキャップを1つ、黒いキャップを0で表します。 最後のセージは、 2を法とするスタンディングセージの前のキャップの色を加算します（それらをXorit）。 結果の量に対応する色を指定します。 最後の賢者のさらなる運命はそれほど興味深いものではありません。おそらく、名前のついた色は彼の帽子の色と一致したかもしれません。 次のセージは、立っている人の前の帽子の合計を計算した後、最後のセージと呼ばれる色でそれを合計し、彼が呼ぶ帽子の色を取得します。 次のものは3つの数字を合計します：前に立つ白い帽子の数と2つの前の賢者によって言われた数。 後続のセージも同じように機能します。 少なくともN-1個の正解が判明しています。