この記事は、フラクタルに関する一連のヘアスタイルの最後です。 ハブラスタティア
「ヒルベルト曲線を使用して絵を描く」では、 Gavという子猫について、ハブラスタティアでは
「複雑な平面上のコッシュ」 、フラクタルは地平線に流れ込み、ハブラスタティアでは
「フラクタルの夜」 、暴走時間アルゴリズムについて話しました。 この記事では、霧の中のハリネズミ、そしてもちろん猫について説明します。

少なくともわずかでもフラクタルに出会った人は誰でも、ジュリア集合の美しい絵を見ました。それは正方多項式で定義されています。 しかし、逆問題を解くのは興味深いことです。いくつかの図があり、それに沿って、元の図の近似を与えるような多項式を考え出します。 上記のハリネズミの写真はこの考えを示しています。
だから、猫
Kを検討してください

猫の内部では、シーケンス
f (
z )、
f (
f (
z ))、
f (
f (
f (
z (
z )))、...が有界であるが、猫の外部では無限になる傾向があるような多項式
fを考え出す必要があります。 私は長い間この質問について考えていませんでしたが、すぐにインターネットを検索し、
Kathryn A. Lindseyによる素晴らしい記事、
「Shapes of Polynomial Julia Sets 」 、2013、
arXiv:1209.0143を見つけました 。 この記事は、
「良い」猫と与えられた精度δに対して、そのような多項式が発明され、その証明が建設的であることを証明します。
この設計を検討してください。 φ 'を単位円の外側を猫の外側に変換する等角写像とします。 φ(
z )=φ '((1 +ε)
z )をいくつかの小さなεに対して修正された元のマップとします。
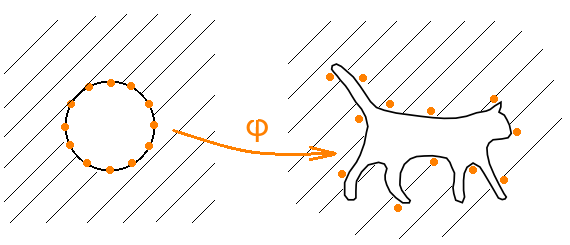
さらに、ω(
z )=
c - n (
z -
r 0 )(
z -
r 1 )⋅...⋅(
z -
r n -1 )、ここで
cはローラン級数のマップφの展開における
zの係数、
r k =φ(
e2πik / n )は、n次の単一性の根のイメージです。 多項式
f (
z )=
z (ω(
z )+ 1)は、十分に大きい
nに対して望ましいものであることが証明されています。
したがって、問題を解決するには、対応する等角写像を生成する方法を学ぶ必要があります。 インターネットでの小さな検索の結果、
ジッパーパッケージが見つかりました。 このパッケージを使用すると、ポリラインで囲まれた領域への単位円の内部の等角写像を見つけることができます。 このパッケージは20年前
に古代の方言で書かれましたが、それを組み立てて使用することは難しくありませんでした。
古代の方言の一部call invers write(4,*)z1,z2,z3,zrot1,zto0,zto1,angler,zrot2 do 981 j=4,n-2,2 981 write(4,999)a(j),b(j),c(j) zm=dcmplx(0.d0,0.d0) ierr=0 do 982 j=1,n if(cdabs(zm-z(j)).lt.1.d-16)then ierr=1 jm=j-1 write' WARNING: prevertices',j,' and',jm,' are equal' endif zm=z(j) x=dreal(z(j)) y=dimag(z(j)) 982 write(3,999)x,y if(ierr.eq.1)then
Pythonの接着剤でジッパーをコーティングする def calc_phi(points): with open("init.dat", "w") as output_file: for point in points: output_file.write(str(point.real) + " " + str(point.imag) + "\n") output_file.write("\n0.0 0.0\n") os.system("echo \"init.dat\n200\npoly.dat\" | ./polygon") os.system("./zipper") os.system("rm init.dat") def transform_points(points): with open("fftpts.dat", "w") as output_file: for point in points: output_file.write(str(point.real) + " " + str(point.imag) + "\n") os.system("echo \"0\nfftpts.dat\nfftpts.img\n0\" | ./forward") transformed_points = [] with open("fftpts.img", "r") as input_file: for line in input_file.readlines(): x, y = float(line[0:25]), float(line[25:]) transformed_points.append(complex(x, y)) os.system("rm fftpts.dat") os.system("rm fftpts.img") return transformed_points
このパッケージを使用するには、イメージ上にポリラインを作成する必要があります。 自動決定は行いませんでしたが、画像をInkscapeエディターにアップロードして丸で囲んだため、SVG形式を簡単に解析できました。 これは、ポリラインを試すことができるため便利です。
SVGファイルのパスの解析 def read_points_from_svg(file_name, path_n): with open(file_name, "r") as input_file: content = input_file.read() soup = BeautifulSoup.BeautifulSoup(content) path = soup.findAll("path")[path_n] data = path.get("d").split(" ") x, y = 0, 0 is_move_to = False is_relative = False points = [] for d in data: if d == "m": is_move_to = True is_relative = True elif d == "M": is_move_to = True is_relative = False elif d == "z": pass elif d == "Z": pass elif d == "l": is_move_to = False is_relative = True elif d == "L": is_move_to = False is_relative = False else: dx, dy = d.split(",") dx = float(dx) dy = float(dy) if is_move_to: x = dx y = dy is_move_to = False else: if is_relative: x += dx y += dy else: x = dx y = dy points.append(complex(x, y)) return points
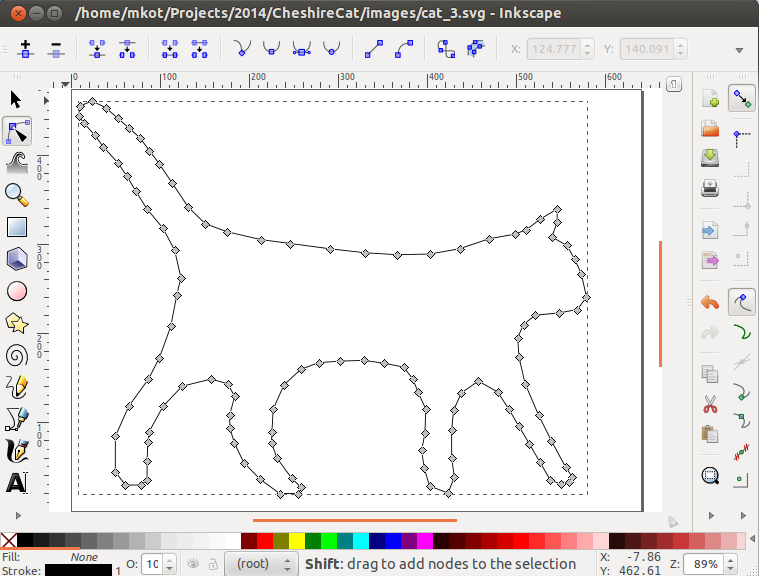
次に、外部から外部へのマッピングが必要です。パッケージは内部から内部へのマッピングを見つけます。 ここでは、生成されたディスプレイを反転とペアにする必要があります。 つまり、φ '(
z )= 1 /ψ(1 /
z )です。ここで、ψはパケットを生成するマップです。 そして、パケットの入力は、既に反転して送信されている必要があります。
一致 def invert_points_1(points, epsilon): inverted_points = [] for point in points: inverted_points.append(1 / ((1 + epsilon)*point)) return inverted_points def invert_points_2(points, shift): inverted_points = [] for point in points: inverted_points.append(1 / point + shift) return inverted_points if __name__ == "__main__": ... inverted_points = invert_points_1(points, epsilon) transformed_points = transform_points(inverted_points) inverted_transformed_points = invert_points_2(transformed_points, shift)
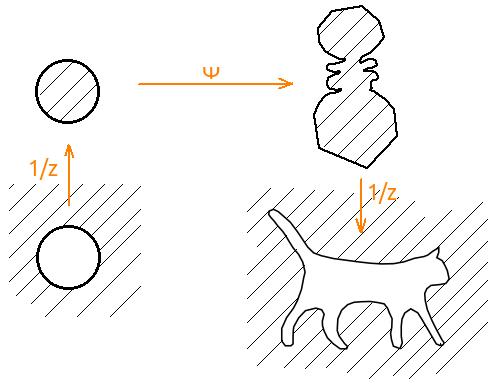
係数
cは、まだ多項式
fの定義に関係しています。 その値のおおよその計算には、次のトリックを使用します。 させる
f (
z )=
c z +
a +
a 1 /
z +
a 2 /
z 2 +
a 3 /
z 3 + ...
このシリーズのいくつかの有限であるが、かなり大きい部分を検討してください。 n次の単一性の根の値を代入します。ここで、
nはこの部分のメンバーの数よりも大きくなります。
f (
e2πik / n )=
c e2πik / n +
a +
a 1 e
−2π ik / n +
a 2 e-
4πik / n +
a 3 e
−6π ik / n + ...、
k = 0、...、
n -1。
次に、各行にe-
2πik / nを乗算し、すべての行を追加します。 単一性のすべての根の合計は0なので、
n cのみが右側に残ります。 したがって、私たちは置くことができます
c =(
f (1)⋅1 +
f (
e2πi / n )e
−2π i / n + ... +
f (
e2πi( n -1)/ n )e
−2π i ( n -1)/ n ))/
n 。
すべてをまとめて、何が起こったかを確認します。 以下の図は、モジュール
f (
z )の対数の「熱」グラフを示しています(赤は値が大きいほど)。 ご覧のとおり、猫の内部では多項式の値は小さく、猫の外部では多項式が増加します。 また、f(
e2πik / n )値の分布(緑色の点)にも注目してください。この効果のため、足が十分に離れている猫を描く必要がありました。

ここで、いくつかのアルゴリズムを使用してジュリアセットを描画し、境界がフラクタルな猫を取得します。
たとえば、暴走アルゴリズム def get_value(points, z, radius): result = 1 for point in points: result *= (z - point) / radius return z * (1 + result) def get_radius(points): n = len(points) result = 0 for k in range(n): result += points[k] * cmath.exp(-2j*math.pi*k/n) return result / n def draw_fractal(image, points, scale, shift, bound, max_num_iter, radius): width, height = image.size draw = ImageDraw.Draw(image) for y in range(0, height): for x in range(0, width): z = (complex(x, y) - shift) * scale n = 0 while abs(z) < bound and n < max_num_iter: z = get_value(points, z, radius) n += 1 if n < max_num_iter: color = ((100 * n) % 255, 128 + (50 * n) % 255, 128 + (75 * n) % 255) draw.point((x, y), color)

画像が複数の領域
A 1 、
A 2 、...、
A qで構成されている場合、上記の記事では、以下のように定義された多項式の代わりに有理マップ
f (
z )を使用することを提案します。 各領域
A rについて、上記のように積ωr(
z )を書きます。 次に、目的の有理関数
f (
z )は、式
f (
z )=
z /(1 /ω1(
z )+ ... + 1 /ωq(
z ))によって決定されます。
例えば、
イェの霧の中にハリネズミを飼いましょう。

ハリネズミと丘を一周します(丘の下の境界線は写真の外側にあります)。

真空のハリネズミ。

ハリネズミのない丘。

すべて一緒に。

ハリネズミのノミと拡大したハリネズミの腹。

いつものように、ソースコードは
githubにあります。
もう一度、すべてが判明した記事へのリンクを繰り返します:
Kathryn A. Lindsey 、
「Shapes of Polynomial Julia sets」 、2013、
arXiv:1209.0143 この記事は読みやすいので、証拠をお茶で分類できます。
楽しかったと思います。