会話を続けます。
前回は、単純ベイズ分類器からLDAへの移行の第一歩を踏み出しました。単純ベイズからトレーニングセットをマークする必要がなくなり、EMアルゴリズムで学習できるクラスタリングモデルになりました。 今日、これ以上言い訳はありません。LDAモデル自体について話し、それがどのように機能するかを示す必要があります。 このブログでLDA
について話しましたが、その話は非常に短く、重要な詳細はありませんでした。 今回、もっとはっきりと話せるようになることを願っています。
LDA：直観
それで、LDAについての会話を始めています。 一般化の主な目的は、ドキュメントが1つのトピックに厳密に結び付けられないようにし、ドキュメント内の単語が複数のトピックから一度に来ることを確認することです。 これは（数学的な）現実ではどういう意味ですか？ これは、ドキュメントがトピックの
混合物であり、各単語がこの混合物のトピックの1つから生成できることを意味します。 簡単に言えば、最初にドキュメントキューブをスローし、
各単語のトピック
を決定してから、対応するバッグから単語を引き出します。
したがって、モデルの主な直観は次のようになります。
- 世界には、ドキュメントのどの部分に関するものかを反映するトピック （以前は不明）があります。
- 各トピックは単語の確率分布です。 異なる確率で異なる単語を引き出すことができる単語の袋。
- 各ドキュメントはトピックの混合物です。つまり、 トピックに関する確率分布、スロー可能なキューブ。
- 各単語を生成するプロセスは、まずドキュメントに対応する分布によってトピックを選択し、次にこのトピックに対応する分布から単語を選択します。
直観は最も重要なことであり、ここでは最も単純ではないため、もう一度同じことを繰り返します。 生成プロセスの形で確率モデルを理解して表現すると、1つのデータ単位がどのように生成されるかを連続的に説明し、このモデルで行うすべての確率的仮定を導入するのに便利です。 したがって、LDAの生成プロセスでは、各ドキュメントの各単語を生成する方法を一貫して記述する必要があります。 そして、これがどのように起こるかです（以降、各ドキュメントの長さが指定されていると仮定します-モデルに追加することもできますが、通常は新しいものは何も提供しません）：
- 各トピックtについて ：
- 分布に従ってベクトルφt （トピック内の単語の分布）を選択する
;
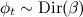- 各文書dについて ：
- ベクトルを選ぶ
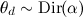-このドキュメントの各トピックの「表現度」のベクトル。 - 文書wの各単語に対して：
- 配布ごとにz zトピックを選択
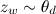; - 言葉を選ぶ
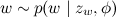βで与えられた確率で。
ここで、与えられた
θと
φの単語を選択するプロセスは、読者にはすでに明確になっているはずです。単語ごとにキューブをスローし、単語のトピックを選択してから、対応するバッグから単語を引き出します。
モデルでは、これらの
θと
φがどこから来て、表現が何を意味するかを説明するだけです
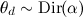
; 同時に、これがディリクレ割り当てと呼ばれる理由を説明します。
ディリクレはそれと何の関係があるのですか？
ヨハン・ピーター・グスタフ・レジューヌ・ディリクレは確率論にそれほど関与していませんでした。 彼は主に数学的分析、数論、フーリエ級数、および他の同様の数学を専門としていました。 確率理論では、彼はそれほど頻繁に見られませんでしたが、もちろん、確率理論での彼の結果は現代数学の素晴らしいキャリアを作ったでしょう（木はより緑で、科学はあまり研究されておらず、特に数学的なクロンダイクも使い果たされていませんでした）。 しかし、彼の数学的分析の研究では、特にディリクレは、そのような古典的な積分をとることに成功し、結果としてディリクレ積分と呼ばれていました。
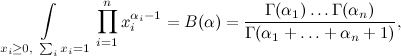
ここで、Γ（αi）はガンマ関数、階乗の継続（自然数の場合）
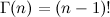
） ディリクレ自身が天体力学の必要性のためにこの積分を導き出し、その後、リウヴィルはより単純な結論を見つけました。それはより複雑な形式の被積分関数に一般化され、すべてをまとめました。
ディリクレ積分によって動機付けられたディリクレ分布は、次の方法で与えられた（
n -1）次元ベクトル
x 1 、
x 2 、...、
x n -1上の分布です。
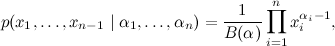
どこで
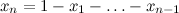
、および分布は（
n -1）次元シンプレックスでのみ与えられます。ここで、
x i > 0です。 それから、ディリクレ積分に正規化定数が現れました。 そして、ディリクレ分布の意味はかなりエレガントです-これは
分布上の分布です。 ルック-ディリクレ分布にベクトルを投げた結果、非負の要素を持つベクトルが得られ、その合計は1 ... bahですが、これは離散確率分布であり、実際には
n面の不正な立方体です。
もちろん、これは離散確率に関する唯一の可能なクラスの分布ではありませんが、ディリクレ分布には他にも多くの魅力的な特性があります。 主なことは、それがその非常に不正なキューブの
先験的分布の共役であることです。 これが何を意味するかについては詳しく説明しませんが（おそらく後で）、一般に、変数として不公平なキューブを取得したい場合は、確率モデルのアプリオリ分布としてディリクレ分布を使用するのが妥当です。
実際、αiの異なる値に対して何が得られるかを議論することは残っています。 まず、すべてのαi
が同じである場合に限定します。先験的には、一部のトピックを他のトピックよりも優先する理由はありません。プロセスの開始時点では、どのトピックが目立つかはまだわかりません。 したがって、分布は対称になります。
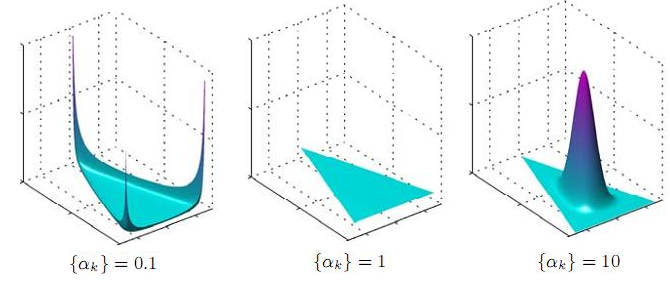
それはどういう意味ですか？シンプレックスでの配布ですか？ どのように見えますか？ これらの分布のいくつかを描画してみましょう-シンプレックスが2次元になるように3次元空間で最大値を描画できます-三角形、単純に入れて、-分布はこの三角形の上にあります（写真は
ここから撮影さ
れます ;原則として、そこで議論されていることは明らかですが、それは非常に興味深いです）ユニフォーム（0,1）がPandoraのボックスの下に署名されている理由-誰かが理解できたら、教えてください:)）：
ただし、ヒートマップの形式の2次元形式での同様の分布（たとえば、
ここで説明でき
ます ）。 確かに、ここでは0.1は完全に見えないので、0.995に置き換えました。
これが起こることです：α= 1の場合、均一な分布が得られます（これは論理的です-密度関数のすべての次数はゼロに等しい）。 αが1よりも大きい場合、αがさらに増加すると、分布はシンプレックスの中心にますます集中します。 αが大きい場合、ほぼ常にほぼ完全に正直なキューブが得られます。 しかし、ここで最も興味深いのは、αが1未満の場合に発生することです。この場合、分布は、シンプレックスのコーナーとエッジ/サイドに集中します。 言い換えれば、小さなαについては、
スパースキューブ-ほぼすべての確率がゼロに等しいか、ゼロに近く、それらのごく一部のみが実質的にゼロでない分布を取得します。 これはまさに私たちが必要とするものです-そして、ドキュメントでは、いくつかの実質的に表現されたトピックを見たいと思います。そして、トピックは、単語の比較的小さなサブセットを明確に概説するのに良いでしょう したがって、LDAは通常、ユニティ未満のハイパーパラメーターαおよびβを取ります。通常は、α= 1 /
T （トピック数の逆数）およびβ= Const /
W （50または100のような定数を単語数で割ったもの）です。
免責事項：私のプレゼンテーションは、LDAへの最も単純で最も単純なアプローチに従っています。私は、モデルの一般的な理解を伝えるために大きなストロークで試みています。 実際、当然ながら、ハイパーパラメーターαおよびβの選択方法、それらが与えるもの、および導くものに関するより詳細な研究があります。 特に、ハイパーパラメーターは対称である必要はありません。 たとえば、Wallach、Nimho、McCallumの記事「
LDAの再考：事前確率が
重要な理由 」を参照してください。
LDA：グラフ、共同分布、因数分解
簡単な要約を要約します。 モデルのすべての部分については既に説明しました-Dirichletのアプリオリ分布はドキュメントキューブとトピックバッグを生成し、ドキュメントサイコロを投げることで各単語のテーマを決定し、対応するトピックバッグから単語自体を選択します。 正式に言えば、グラフィックモデルは次のようになります。
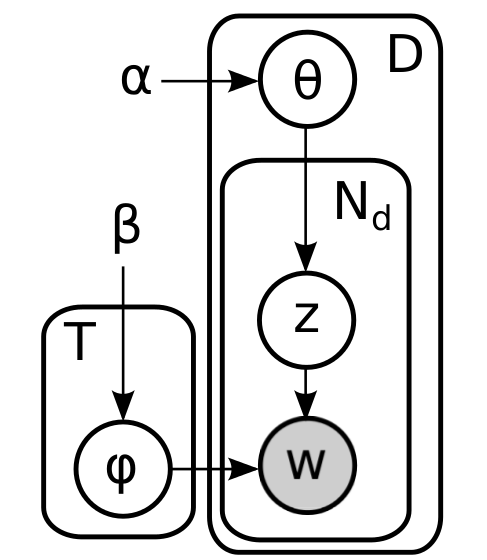
ここで、内側のプレートは1つのドキュメントの単語に対応し、外側のプレートはケースのドキュメントに対応します。 この図の単純な外見に惑わされる必要はありません。ここでのサイクルは十分です。 たとえば、2つのドキュメント（1つには2つの単語があり、残りの3つにはドキュメントがある）の完全に展開された因子グラフ
そして、共同確率分布は次のように因数分解されます。
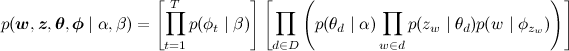
今LDAモデルを教えるタスクは何ですか？ 言葉だけが与えられ、他には何も与えられなかったことがわかり、これらのパラメーターのすべてをすべて訓練する必要があります。 タスクは非常に怖いように見えます-何も知られていないため、ドキュメントのセットからすべてを引き出す必要があります。
それにもかかわらず、それは以前に話した近似推論のまさにその方法を使用して解決されます。 次回、この問題を解決する方法について説明します。ギブスサンプリング法（
以前のインストールのいずれかを参照）をLDAモデルに適用し、変数
z wの更新方程式を導きます。 実際、この恐ろしい数学はすべてそれほど怖くないわけではなく、LDAは概念的にだけでなくアルゴリズム的にも理解しやすいことがわかります。