 スキップリストは、バランスの取れたツリーの代わりに使用できるデータ構造です。 バランスアルゴリズムは厳密ではなく確率的であるため、スキップされたリストでの要素の挿入と削除は、バランスツリーよりもはるかに簡単で高速です。
スキップリストは、バランスの取れたツリーの代わりに使用できるデータ構造です。 バランスアルゴリズムは厳密ではなく確率的であるため、スキップされたリストでの要素の挿入と削除は、バランスツリーよりもはるかに簡単で高速です。スキップリストは、バランスの取れたツリーの確率的な代替手段です。 乱数ジェネレーターを使用してバランスが取られています。 スキップのあるリストは最悪の場合パフォーマンスが低下するという事実にもかかわらず、常に発生するような操作のシーケンスはありません(サポート要素をランダムに選択するクイックソートアルゴリズムのように)。 このデータ構造が大幅に不均衡になることはほとんどありません(たとえば、250要素よりも大きい辞書の場合、検索に100万分の1未満の予想時間の3倍の確率がかかります)。
データ構造のバランスを取ることは、おそらく明示的にバランスを取るよりも簡単です。 多くのタスクでは、スキップリストはツリーよりも自然なデータ表現です。 アルゴリズムは実装が簡単で、実際には、バランスの取れたツリーよりも高速です。 さらに、スキップリストはメモリを非常に効率的に使用します。 それらは、平均で約1.33(またはそれ以下)のポインターが1つの要素に収まり、各要素のバランスや優先度に関する追加情報を必要としないように実装できます。
リンクリスト内のアイテムを検索するには、各ノードを調べる必要があります。

リストがソートされて保存され、その2番目のノードごとにさらに2つのノードへのポインターが含まれている場合、If
n /2⌉+ 1ノード(
nはリストの長さ)を超えないようにする必要があります。

同様に、4番目のノードごとに4つ先のノードへのポインターが含まれている場合、⌈n /4⌉+ 2ノード以下を調べる必要があります。

2
i番目のノードごとに前方に2
i個のノードへのポインターが含まれている場合、表示する必要があるノードの数は⌈log2 n⌉に削減され、構造内のポインターの総数は2倍になります。

このデータ構造はクイック検索に使用できますが、ノードの挿入と削除は遅くなります。
上流要素へのkポインタを含むノードを
レベルkのノードと呼びます。 2
i番目のノードごとに2
iノード前方へのポインターが含まれる場合、レベルは次のように分散されます。ノードの50%-レベル1、25%-レベル2、12.5%-レベル3など。 しかし、ノードレベルが同じ比率でランダムに選択された場合はどうなりますか? たとえば、次のように:

各ノードのポインター番号
iは 、レベル
i以上の次のノードを参照し、以前のように正確に2
i -1ノード前方ではありません。 挿入と削除には、ローカルの変更のみが必要です。 挿入時にランダムに選択されたノードレベルは変更されません。 レベルが正しく割り当てられていない場合、パフォーマンスが低下する可能性がありますが、そのような状況はまれであることを示します。 これらのデータ構造は、中間ノードをスキップするための追加のポインターを持つリンクリストであるという事実のため、私はそれらを
スキップリストと呼び
ます 。
運営
スキップされたリストに実装された辞書の要素を検索、挿入、削除するためのアルゴリズムについて説明します。
検索操作は、指定されたキーの値を返すか、キーが見つからなかったことを通知します。
挿入操作は、キーを新しい値に関連付けます(以前にキーがなかった場合はキーを作成します)。
削除操作によりキーが削除されます。 「最小キーの検索」や「次のキーの検索」など、このデータ構造に操作を簡単に追加することもできます。
リストの各要素は、ノードが作成されたときにレベルがランダムに選択されたノードであり、すでに存在する要素の数に関係ありません。 レベル
iノードには、1から
iまでのインデックスが付けられた前のさまざまな要素への
iポインターが含まれて
います。 ノード自体にノードレベルを保存することはできません。 レベルの数は、事前に選択された
MaxLevel定数によって制限されます。
リストレベルをこのリストの最大ノードレベルと呼びます(リストが空の場合、レベルは1です)。 リスト
の見出し (左側の図)には、レベル1から
MaxLevelへのポインターが含まれています。 このレベルの要素がまだない場合、ポインター値は特別なNIL要素です。
初期化
リストに表示される可能性のあるキーよりも大きいキーを持つNIL要素を作成します。 NIL要素は、スキップされたリストをすべて完了します。 リストレベルは1で、ヘッダー内のすべてのポインターはNILを参照します。
要素検索
最高レベルのポインターから始めて、目的の要素を超えない要素を参照するまで、ポインターに沿って進みます。 次に、1つ下のレベルに移動し、同じルールに従って再び移動します。 レベル1に達してさらに先に進むことができない場合は、探している要素の前にいます(存在する場合)。
検索 (リスト、searchKey)
x:=リスト->ヘッダー
#ループ不変式:x→キー<searchKeyfor i:=リスト→レベル
ダウン 1
dox→進む[i]→キー<searchKey
dox:= x→フォワード[i]
#x→キー<searchKey≤x→フォワード[1]→キーx:= x→フォワード[1]
x→キー= searchKeyの
場合、 x→値を
返します
それ以外の場合は失敗を
返し ますアイテムの挿入と削除
ノードを挿入または削除するには、検索アルゴリズムを使用して、挿入(または削除)される前のすべての要素を検索し、対応するポインターを更新します。
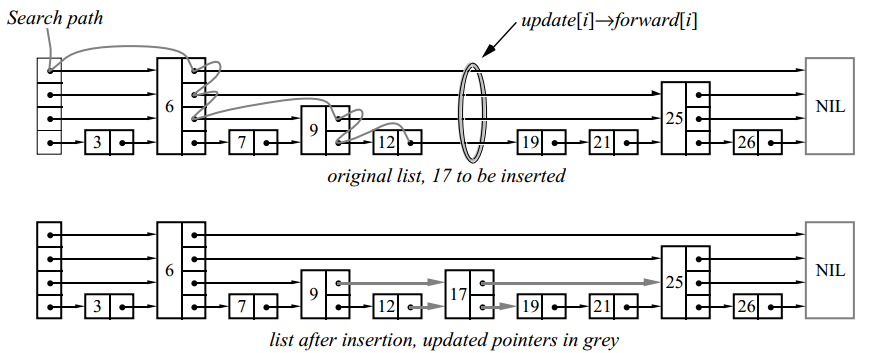 この例では、レベル2の要素を挿入しました。挿入
この例では、レベル2の要素を挿入しました。挿入 (リスト、searchKey、newValue)
ローカル更新[1..MaxLevel]
x:=リスト->ヘッダー
for i:=リスト→レベル
ダウン 1
dox→進む[i]→キー<searchKey
dox:= x→フォワード[i]
#x→キー<searchKey≤x→進む[i]→キー更新[i]:= x
x:= x→フォワード[1]
x→キー= searchKeyの
場合、 x→値:= newValue
他にlvl:= randomLevel()
lvl>リスト→レベル
for i:=リスト→レベル+ 1
から lvl
do更新[i]:=リスト→ヘッダー
リスト→レベル:= lvl
x:= makeNode(lvl、searchKey、value)
for i:=レベル1
x→転送[i]:=更新[i]→転送[i]
更新[i]→転送[i]:= x
削除 (リスト、searchKey)
ローカル更新[1..MaxLevel]
x:=リスト->ヘッダー
for i:=リスト→レベル
ダウン 1
dox→進む[i]→キー<searchKey
dox:= x→フォワード[i]
更新[i]:= x
x:= x→フォワード[1]
x→key = searchKeyの
場合for i:=リストするには1 =レベル
更新[i]→転送[i]≠xの
場合、 ブレーク更新[i]→転送[i]:= x→転送[i]
無料(x)
一方、リスト→レベル> 1
およびリスト→ヘッダー→転送[リスト→レベル] = NIL
doリスト→レベル:=リスト→レベル-1
挿入(または削除)配列の前の要素を記憶するために、
更新配列が使用されます。
更新[i]要素は、更新場所の左の番号から右端のノード(レベル
i以上)へのポインターです。
挿入されたノードのランダムに選択されたレベルがリスト全体のレベルよりも大きいことが判明した場合(つまり、そのようなレベルのノードがまだない場合)、リストのレベルを上げ、ヘッダーへのポインターで
更新配列の対応する要素を初期化します。 削除するたびに、最大レベルのノードを削除したかどうかを確認し、削除した場合はリストのレベルを下げます。
レベル番号の生成
前に、レベル
iポインターを含むノードの半分にレベル
i +1ノードへのポインターも含まれる場合のノードレベルの分布を示しました。 マジック定数1/2を取り除くには、レベル
iのノードへのポインターを含むレベル
iのノードの割合を
pで示します。 新しい頂点のレベル番号は、次のアルゴリズムを使用してランダムに生成されます。
randomLevel ()
レベル:= 1
#random()は、半区間[0 ... 1)で乱数を返しますランダム()<p
および lvl <MaxLevel
dolvl:= lvl + 1
レベルを
返すご覧のとおり、リスト内の要素の数は生成に関係していません。
どのレベルを探し始めますか? L(n)の定義
p = 1/2で生成された16要素のギャップがあるリストでは、レベル1の9要素、レベル2の3要素、レベル3の3要素、およびレベル14の1要素が含まれていることがあります(これは可能性は低いですが可能です) 。 これに対処するには? 標準のアルゴリズムを使用し、レベル14から検索する場合、多くの無駄な作業を行います。
どこで検索を開始する方が良いですか? 私たちの研究では、レベル
Lで検索を開始することが最善であることが示されています。レベル
Lでは、1 /
pノードが期待されます。 これは、
L = log
1 / p nのときに起こります。 さらなる議論の便宜上、関数log
1 / p nを
L (
n )として示します。
予想外に大きなノードの問題を解決するには、いくつかの方法があります。
- 蒸気を発しないでください (元は気にしないで、幸せになってください)。 リストにある最高レベルから検索を開始してください。 後で見るように、 n個のアイテムのリストのレベルがL(n)よりもかなり高い確率は非常に小さいです。 このようなソリューションでは、予想される検索時間に小さな定数のみが追加されます。 このアプローチは、上記のアルゴリズムで使用されます。
- 必要以上のスペースを使用しないでください。 要素には14個のポインターを含めることができますが、14個すべてを使用する必要はありません。そのうちのL(n)のみを使用できます。 これを実装する方法はいくつかありますが、それらはすべてアルゴリズムを複雑にし、パフォーマンスの顕著な向上につながりません。 この方法の使用は推奨されません。
- キューブを修正します。 リスト内のノードの最大レベルより大きいレベルが生成された場合、それは正確に1以上であると単純に信じています。理論上、実際には、これはうまく機能しているようです。 しかし、このアプローチでは、アルゴリズムの複雑さを分析する能力を完全に失います。 ノードレベルは完全にランダムではなくなりました。 プログラマーはこの方法を自由に使用できますが、理論家はそれを避けたほうがよいでしょう。
MaxLevelの選択
予想されるレベル数はL(n)であるため、
MaxLevel =
L (
N )を選択するのが最善です。ここで、
Nはスキップリストの要素の最大数です。 たとえば、
p = 1/2の場合、
MaxLevel = 16は2
16未満の要素を含むリストに適しています。
アルゴリズム分析
検索、挿入、および削除の操作では、適切なアイテムを見つけるのに最も時間がかかります。 挿入および削除するには、挿入または削除されたノードのレベルに比例して追加の時間が必要です。 要素の検索時間は、検索プロセスで渡されたノードの数に比例し、ノードのレベルの分布に依存します。
確率論的哲学
ギャップリストの構造は、このリストの要素数と乱数ジェネレーターの値によってのみ決定されます。 リストを取得する操作の順序は重要ではありません。 ユーザーはノードのレベルにアクセスできないと想定します。そうでない場合、ユーザーはアルゴリズムを最悪の時間動作させ、レベルが1以外のすべてのノードを削除できます。
同じデータ構造での順次操作の場合、実行時間は独立したランダム変数ではありません。 同じ要素を検索する2つの連続した操作には、まったく同じ時間がかかります。
予想検索時間の分析
検索中に最後から横断したパス、つまり 左上に移動します。 リスト内のノードのレベルは検索時に既知であり、固定されていますが、ノードのレベルは、最後から移動するときにノードのレベルに達したときにのみ決定されると想定しています。
パス上の任意の時点で、次の状況にあります。

ノード
xの i番目のポインターを見て、
xの左側にあるノードのレベルを知りません。 また、
xの正確なレベルはわかりませんが、少なくとも
iでなければなりません。
xがリストの見出しではないと仮定します(これはリストが左に無限に展開していると仮定するのと同じです)。 レベル
xが
iの場合、状況
bになります。 レベル
xが iより大きい場合、状況
cになります。 状況
cにある確率は
pです。 これが発生するたびに、1レベル上に移動します。
C (
k )を
k回上に移動したときの戻り検索パスの予想される長さとします。
C (0)= 0
C (
k )=(1-
p )(
シチュエーションbの経路長 )+
p (
シチュエーションcの経路長 )
簡素化:
C (
k )=(1-
p )(1 +
C (
k ))+ p⋅(1 +
C (
k -1))
C (
k )= 1 +
C (
k )-p⋅C(
k )+ p⋅C(
k -1)
C (
k )= 1 /
p +
C (
k -1)
C (
k )=
k /
pリストが無限であるという我々の仮定は悲観的です。 左端の要素に到達すると、左に移動するのではなく、常に上に移動します。 これにより、
n個の要素のリストで、レベル1のノードからレベル
L (
n )のノードまで
の予想パス長の上限(
L (
n )-1)/
pが得られます。
この推論を使用してレベル
L (
n )のノードに到達しますが、残りの方法では他の考慮事項が使用されます。 左への残りの移動の数は、リスト全体でレベル
L (
n )以上のノードの数によって制限されます。 そのようなノードの最も可能性の高い数は、1 /
pです。
また、レベル
L (
n )からリストの最大レベルに移動しています。 リストの最大レベルが
kより大きい確率は1-(1-p
k )
nであり、これはnp
k以下です。 予想される最大レベルは
L (
n )+ 1 /(1-
p )以下であると計算できます。 すべてをまとめると、
n個の要素のリストの検索パスの予想される長さを取得します
<=
L (
n )/
p + 1 /(1-
p )、
または
O (log
n )。
比較の数
検索したパスの長さがわかりました。 ユニットごとに必要な比較の数は、パスの長さを超えています(パスの各ステップで比較が行われます)。
確率的分析
さまざまな検索パスの長さの確率分布を考慮することができます。 確率分析はやや複雑です(元の記事の最後にあります)。 これにより、検索パスの長さが、指定された回数を超えて予想を超える確率を上から推定できます。 分析結果:
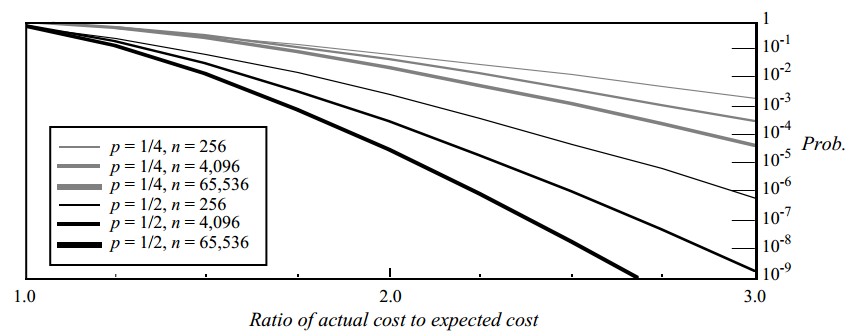 これは、操作が予想よりも大幅に長くかかる確率の上限のグラフです。 縦軸は、検索パスの長さが、パスの予想される長さよりも横軸で遅延した回数だけ長くなる確率を示しています。 たとえば、p = 1/2およびn = 4096の場合、結果のパスが予想より3倍長くなる確率は1 / 200,000,000未満です。
これは、操作が予想よりも大幅に長くかかる確率の上限のグラフです。 縦軸は、検索パスの長さが、パスの予想される長さよりも横軸で遅延した回数だけ長くなる確率を示しています。 たとえば、p = 1/2およびn = 4096の場合、結果のパスが予想より3倍長くなる確率は1 / 200,000,000未満です。Pの選択
この表は、正規化された検索時間と、さまざまな
p値に必要なメモリ量を示しています。
| p | 正規化された検索時間
(すなわち、正規化されたL ( n )/ p ) | ノードあたりのポインターの平均数
(つまり1 /(1- p )) |
|---|
| 1/2 | 1 | 2 |
| 1 / e | 0.94 ... | 1.58 ... |
| 1/4 | 1 | 1.33 ... |
| 1/8 | 1.33 ... | 1.14 ... |
| 1/16 | 2 | 1.07 ... |
pを小さくすると、操作の時間的広がりが大きくなります。 1 /
pが2のべき乗である場合、ランダムビットのストリームからレベル番号を生成すると便利です(生成には、平均で(log
2 1 /
p )/(1-
p )ランダムビットが必要です)。
L (
n )(ただし
L (
n )/
pではない)に関連するオーバーヘッドがあるため、
p = 1/4(1/2ではなく)を選択すると、アルゴリズムの複雑さの定数がわずかに減少します。
p = 1/4を選択することをお勧めしますが、操作時間の広がりが速度よりも重要な場合は、1/2を選択します。
複数の操作
操作のシーケンスの予想合計時間は、シーケンス内の各操作の予想時間の合計に等しくなります。 したがって、
n個の要素のデータ構造における
m回の検索操作のシーケンスの予想時間は
O (
m * log
n )です。 ただし、検索操作のパターンは、操作シーケンス全体の実際の時間の分布に影響します。
同じデータ構造で同じ要素を探すと、両方の操作にまったく同じ時間がかかります。 したがって、合計時間の分散(散布)は、1つの検索操作の分散の4倍になります。 2つの要素の検索時間が独立したランダム変数である場合、合計時間の分散は個々の操作の実行時間の分散の合計に等しくなります。 同じ要素を何度も検索すると、分散が最大化されます。
性能試験
スキップされたリストのパフォーマンスを他のデータ構造と比較します。 すべての実装は、最大のパフォーマンスのために最適化されています。
| データ構造 | 検索する | 挿入 | 削除する |
|---|
| リストをスキップ | 0.051ミリ秒(1.0) | 0.065ミリ秒(1.0) | 0.059ミリ秒(1.0) |
| 非再帰的なAVLツリー | 0.046ミリ秒(0.91) | 0.10ミリ秒(1.55) | 0.085ミリ秒(1.46) |
| 再帰的な2〜3本の木 | 0.054ミリ秒(1.05) | 0.21ミリ秒(3.2) | 0.21ミリ秒(3.65) |
| 自己制御ツリー: |
| 上から下へ拡大(トップダウンの広がり) | 0.15ミリ秒(3.0) | 0.16ミリ秒(2.5) | 0.18ミリ秒(3.1) |
| 下から上へ拡大(下から上へ) | 0.49ミリ秒(9.6) | 0.51ミリ秒(7.8) | 0.53ミリ秒(9.0) |
テストはSun-3 / 60マシンで実行され、2
16個の要素を含むデータ構造で実行されました。 括弧内の値は、省略されたリスト(時間単位)に対する相対時間です。 要素の挿入および削除のテストでは、メモリ管理(たとえば、mallocおよびfreeのC呼び出し)に費やされた時間は考慮されませんでした。
スキップされたリストには、他のデータ構造よりも多くの比較演算が必要であることに注意してください(上記のアルゴリズムでは、平均
L (
n )/
p + 1 /(1 +
p )演算が必要です)。 実数をキーとして使用すると、スキップリストでの操作はAVLツリーの非再帰的実装よりも若干遅くなり、スキップリストでの検索は2-3ツリーでの検索よりもわずかに遅くなりました(ただし、挿入と削除パスのあるリストでは、2〜3本のツリーを再帰的に実装するよりも高速でした。 比較操作が非常に高価な場合、アルゴリズムを変更して、目的のキーが他のノードのキーとノードごとに複数回比較されないようにすることができます。
p = 1/2の場合、比較回数の上限は7/2 + 3/2 * log
2 nです。
リクエストの不均等な分配
自己調整ツリーは、要求の不均等な分散に適応できます。 パスを持つリストは、自己調整ツリーよりもはるかに高速であるため、自己調整ツリーは、クエリの分散が非常に不均一な場合にのみ高速になります。 自己調整リストを省略して開発することはできましたが、これには実用的な意味がなく、元の実装の単純さとパフォーマンスを損ないたくありませんでした。 アプリケーションで不均一な要求が予想される場合、自己調整ツリーの使用またはキャッシュの追加が望ましいでしょう。
おわりに
理論的な観点から、スキップリストは必要ありません。 バランスのとれたツリーは、同じ操作を実行でき、最悪の場合(リストのスキップとは対照的に)複雑度が高くなります。 ただし、バランスの取れたツリーの実装は困難なタスクであり、その結果、大学での実験室作業を除いて、実際に実現されることはほとんどありません。
スキップリストは、ほとんどの場合、バランスの取れたツリーの代わりに使用できる単純なデータ構造です。 アルゴリズムの実装、拡張、変更は非常に簡単です。 スキップされたリストでの操作の従来の実装は、バランスの取れたツリーでの高度に最適化された実装とほぼ同じくらい速く、高度に最適化されていない通常の実装よりもかなり高速です。