👩🏼‍✈️ 👲🏼 👩🏿‍🎤 「論理回路の信頼性」のタスク 😢 🗒️ ⛵️

前文：スポーツプログラミングのほとんどのタスクは、独自の正しいソリューションによって判断されます。実際、競合するプログラムの発行と正解テンプレートを比較します。しかし、合理的な時間枠内で最良の解決策が不可能または非常に困難な問題の層があります。ただし、2つのソリューションは、いくつかのメトリックで簡単に比較できます。このため、検証プログラムは複雑ですが、独自のヒューリスティックな決定アルゴリズムを開発する範囲は拡大しています。私はあなたの裁判所にそのような仕事を提示します。

組み合わせ論理回路は、すべての最新のプロセッサおよびその他の電子情報処理ツールの一部です。プロセッサは普遍的に使用され、ますます複雑になっています。最新のプロセッサのトランジスタ数はすでに20億を超えてい^ますか？そして、成長は止まらないようです。同時に、プロセッサー生産の技術プロセスが削減されます。トランジスタは小さくなり、外部の影響を受けやすくなっています。そして今、最も強力な外部放射や磁場でさえ、マイクロ電子回路の論理値の短期的な変化をもたらすことはできません。この問題は、特に信頼性のための宇宙およびその他の重要なシステムに関連しています。この問題では、問題を提起します。 回路の論理的な目的を知って、どのようにして外部の影響に対する耐性を高めるのでしょうか？ あなたの仕事は、そのような安定したスキームを作成するためのアルゴリズムを開発することです。

フィードバックなしで、次の6つの要素で構成される論理図を示します。

役職	説明	運営
INV	インバーター	OUT =！A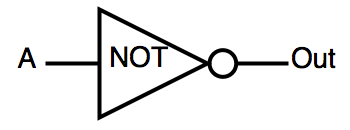
そして	論理的な「AND」	OUT = A＆B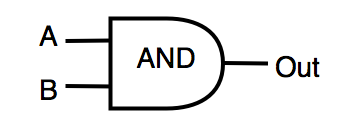
または	論理的な「OR」	OUT = A \| B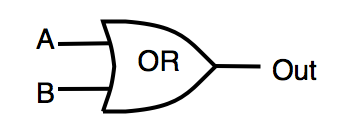
ナンド	逆AND	OUT =！（A＆B）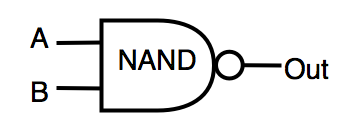
また	逆OR	OUT =！（A \| B）
Xor	排他的な「OR」	OUT = A ^ B

回路は環境ノイズの影響を受け、バルブの論理値が逆に変化する可能性があります。オリジナルと同じ論理機能を実行する回路を構築する必要がありますが、故障しにくいです。問題の状況に応じて、設計した回路は、元の面積の「 K 」倍以下でなければなりません。

論理回路の故障に対する安定性を特徴付けるパラメーターの1つはCOF- 「回路の一般的なエラー耐性」です。 COFは、実行されたテストの総数に対する、回路の正しい結果の数（回路のすべての出力に正しい値が必要）の比率として計算されます。したがって、最も信頼できるスキームでは、 COFは1になる傾向があります。

回路の各論理ゲートは、次のパラメーターによって特徴付けられます。Sはゲートの面積、 pは現在の外部条件下での故障の確率（％）です。

入力データ

最初の行は、番号Z-テストの数（ Z <400）を示しています。 Zテストが続きます。

各テストの最初の行は、数K （2.0≤K≤20.0）-エリア全体の回路の最大冗長性を示します。

次の6行は、それぞれ面積S （1≤S≤100）と故障の確率q （0≤q≤20）の2つの数値を示します。各論理要素のパラメーターは、INV、AND、OR、NAND、NOR、 XOR。

次の行は、数字「 I 」（0 < I <250）-回路の入力数、その後にスペースで区切られた20文字以内のI行-回路の入力ノードの名前を示します。

次の行は、数値「 O 」（0 < O <150）-回路出力の数、次にスペースで区切られた20文字以下のO行-回路の出力ノードの名前を示します。

以下は、 N回路の論理ゲートの数（1 < N <5000）であり、各ゲートの説明を含むN行が続きます。

各ゲートの説明はそのタイプで始まり、入力ノードの名前、出力ノードの名前が続きます

インプリント

テストごとに、回路の説明を次の形式で表示する必要があります。最初の行の数値N （1 < N <100000）は、結果の回路内のバルブの数です。この後には、 N-バルブの説明を含む行が続きます。各ゲートの説明は、そのタイプで始まり、入力ノードの名前、出力ノードの名前が続きます。

得点

スコアによって獲得されたポイントの数は、すべてのテストで要約されます。テストで受け取ったポイントの数は、スキームで計算されたCOF値と等しくなります。 COFはモンテカルロ法で計算され^ますか？ 2段階で：

1）最初の段階で、ジャッジプログラムは、回路が元の回路と同じように動作することを決定します。同じテストシーケンス（数千回）が両方の回路に入力され、回路出力の論理値が比較されます。論理値が異なる場合、間違った回答のステータスを受け取ります。

2）第2段階で、ジャッジプログラムは、指定された確率に従って回路のバルブの値をランダムに反転し、回路と標準回路の値を比較します。少なくとも1つの出力が異なる場合、「不正解」のカウンターが増加します。計算には、式COF =（ TT - INC ）/ TTが使用されます。ここで、
TT-少なくとも1つの埋め込みエラーがあるテストの数
INC-少なくとも1つの回路出力でエラーが発生したテストの数

裁判官プログラムは、回線の冗長性が指定された冗長性を超えていないことも検証します。

ソリューションの制限

プログラムのサイズは50 KB以下です
50秒以内に完了するまでの時間
40以上のプログラミング言語がサポートされています（C / C ++、Java、Pascalなど）

例

入力データ：

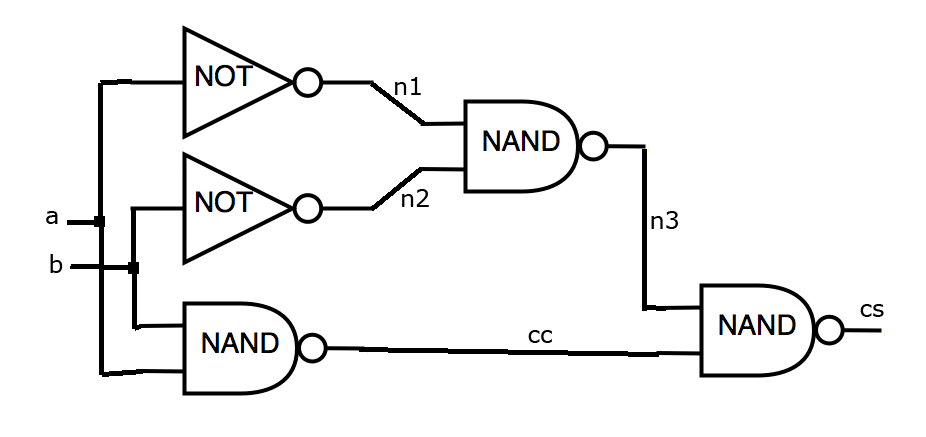
次のロジックを指定します（図を参照）。必要な冗長性は4.1倍を超えないようにしてください。このスキームは、次のライブラリで構築されます。

INVの面積は50で、故障確率は3％です

ANDの面積は60で、故障確率は3.1％です

ORの面積は60で、故障確率は3.2％です

NANDの面積は70で、故障確率は3.3％です

NORの面積は70で、故障確率は3.4％です

XORの面積は70で、故障率は3.5％です

このタスクの入力ファイルは次のようになります。

  1
 5.1
 50.0 3.0
 60.0 3.1
 60.0 3.2
 70.0 3.3
 70.0 3.4
 70.0 3.5
 2 ab
 2 cs cc
 5
 INV a n1
 INV b n2
ナンドab cc
 NAND n1 n2 n3
 NAND n3 cc cs

出力データ：

私たちのアルゴリズムに、より多くの出力で使用される論理値（Triple Modular Redundancy（TMR））を3倍して選択する標準的な手法を使用させ^ますか？。この場合、出力ファイルは次のように記述できます。

  25
 INV a n1_a0
 INV a n1_a1
 INV a n1_a2
 INV b n2_a0
 INV b n2_a1
 INV b n2_a2
 NAND ab cc_a0
 NAND ab cc_a1
 NAND ab cc_a2
 NAND n1_a0 n2_a0 n3_a0
 NAND n1_a1 n2_a1 n3_a1
 NAND n1_a2 n2_a2 n3_a2
 NAND n3_a0 cc_a0 cs_a0
 NAND n3_a1 cc_a1 cs_a1
 NAND n3_a2 cc_a2 cs_a2
 AND cs_a0 cs_a1 cs_3_0_and_0_out
 AND cs_a0 cs_a2 cs_5_0_and_0_out
 AND cs_a1 cs_a2 cs_6_0_and_0_out
またはcs_3_0_and_0_out cs_5_0_and_0_out cs_0_or_0_out
またはcs_0_or_0_out cs_6_0_and_0_out cs
 AND cc_a0 cc_a1 cc_3_0_and_0_out
 AND cc_a0 cc_a2 cc_5_0_and_0_out
 AND cc_a1 cc_a2 cc_6_0_and_0_out
またはcc_3_0_and_0_out cc_5_0_and_0_out cc_0_or_0_out
またはcc_0_or_0_out cc_6_0_and_0_out cc

出力ファイルの画像

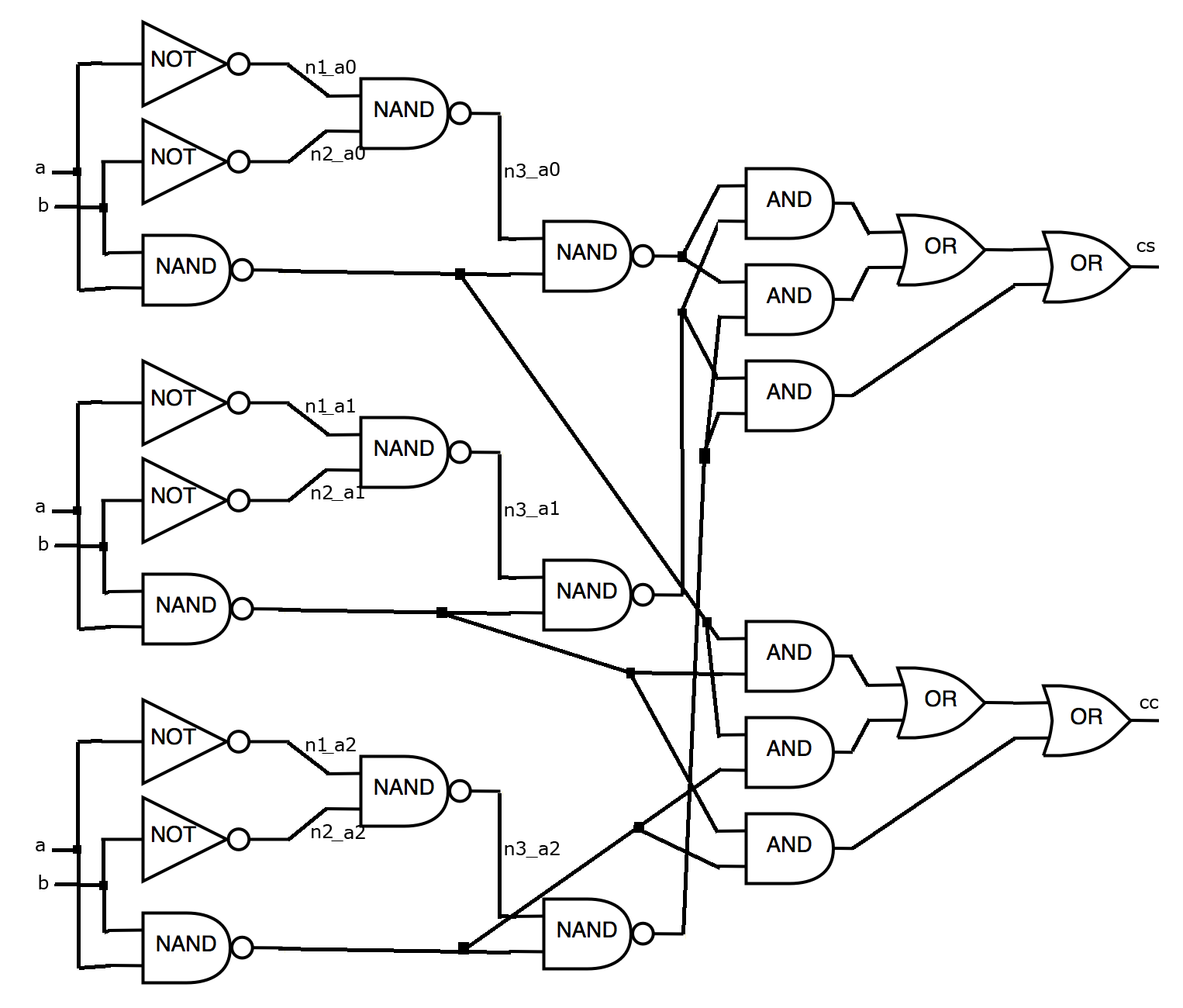
得点：

この決定には、シミュレーション後、0.682661ポイントが付与されます。

ソリューションの提出

決定を送信 *

送信済みソリューションテープ

最高のソリューション

*-送信するには、SPOJ（Shere Online Judge）システムのアカウント[ 登録 ]が必要です。

便利な資料

プログラムをゼロから作成しないために、既製の開発を使用できます。
1） C \ C ++の問題の簡単な解決策 -プログラムはデータを読み取り、回路を変更なしでそのまま表示します。
2） C \ C ++で判断 -問題の解決策を評価するためにサーバーで使用されるプログラム。ローカルで使用して、ソリューションの有効性をテストできます。
3）テストデータセット -サーバー上の閉じたセットに類似した102個のテスト回路のセット。

著者：Soloviev R.A.、Telpukhov D.V.

「論理回路の信頼性」のタスク