方程式または観察？

ピグレット：気分を良くしてください 、バグ、今日は自由落下体で精神実験を行っています。
バグ：それはどうですか？ 体は私の心に落ちますか？ 私はそれを直接見ます：星空を背景に飛んでいる裸の体...
リトルスポット：体はもちろん想像上のものですが、裸であるほど大きくはありません。 一般に、均一な重力場での物体の自由落下について話します。



バグ：これはどんな夢のプロジェクターですか？
ピグレット：これは私のパイロットプロジェクトです。 これまでのところ、これはバンドルにIPythonを使用した恐ろしいPythonコードの束です。 それでは、会話に戻りましょう。 だから、体は初速度で自由に落ちる 加速して動く...
バグ：繰り返しますが、あなたは自分自身にあらゆる種類の奇妙な呪いをつぶやいています。 飛んでいる蝶を何度も見ましたが、それを毎日喜んで食べています。 そして、あなたのプロジェクターは、あなたが異なる方向にたくさんのスペースのスランプを散らした場合に何が起こるかを示すことができますか？ 私は女性を怒らせる新しい方法を考えています...ごめんなさい、夕食を吸収します。
子豚：いつまでも食べ物について考える、バグ。 一般に、はい、そのような状況をモデル化できます。 すべてのピースが同じ速度で1つから飛び出し、最初の数秒で飛行を追跡すると仮定します。


バグ：うわー、敬礼！
ピグレット：本当ですか？ 他に何か気づいていますか？
バグ：うーん、ピースが円を形成しているように見えます...常に...好奇心の強い絵 なぜこれが起こっているのですか？
リトルスポット：説明する前に、これは計算や数式のない円であることを認識したことに注意してください。 プロジェクタでも、見た場合、ピースが常に円を形成する必要があることはどこにも示されていません。 たくさんの飛んでいるピースをエミュレートするようにプロジェクターに伝えただけで、すでにあなたの脳自体は、簡単な説明や公式のないパターンに気付きました。 主なことは、興味深い質問をして、そのようなプロジェクターを手に入れることです！

そして、今、私はそのような写真がなぜ出てくるのか説明しようとします。 あなたが残りと一緒に飛んでいる小さな破片の1人であると想像してください。 しかし、あなたはみんなと一緒に投げられたわけではなく、何とか逃げ出し、初速なしで巣から落ちました。 あなたの感覚に少し来て、あなたは周りを見回して、残りの部分を見ます。 彼らの行動はどのように見えると思いますか？
バグ：まあ、彼らは巣から追い出されたので、おそらく私から離れるでしょう。
ピグレット：そうです、自由に落ちるあなたに関連する基準の枠組みでは、重力は作用しません。つまり、破片はあなたから遠ざかり、同じ速度で均一に直線的に移動します。
バグ：うわー、どうやってまた賢く始めたの？ しかし、私は要点をつかみました：自転車のスポークのように、断片は私から逃げ出し、一般に、自転車の車輪のような円を形成します。 そして、これをプロジェクタで「見る」ことができますか？
ピグレット：できます。これは自宅でのエクササイズになります。 また、自由落下のための式を使用して、ピースが常に円を形成することを正式に証明しようとします。

バグ：わかりました、わかりました。 そして、あなたのプロジェクターで他に面白いものは何ですか？
ピグレット：通常の現象で奇妙な特性を見つける1つの秘trickについてお話しします。 一般に放物線に沿って自由落下体が動くことを覚えていますか？
バグ：だから、これはあなたがプロジェクターの星の近くに尾のようにそこに描いたものです！ はい、放物線についての何かが私の記憶にあります。
にきび：とても良い！ 百科事典で放物線の興味深い特性を見てみましょう。 最初に、飛行を上で賞賛した破片の軌跡の頂点にマークを付けた場合の写真を見てみましょう。
バグ：そして、ラベルを貼る場所をプロジェクターにどのように説明しますか？
ピグレット：ええと、これは2つの方法で行うことができます。 未知の現象を調査する場合、プロジェクタに軌跡の極大値を見つける方法を簡単に説明できます。 しかし、私たちは地球のフィールドで体がどのように動くかを知っているので、頂点座標の式を見つけようとし、同時にsympyパッケージがこれにどのように役立つかを見てみましょう。

 v_x = v_0 * cos(alpha) v_y = v_0 * sin(alpha) - g * t (Eq(Symbol('v_x'), v_x), Eq(Symbol('v_y'), v_y)) 

ヒント：ここで、ポイント（0,0）から起動した場合のピースの座標を計算します。 このためには、時間の経過とともに速度を統合する必要があります

 x_t = integrate(v_x, t) y_t = integrate(v_y, t) (Eq(x, x_t),Eq(y, y_t)) 

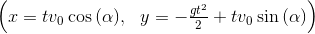バグ：待って、待って！ 少し混乱しました。 なぜSymbol（ 'v_x'）を書いているのですか？ 結果の方程式を見るためにv_x変数を指定できないのはなぜですか？ はい、あなたはどういうわけか奇妙な方程式を導き出します...
ピグレット：あなたは非常に注意深く、バグ、よくやった！ これは、v_x変数とv_x シンボルが異なるエンティティであるためです。 詳細はこちらをご覧ください 。
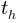
スポット：軌跡の上部、垂直速度 瞬間を見つける場所 これはいつ起こりますか。

 solution=solve(v_y, t) t_h = solution[0]; t_h 

リトルスポット：最後に、放物線の頂点の座標：

 x_h = x_t.subs(t, t_h);x_h 

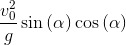
 y_h = y_t.subs(t, t_h);y_h 

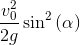ピグレット：プロジェクターにこの知識を教え 、何が起こるか見てみましょう。


バグ：気絶しました！ それは...それは...楕円だ！ まあ、非常に似ています！
少しスポット：よくやった、バグ。 気づいた、あなたは最初に絵を見ました、そして、脳自体はあなたがフォーミュラをどう見つめても気付かれないパターンを促しました。
バグ：ヒント、私はあなたがプロジェクタをいじっている理由を理解し始めているようです。 そして、これが本当に楕円であり、想像のフィクションではないことを証明しますか？
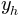
ピグレット：もちろん、やってみよう。 確かに、sympyに達成したいことを少し説明する必要があります。 実際、放物線の頂点の式で角度を取り除き、関連する式を取得する必要があります そして 。 額を決めようとする場合：

 solve([x-x_h, y-y_h], [y, alpha]) 

小さなスポット：アブラカダブラを取得します（自分で家を確認してください）。 そして、すべてsympyはまだ小さいため、三角関数式をエレガントに操作する方法を知りません。 しかし、私たちは彼を助けます。 開始するには：

 x_h = trigsimp(x_h); x_h 

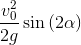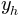
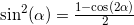
コンマ：次に、式で 交換することができます 。 置換を行い、以下を取得します。

 y_h = y_h.subs(sin(alpha)**2, (1-cos(2*alpha))/2);y_h 

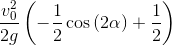バグ：あなたは平等を使いたいと言っている
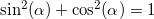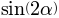
ピグレット：準備の長い夜があなたにとって無駄ではなかったことはすぐに明らかです。 表現する そして を通して そして 。

 s = solve([x-x_h, y-y_h], [sin(2*alpha), cos(2*alpha)]);s 

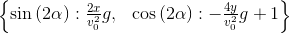ヒント：そして、あなたが気づいた平等に置き換えてください：

 Eq(s[sin(2*alpha)]**2 + s[cos(2*alpha)]**2, 1) 

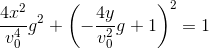ピグレット：楕円方程式しか得られません！
バグ：ええ...
ヒント：宿題のもう1つは、楕円の形状が初期速度とその中心の座標に応じてどのように変化するかを調べることです。トリックを調べることもできます。 ヒント：楕円の離心率を見つけます。 彼は、あなたが覚えているように、楕円の形状を決定します

バグ：わかりました、わかりました、あなただけが賢いのではありません。どういうわけかわかります。 何か他のものを見せた方がいいでしょう。そうでなければ、楕円を見つけて子供のように喜ぶでしょう...
ピグレット：そして、ここで見せます！ 上記の百科事典をさらに読み、放物線の焦点の説明を見つけます。 私たちの直接の質問は何ですか？ あなたの酸っぱい鉱山では、私たちがすべての放物線のトリックをマークし、何が起こるかを見たいとすぐに明確になります。
バグ：何、また楕円？
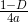
ピグレット：どうやって知るの？ 見てみましょう。 対称性の観点から、焦点の横座標は放物線の頂点の横座標と一致します。 しかし、縦座標は式で見つける必要があります 百科事典によると。 これを行うには、最初に放物線方程式を見つけます そして 、これを取り除く 。

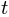
 ss = solve([x-x_t,y-y_t], [y,t], dict=True);ss 

スポット：したがって、二次三項係数：

 a,b,c = ss[0][y].as_poly(x).all_coeffs(); a,b,c 

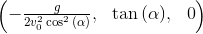ピグレット：それから自分で試してみてください。
バグ：それでは、判別式は次のようになります。

 D = b**2 - 4*a*c; D 

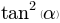バグ：およびフォーカス縦座標：

 y_f=(1-D)/(4*a);y_f 

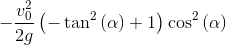バグ：これがあなたのプロジェクターZapyatochkaに置き換えられるとどうなりますか？
ピグレット：でも何だ！


バグ：言葉がありません！ 何かが神聖なサインのように見えます...私は覚えていました！ ラーの目！
ピグレット：まあ、想像力がありますよ、バグ。 トリックが円上にあることを証明してみてください？
バグ：それで、最初に単純化を試みます：

 y_f = trigsimp(y_f); y_f 

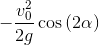バグ：ええ、それはここでうまくいきます！ 汗をかく必要はありません。横座標と縦座標の正方形を追加するだけです。

 Eq(x**2 + y**2, simplify(x_h**2 + y_f**2)) 

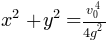ピグレット：まあ、あなたはとても素晴らしい仲間なので、ここにあなたのための別のパズルがあります。 私たちの放物線の監督の振る舞いを学びます。
バグ：それに問題がある場合はどうすればよいですか？
少しのスポット：自分で理解してみてください。私たちのツールはまだ完璧とはほど遠いことを思い出してください。 まだ質問がある場合は、再度会って話をします。

最後に、最後のタスク：会話の最初の最初の写真を注意深く見てください。背景にもう一人の人物が迫っていますか？ これがどのような図で、どのように動作するかを理解してください。

インスピレーションを得るためのリソースがさらに2つあります。

• JL Fernandez-Chapou et al。、 放物線軌道の楕円特性
• Dream Projector： ソースコード
• ブレットビクター、 上下のはしごの抽象化
• Bret Victor、 実用ツールとしてのシミュレーション