エド・ペグ・ジュニア投稿翻訳「 近くから完璧へ—三角形の問題 」
翻訳の手助けをしてくれたAndrei Dudinに感謝します。
翻訳はMathematicaドキュメントとしてダウンロードできます。このドキュメントには、記事で使用されているすべてのコードが含まれています。Wolfram言語 （Mathematicaなどでアクセス可能）では、
RootApproximant関数を使用すると、近似値の代数的数の形で閉じた形を見つけることができ、この関数により、正方形を角度（45°）の50個の同様の鋭角三角形に分割する問題の近似解を求めることができます、60°、75°）を正確に。
たとえば、単純に反対側の頂点を接続することにより、正方形を三角形に分割（三角形分割）できることは明らかです。 正方形は、サイズが異なる7つの類似した三角形または10個の
鋭角の二等辺三角形に分割できることも知られてい
ます （下図を参照）。 また、正方形を8つの鋭角三角形（下図を参照）に分割すること、または20の三角形に分割することに関連する古典的な問題もあります。
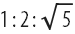
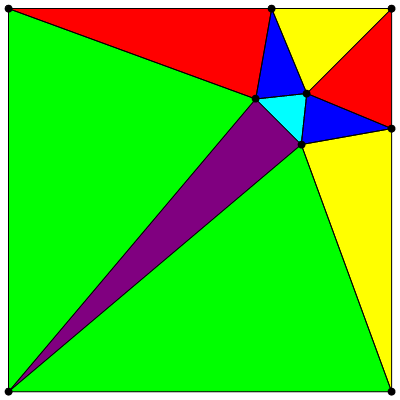
。 3番目の図（上から数えた図）は、正方形を角度（45°、60°、75°）の類似の三角形に分割したものを示していますが、三角形の一方が他方とわずかに重なっているため、この解決策が正しくないことがすぐにわかります。
[1]で：=
アウト[9] =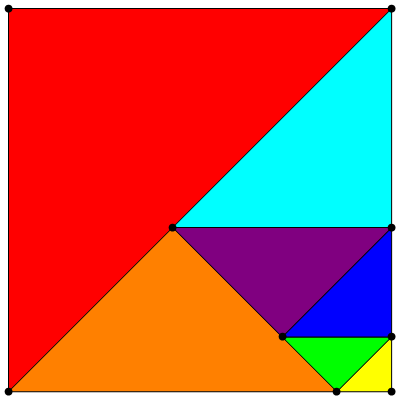
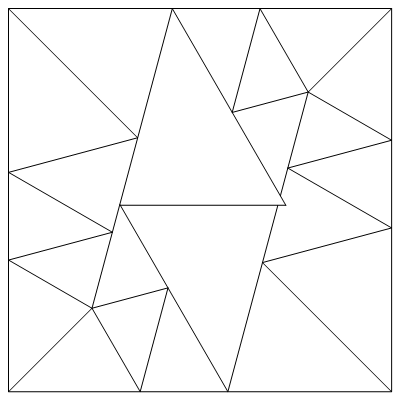
正方形のパーティションを同様の直角三角形に簡単に見つけることができます。 しかし、正方形を同様の非長方形の三角形に分割することは可能ですか？
Laczkovichは 、記事「
類似の三角形を備えたポリゴンのタイル 」（
Combinatorica 、10（3）、1990 pp。281–306）で、これは3種類の三角形でのみ可能であることを証明しました。角度付き（22°30 '、45°、112°30'）、（15°、45°、120°）および（45°、60°、75°） 私はこの記事を読んで、正方形の角度（45°、60°、75°）を持つ同様の三角形へのパーティションを明示的に見つけようとしましたが、そのようなパーティションの構築は困難であることが判明し、この問題を解決するには何千もの時間がかかると感じました三角形。 私のすべての決定には上記のような欠陥が含まれていたため、小さな
競争を組織することにしました。見つかったパーティションの報酬は、見つかったソリューションの各三角形の200ドルマイナス1ドルです。
ルーバクスターは、ラスコビッチのアプローチを徹底的に研究することから始め、
7 兆個の三角形を使用して解決策を見つけることができました。 しかし、彼はこのソリューションを改善する方法を見つけ、より最適なソリューションを検索するプログラムを作成しました。 数週間以内に、彼は198個の三角形を含むソリューションを受け取りました。これは私から賞金2ドルを得るのに十分でしょう。 しかし、彼は検索を続け、最終的に64個の三角形のみを含むソリューションに到達しました。 残念ながら、三角形のすべての頂点の座標は、非常に正確ではありますが、ほぼ見つかりました。 その時、私が以下に示す解決策は最適であり、閉じた形でもより良い解決策を見つけることは不可能であると思われました。 下の図では、見つかった正方形の半分のパーティションを見ることができます。元の問題の解決策を得るには、正方形の対角線に対してこの解決策を反映するだけで十分であることは明らかです。
[10]で：=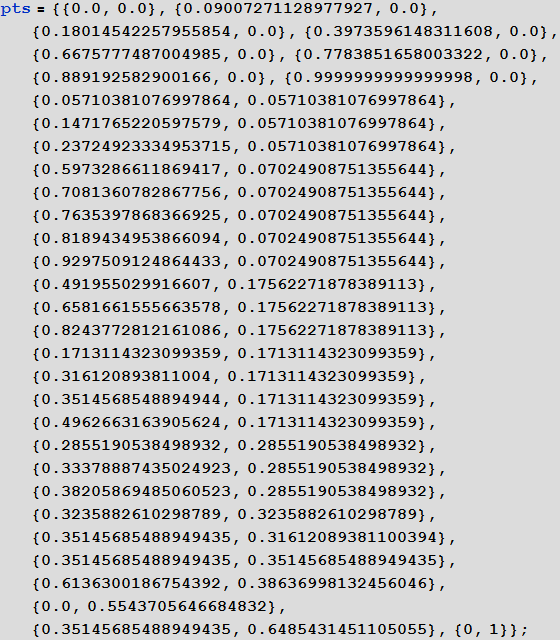
[11]で：=
[12]で：=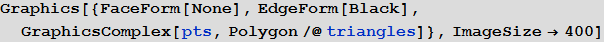
アウト[12] =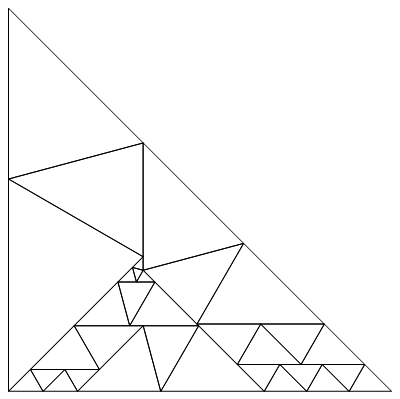
この近似解の正確な解を作成するには、RootApproximant関数を使用します。これは、この近似数を所定の精度で近似する多項式の根を検索します。 私たちが検討しているような幾何学的問題では、多くの場合、正確な解はいくつかの多項式の根の集合にすぎません。 問題の問題について、私は次のことを試しました：RootApproximant関数を使用して、各座標に閉じた形が見つかり、分数を取り除くために4686を掛けました。 すべての値は、フォームを持っていることが簡単にわかります
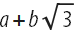
それはかなり励みに思えます。
[13]で：=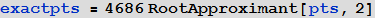
アウト[13] =
以下に、64個の三角形を含む結果のソリューションを示します。
[14]で：=
アウト[14] =
その後、Lewから新しいメッセージを受け取りました。三角形6、7、21、および22を少し使用すると、最終的に7つの三角形を1つだけに置き換えることができます。
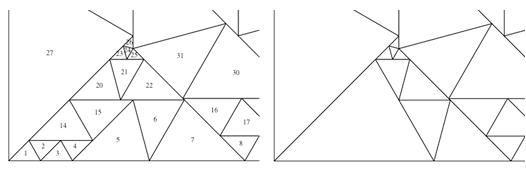
これは非常に単純ではありませんでしたが、正確な頂点座標の新しいセットを見つけました。
[15]で：=
[16]で：=
その結果、50個の三角形を含むソリューションが作成されました。 これは正確な解決策ですか？ 以下のコードを使用して、すべての三角形の角度を計算します。
[17]で：=
[18]で：=
アウト[18] =
各三角形の角度がまったく同じ（45°、60°、75°）であることが簡単にわかるため、バクスターのソリューションは実際には正確です。 50個の三角形を含むソリューションを見てみましょう。
[19]で：=
アウト[19] =
だから私はルー・バクスター150ドルを借りている。 数値最適化の問題に対処したことがあり、正確な解を見つけることが複雑で明確でない場合は、Wolfram言語でRootApproximantなどの関数を使用してみてください。