数年前、私は金と石油価格の関係に関する
興味深い記事に出会いました。
そして、私はモデルを少し拡張し、自分の研究を行うことにしました。
まず第一に、2つの商品ではなく、より実質的なセットを取ります。
インターネットで長時間検索した後、35年間製品の価格アーカイブ(
XLSをダウンロード )をダウンロードした
このサイトを見つけました。
MATLABですべてのデータを処理しました。
xls = xlsread('data.xls');
3つ以上の製品の相対価格として、価格を幾何平均で割った値を使用できます。
geom_average = ones(size(time))';
正規化された価格のチャート:
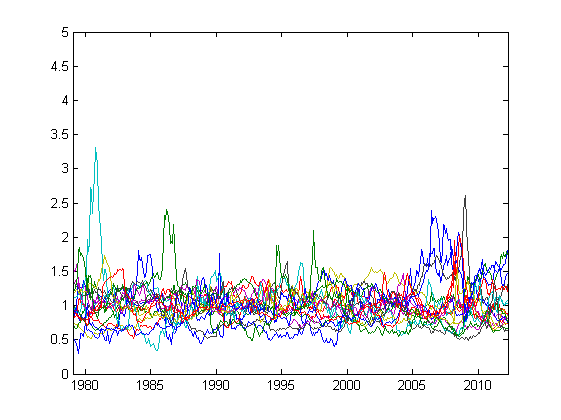
一定期間の平均に対する割合としての相対価格の標準偏差:
| 原油 | 37.77% | ガス | 32.18% | ご飯 | 19.71% |
| ゴールド | 21.57% | お茶 | 25.18% | 綿 | 24.52% |
| ログ | 20.33% | たばこ | 20.55% | 銅 | 36.24% |
| とうもろこし | 15.71% | 小麦 | 14.58% | コーヒー | 37.08% |
| 牛肉 | 19.39% | 砂糖 | 37.91% | 石炭 | 21.68% |
| 鶏肉 | 25.47% | 大豆 | 12.68% | | |
次に、多様化した製品(DP)を作成してみます。
xを商品の相対量のベクトルとし、sum(x
i )= 1;
A-正規化された価格の共分散行列。
次に、多様化された製品の分散がX '* A * Xとして計算されます。
最小化する必要があります。
典型的な条件付き極値問題は、ラグランジュ乗数法によって解決されます。
詳細は説明しませんが、次のように決定されます。
A = cov(all_goods_rel);
DPの構成は次のとおりです。
| 原油 | 0.0035バレル | ガス | 23.2千BTU | ご飯 | 310.3 g |
| ゴールド | 9.627 mg | お茶 | 76.3グラム | 綿 | 98.1 g |
| ログ | 0.353 cc dm | たばこ | 45.69 g | 銅 | 45.79 g |
| とうもろこし | 970.2 g | 小麦 | 514.2 g | コーヒー | 40.7グラム |
| 牛肉 | 64.2 g | 砂糖 | 538.8 g | 石炭 | 3,5 kg |
| 鶏肉 | 148.8グラム | 大豆 | 416.5 g | | |
DPのコストを計算します。
DP = all_goods_rel*x(1:goods_count);
グラフを作成します。

上は相対値のグラフ、下はドル単位の値です。
30年以上にわたるDPの相対値の標準偏差はわずか1.06%です!
しかし、ドルでの価値は増加しています(それぞれ、ドルの購買力は低下しています)。
では、この購買力は何に依存するのでしょうか?
むかしむかし、米国政府の債務に関するデータに出会いました。
ここ (pp。143-144)で、 ここで公的債務に関する詳細なデータを見つけ
、それを
XLSファイルに転送しました。
テーブルからデータを取得します。
debt_xls = xlsread('usa_debt.xls'); debt_time = debt_xls(:,1); end_index = size(debt_time,1); start_index = (1:end_index)*(debt_time == 1978); debt_time = debt_time(start_index:end_index); debt_usd = debt_xls(start_index:end_index,2); debt_percent = debt_xls(start_index:end_index,3); debt_time = debt_time + 1;
そして、グラフを作成してみてください:
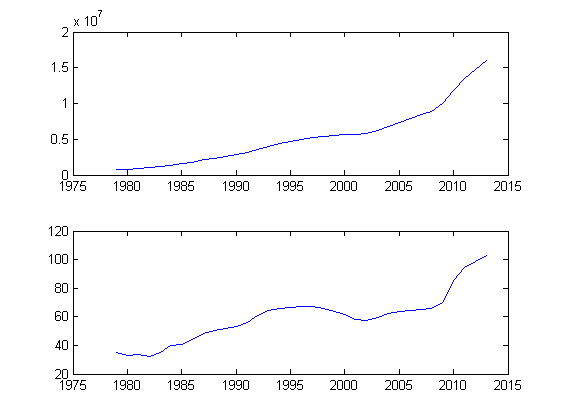
上のグラフは数百万ドル単位の米国政府の負債の量であり、下のグラフはGDPの割合です。
GDPの%での債務の振る舞いと多様化された製品のコストにいくつかの類似点があることに気付くかもしれません。
では、これら2つのグラフを重ねてみてはどうでしょうか。
これを行うには、移動平均を使用してDPのコストを平滑化し、時間間隔全体の負債額を内挿し、時間の経過とともに平均で除算します。
a = 1; b = ones(1,24)/24; debt_interp = interp1(debt_time, debt_percent, real_time, 'cubic')';
次の図が表示されます。
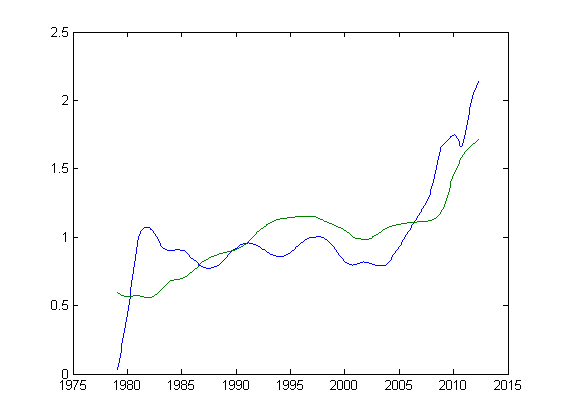
また、ドルでの子会社の価値と負債額の間の相関係数を計算することもできます。これは0.7165または71.65%であり、かなり重要な数字です。
完全なmatlabスクリプトは
、githubで
表示できます(2017年9月9日更新のリンク)。
あとがき
今日の経済はどうですか?
ご存知のように、ほとんどの国際取引は米ドルで行われます。
ルーブルもドルに固定されています。中央銀行は、輸出から受け取ったドルと同数のルーブルを経済に放出し、この金額にドル/ルーブル為替レートを掛けることができます。
何ができますか?
バランスの取れた通貨単位(SDE)の概念を導入し、それを一部の外貨ではなく、多様化された製品に結び付けます。
次のように実装できます。
SDEと外国のVの通貨があると仮定します。
Vに関連するSDE為替レートは、通貨VのDPの値に何らかの係数qを掛けたものとしてインデックス付けされます。
エクスポートおよびインポート操作を検討してください。
1V = 20 SDEとしましょう。
輸出する
オプション1
外部バイヤーは、1000VまたはVで20,000 SDEの量の商品を購入します。
中央銀行で1000Vが「安定」し、20000SDEが経済に放出されます。
オプション2
外部バイヤーが中央銀行から20,000 SDEを受け取り、それらで商品を購入します。
つまり、実際には、将来、同量の商品を返品することを約束します。
インポート。
オプション1
内部バイヤーは、Vで1000Vまたは20000 SDEの量で外部から商品を購入します。
中央銀行は準備金から1000Vを発行し、20,000 SDEが経済から撤退します。
オプション2
内部購入者は、SDEの外部から商品を購入します。
結論:理論上ETSを導入することで、実質的にインフレを回避し、ゼロに近いローンの金利を導入することができます。