ソフトウェアレンダラー-1：マテリアル

ソフトウェアレンダリングは、GPUの助けを借りずに画像を作成するプロセスです。 このプロセスは、2つのモードのいずれかで実行できます。リアルタイム（ゲームなどの対話型アプリケーションでは、1秒あたりの多数のフレームの計算が必要）および「オフライン」モード（1つのフレームの計算に費やすことができる時間）厳密に制限されているわけではありません-計算は数時間または数日続くことがあります）。 リアルタイムレンダリングモードのみを検討します。

このアプローチには、欠点と利点の両方があります。 明らかな欠点はパフォーマンスです-この領域では、CPUは最新のグラフィックスカードと競合できません。 利点には、ビデオカードからの独立性が含まれます。そのため、ビデオカードが1つまたは別の機能をサポートしない場合（いわゆるソフトウェアフォールバック）、ハードウェアレンダリングの代わりとして使用されます。 また、Direct3D 11の一部であるWARPなど、ハードウェアレンダリングをソフトウェアで完全に置き換えることを目的とするプロジェクトもあります。

しかし、主な利点は、そのようなレンダラーを自分で作成できることです。 これは教育目的に役立ち、私の意見では、基礎となるアルゴリズムと原則を理解するための最良の方法です。

これはまさにこれらの記事のシリーズで議論されるものです。 ウィンドウ内のピクセルを指定された色で塗りつぶす機能から開始し、これに基づいて、3Dシーンをリアルタイムでレンダリングする機能、テクスチャモデルと照明の移動、このシーンを移動する機能を構築します。

ただし、少なくとも最初のポリゴンを表示するには、そのポリゴンが構築されている数学を習得する必要があります。 最初の部分は彼女専用であるため、多くの異なるマトリックスと他のジオメトリが含まれます。

記事の最後に、プロジェクトのgithubへのリンクがあります。これは実装の例と考えることができます。

この記事では非常に基本的なことを説明していますが、読者は理解するために特定の基礎が必要です。 この基盤：三角法と幾何学の基礎、デカルト座標系とベクトルの基本操作の理解。 また、ゲーム開発者向けの線形代数の基礎に関する記事（たとえば、 この記事）を読むことをお勧めします。なぜなら、私はいくつかの操作の説明をスキップし、私の観点から最も重要なものだけを取り上げるからです。 なぜいくつかの重要な公式が導き出されるのかを示すつもりですが、それらを詳細に説明するつもりはありません。完全な証明を自分で行うか、関連文献で見つけることができます。 この記事では、まず特定の概念の代数的定義を示し、次にそれらの幾何学的解釈について説明します。 ほとんどの例は2次元空間にあります。3次元空間、特に4次元空間での私の描画スキルには、多くの要望が残されているためです。 それでも、すべての例は他の次元の空間に簡単に一般化できます。 すべての記事は、コードでの実装ではなく、アルゴリズムの説明に焦点を当てます。

ベクトル

ベクトルは、3次元グラフィックスの重要な概念の1つです。 そして、線形代数は非常に抽象的な定義を与えますが、私たちの問題の枠組みでは、 n次元ベクトルによって、 n 個の実数の配列、つまり空間R ^nの要素を意味することができます：



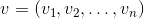
これらの数値の解釈は、コンテキストによって異なります。 最も一般的な2つ：これらの数値は、空間内のポイントの座標または方向変位を指定します。 それらの表示は同じ（ n個の実数）であるという事実にもかかわらず、それらの概念は異なります-ポイントは座標系での位置を表し、変位はそのような位置を持ちません。 将来的には、オフセットを使用してポイントを決定することもできます。これは、オフセットが原点から来ることを意味します。

原則として、ほとんどのゲームおよびグラフィックエンジンには、正確に数値のセットとしてベクトルのクラスがあります。 これらの番号の意味は、使用されるコンテキストによって異なります。 このクラスは、幾何ベクトルの操作（ベクトル積の計算など）およびポイント（2点間の距離の計算など）のメソッドを定義します。

混乱を避けるために、この記事の枠組みの中で、「ベクトル」という単語を数字の抽象的なセットとして理解することはできなくなりますが、それをオフセットと呼びます。

スカラー積

（基本的な性質のために）詳細に説明したいベクトルの操作は、スカラー積のみです。 名前が示すように、この作業の結果はスカラーであり、次の式によって決定されます。



スカラー積には、2つの重要な幾何学的解釈があります。

1. ベクトル間の角度の測定。
   3つのベクトルから得られた次の三角形を考えます。
   
   
   
   彼の余弦定理を書き、式を減らして、次のレコードに到達します。
   
   
   
   非ゼロベクトルの長さは定義により0よりも大きいため、角度のコサインはスカラー積の符号とゼロへの等価性を決定します。 取得します（角度は0〜360度と仮定）：
   
   
   
   
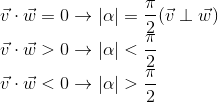
2. スカラー積は、ベクトルのベクトルへの投影の長さを計算します。
   
   
   
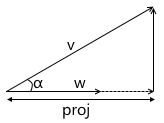
   角度のコサインの定義から次のようになります。
   
   
   
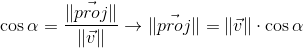
   また、前の段落から次のことをすでに知っています。
   
   
   
   2番目の式から角度の余弦を表現し、最初の式に代入して|| w ||を乗算します 結果が得られます。
   
   
   
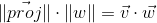
   したがって、2つのベクトルのスカラー積は、ベクトルwにベクトルwの長さを乗算したベクトルvの射影長に等しくなります。 この式の頻繁な特殊なケース-wには単位長があるため、スカラー積は正確な投影長を計算します。
   
   この解釈は、スカラー積が、指定された軸に沿ったポイントの座標（原点からのオフセットを意味するベクトルvによって与えられる）を計算することを示すため、非常に重要です。 最も簡単な例：
   
   
   
   将来的には、カメラ座標系への変換を構築するときにこれを使用します。
   
   

座標系

このセクションは、マトリックスの導入の基礎を準備することを目的としています。 グローバルシステムとローカルシステムの例を使用して、1つではなく複数の座標系が使用される理由と、1つの座標系を別の座標系に対してどのように記述するかについて説明します。

たとえば、2つのモデルでシーンを描く必要があると想像してください。



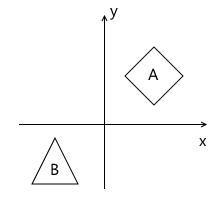
そのような声明から自然に続く座標系は何ですか？ 1つ目は、シーン自体の座標系です（図に示されています）。 これは、描画する世界を記述する座標系です。これが「世界」と呼ばれる理由です（写真では「世界」という単語で示されます）。 彼女は、シーンのすべてのオブジェクトを「結び付け」ます。 たとえば、この座標系におけるオブジェクトAの中心の座標は（1、1）であり、オブジェクトBの中心の座標は（-1、-1）です。

したがって、1つの座標系が既に存在します。 次に、シーンで使用するモデルがどのような形で登場するかを考える必要があります。

簡単にするために、モデルは単純に、それが構成するポイント（「ピーク」）のリストによって記述されると仮定します。 たとえば、モデルBは、次の形式の3つのポイントで構成されています。

v ₀ =（x ₀ 、y ₀ ）
v ₁ =（x ₁ 、y ₁ ）
v ₂ =（x ₂ 、y ₂ ）

一見、必要な「世界」システムで既に説明されているとすばらしいでしょう。 想像してみてください。シーンにモデルを追加すると、すでに必要な場所にあります。 モデルBの場合、次のようになります。

v ₀ =（-1.5、-1.5）
v ₁ =（-1.0、-0.5）
v ₂ =（-0.5、-1.5）

しかし、このアプローチを使用しても機能しません。 これには重要な理由があります。異なるシーンで同じモデルを再び使用することが不可能になるからです。 上の例のように、シーンに追加したときに適切な場所に表示されるようにモデル化されたモデルBが与えられたと想像してください。 その後、突然、需要が変化しました-それを完全に異なる位置に移動したいと思います。 このモデルを作成した人は、自分でモデルを移動し、それをあなたに返さなければならないことがわかります。 もちろん、これはまったくばかげています。 さらに強力な議論は、インタラクティブなアプリケーションの場合、モデルはステージ上で移動、回転、アニメーション化できるということです。それで、アーティストはすべての可能な位置でモデルを実行できますか？ それはさらに愚かに聞こえます。

この問題の解決策は、モデルの「ローカル」座標系です。 オブジェクトの中心（または条件付きで受け入れられるもの）が原点に位置するようにオブジェクトをモデル化します。 次に、オブジェクトのローカル座標系をプログラムでワールドシステムの目的の位置に向けます（移動、回転など）。 上記のシーンに戻ると、オブジェクトA （時計回りに45度回転した単位正方形）は次のようにモデル化できます。



この場合のモデルの説明は次のようになります。

v ₀ =（-0.5、0.5）
v ₁ =（0.5、0.5）
v ₂ =（0.5、-0.5）
v ₃ =（-0.5、-0.5）

そして、それに応じて、2つの座標系-ワールドとローカルオブジェクトAのシーン内の位置：



これは、複数の座標系があることで開発者（およびアーティスト！）の作業が楽になる理由の一例です。 また、別の理由があります-異なる座標系への移行は、必要な計算を単純化できます。

ある座標系と別の座標系の説明

絶対座標のようなものはありません。 何かの記述は常に、ある座標系に関連して起こります。 別の座標系の説明を含む。

上記の例では、座標系の一種の階層を構築できます。

 -ワールドスペース
    -ローカルスペース（オブジェクトA）
    -ローカルスペース（オブジェクトB）

私たちの場合、この階層は非常に単純ですが、実際の状況では、より強力な分岐を持つことができます。 たとえば、オブジェクトのローカル座標系には、身体の特定の部分の位置を担当する子システムがある場合があります。

各子座標系は、次の値を使用して親を基準にして記述できます。

• 親に対する子システムの原点
• 親に対する子システムの基本ベクトルの座標

たとえば、次の図では、 x'y 'システムの原点（ O'と表記）は点（1、1）にあり、その基底ベクトルi 'およびj'の座標は（0.7、-0.7）および（ 0.7、0.7）です。 ） （それぞれ、時計回りに45度回転した軸にほぼ対応）。



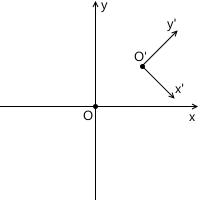
世界座標系は階層のルートであるため、世界座標系を他の座標系について説明する必要はありません。世界座標系の位置や向きは関係ありません。 したがって、それを説明するために、標準ベースを使用します。

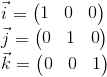
あるシステムから別のシステムへのポイントの座標の変換

親座標系（ P _parentで示される）の点Pの座標は、子システム（ P _childで示される）のこの点の座標と、親に対するこの子システムの方向（座標の原点O _childおよび基底ベクトルi 'を使用して説明されます）およびj ' ）は次のとおりです。



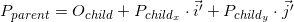
上記のサンプルシーンに戻ります。 世界に対してオブジェクトAのローカル座標系を方向付けました：



既に知っているように、レンダリングのプロセスでは、オブジェクトの頂点の座標をローカル座標系から世界に変換する必要があります。 これを行うには、世界に対するローカル座標系の説明が必要です。 次のようになります：点（1、1）の原点、および基底ベクトルの座標は（0.7、-0.7）および（ 0.7、0.7）です （回転後の基底ベクトルの座標の計算方法については後述しますが、今のところ十分な結果が得られています） 。

たとえば、最初の頂点v =（-0.5、0.5）を取り、ワールドシステムでその座標を計算します。



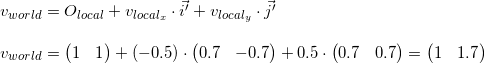
上の画像を見ると、結果の正確性を確認できます。

行列

次元mxnの行列は、対応する数値の表です。 マトリックスの列数が行数と等しい場合、マトリックスは正方と呼ばれます。 たとえば、 3 x 3マトリックスは次のとおりです。

行列乗算

M （次元axb ）とN （次元cxd ）の2つの行列があるとします。 式R = M・Nは 、行列Mの列数が行列Nの行数に等しい場合にのみ定義されます（つまり、 b = c ）。 結果の行列の次元はaxdに等しくなります （つまり、行の数は行の数Mに等しく、列の数はNの列の数になります）、位置ijにある値は、 j番目のMの i番目の行のスカラー積として計算されます列N ：



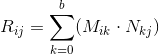
2つの行列M・Nの乗算の結果が定義されている場合、逆方向の乗算も決定されることを意味するわけではありません-N・M （行と列の数は一致しない場合があります）。 一般的な場合、行列乗算の演算も可換ではありません： M・N≠N・M

単位行列とは、別の行列に乗算された行列（つまり、 M・I = M ）を変更しない行列です。通常の数値の単位の一種です。

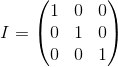
行列ベクトル

ベクトルを行列として表すこともできます。 これを行うには、「行ベクトル」と「列ベクトル」と呼ばれる2つの方法があります。 名前が示すとおり、行ベクトルは1行の行列として表されるベクトルであり、列ベクトルは1列の行列として表されるベクトルです。

文字列ベクトル：



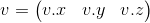
列ベクトル：



さらに、非常に頻繁にベクトル（次のセクションで説明します）でマトリックスを乗算する操作に遭遇し、先を見据えて、作業するマトリックスは3 x 3または4 x 4の次元を持ちます。

3次元ベクトルに3 x 3行列を乗算する方法を検討します（他の次元にも同様の考慮事項が適用されます）。 定義により、最初の行列の列数が2番目の行列の行数と等しい場合、2つの行列を乗算できます。 したがって、 1 x 3行列（行ベクトル）と3 x 1行列（列ベクトル）の両方としてベクトルを表現できるため、2つの可能なオプションがあります。

• 行列「左」によるベクトルの乗算：
  
  
  
  
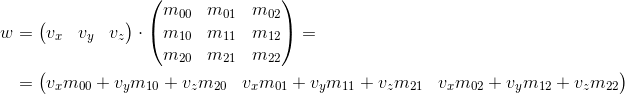
• 行列「右」によるベクトルの乗算：
  
  

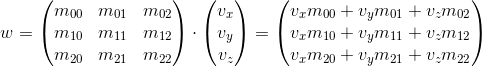
ご覧のとおり、各ケースで異なる結果が得られます。 これにより、APIで両側でマトリックスをベクトルで乗算できる場合、ランダムエラーが発生する可能性があります。これは、後で説明するように、変換マトリックスはベクトルに2つの方法のいずれかで乗算されることを意味するためです だから、私の意見では、APIでは2つのオプションのうちの1つだけに固執する方が良いです。 これらの記事のフレームワークでは、最初のオプションを使用します-つまり ベクトルは左側の行列で乗算されます。 別の順序を使用する場合は、正しい結果を得るために、この記事で後述するすべての行列を転置し、「行」という単語を「列」に置き換える必要があります。 これは、いくつかの変換が存在する場合の行列乗算の順序にも影響します（詳細については後述します）。

また、乗算結果から、特定の方法で（要素の値に応じて）マトリックスが乗算されたベクトルを変更することがわかります。 回転、スケーリングなどの変換が可能です。

行列乗算演算のもう1つの非常に重要な特性は、将来的に私たちにとって有用になると思われますが、加算に関する分配性です。

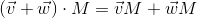
幾何学的解釈

前のセクションで見たように、マトリックスはベクトルに乗算されたベクトルを特定の方法で変換します。

任意のベクトルは基底ベクトルの線形結合として表すことができることをもう一度思い出してください。





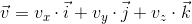
この式に行列を乗算します。



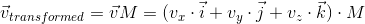
加算に関する分配性を使用して、以下を取得します。



子システムから親システムにポイントの座標を変換する方法を検討したときに、これをすでに見ましたが、次のようになりました（3次元空間の場合）：



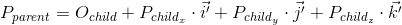
2つの式には2つの違いがあります-最初の式には動きがありません（ O _child 、線形およびアフィン変換について説明するときにこの瞬間をより詳細に検討します）、ベクトルi ' 、 j'およびk 'は iM 、 jMおよびそれぞれkM 。 したがって、 iM 、 jM 、およびkMは子座標系の基本ベクトルであり、点v _child （v _x 、v _y 、v _y ）をこの子座標系から親（ v _transform = v _parent M ）に_変換します。

反時計回りの回転の例では、変換プロセスを次のように表すことができます（ xyは元の親座標系、 x'y 'は変換の結果の娘です）。



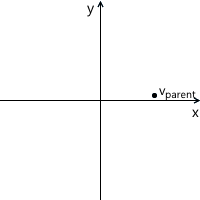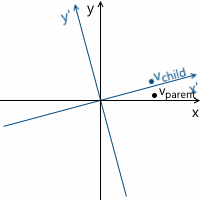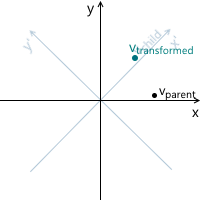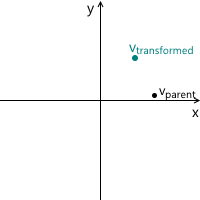
念のため、上記で使用した各ベクトルの意味を確実に理解できるように、それらを再度リストします。

• v _parentは、元々行列Mで乗算したベクトルです。 その座標は、親座標系を基準にして記述されます。
• v _childは、その座標がベクトルv _parentに等しいベクトルですが、それらは子座標系に関連して記述されます。 これは、基本ベクトルと同じ方法で変換されたベクトルv _親です （同じ座標を使用するため）
• _変換されたvは、 v _childと同じベクトルですが、座標は親座標系を基準にして再カウントされます。 これは、ベクトルv _親を変換した最終結果です

ここで、基底ベクトルに行列Mを掛けるとどうなるかを考えてみましょう。





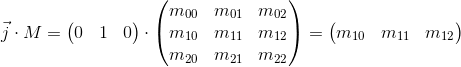
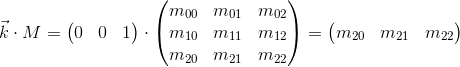
行列Mを乗算して得られた新しい娘座標系の基底ベクトルは、行列の行と一致することがわかります。 これは私たちが探していた非常に幾何学的な解釈です。さて、変換行列を見たところで、それが何をしているのかを理解するためにどこを見るべきかを知ることができます-その座標系を新しい座標系の基底ベクトルとして想像してください。座標系で行われる変換は、ベクトルにこの行列を掛けて行われる変換と同じです。

また、マトリックス形式で表される変換を互いに乗算することで結合することもできます。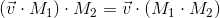



したがって、マトリックスは、変換を記述および結合するための非常に便利なツールです。

線形変換

最初に、最も一般的に使用される線形変換を検討します。線形変換-満たす二つの特性こと変換：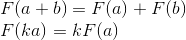



重要な結果は-線形変換が移動することを含むことができない（これはまた、長期的理由であるOの_子、以降、第二式によれば、前のセクションには存在しない）は0常にで表示される0。

回転

2次元空間での回転を考慮してください。これは、座標系を特定の角度だけ回転させる変換です。すでにわかっているように、新しい座標軸（特定の角度で回転した後に得られる）を計算し、それらを変換行列の行として使用するだけで十分です。結果は、基本的なジオメトリから簡単に取得できます。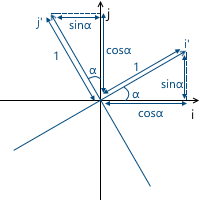





例：



3次元空間での回転の結果も同様に取得されますが、2つの座標軸で構成される平面を回転し、3番目の座標軸（回転が発生する周辺）を固定する点のみが異なります。たとえば、x軸の周りの回転行列は次のとおりです。

スケーリング

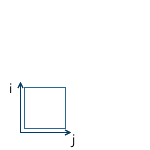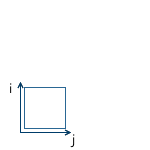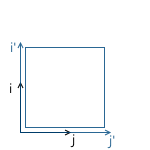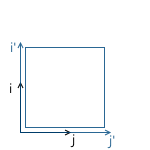
次のマトリックスを適用することにより、すべての軸に対するオブジェクトのスケールを変更できます。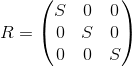



変換された座標系の軸は、元の座標系と同じ方法で方向付けられますが、1測定単位に対してS倍の時間が必要になります。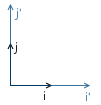



例：


すべての軸に関して同じ係数でスケーリングすることを均一と呼びます。しかし、異なる軸に沿って異なる係数でスケーリングすることもできます（不均一）。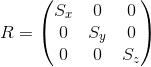

シフト

名前が示すように、この変換は座標軸に沿ってシフトを生成し、残りの軸はそのまま残します。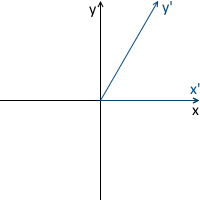



したがって、y軸のシフトマトリックスは次のようになります。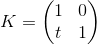



例：



3次元空間のマトリックスも同様の方法で作成されます。たとえば、x軸をシフトするオプション：



この変換はめったに使用されませんが、アフィン変換を検討するときに将来便利になります。

在庫にはすでにかなりの数の変換があり、3 x 3マトリックスとして表すことができますが、もう1つ不足しています-変位。残念ながら、変位は線形変換ではないため、3 x 3行列を使用して3次元空間で変位を表現することはできません。この問題の解決策は同種の座標です。これについては後で検討します。

中央投影

最終的な目標は、2次元のスクリーンに3次元のシーンを描くことです。したがって、何らかの方法で平面上でシーンを設計する必要があります。最も一般的に使用される投影法には、正射投影法と中央投影法（別名-遠近法）の2種類があります。

人間の目が3次元のシーンを見ると、人間が見る最終画像では、それから遠く離れたオブジェクトが小さくなります。この効果は遠近法と呼ばれます。正投影は、遠近法を無視します。これは、さまざまなCADシステム（および2Dゲーム）で作業する場合に便利なプロパティです。中央投影にはこの特性があるため、リアリズムのかなりの部分が追加されます。この記事では、彼女だけを検討します。

正射投影とは異なり、遠近投影の線は互いに平行ではなく、投影の中心と呼ばれる点で交差します。投影中心は、シーンを見る「目」であり、仮想カメラです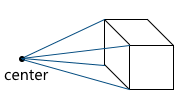



。画像は、仮想カメラから所定の距離にある平面上に形成されます。したがって、カメラからの距離が大きいほど、投影サイズは大きくなります。



最も単純な例を考えてみましょう。カメラは原点にあり、投影面はカメラから距離dにあります。投影したいポイントの座標がわかっています：（x、y、z）。平面上のこの点_の投影の座標x _pを見つけます。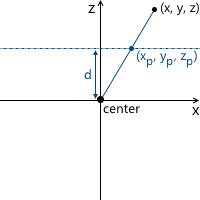



この図では、2つの類似した三角形が表示されています-CDPおよびCBA（3つの角度で）：



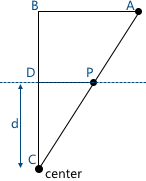それぞれ、側面間の関係が保持されます：x座標



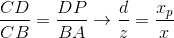の結果を取得します：同様に、y座標の場合：この変換を使用して形成する必要があります投影画像。そして、ここで問題が発生します- マトリックスを使用した3次元空間でのz座標への分割は想像できません。変位行列の場合のように、この問題の解決策は同次座標です。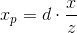

射影幾何と同次座標

これまでに、2つの問題が発生しました。

• 3 x 3

これらの問題は両方とも、均一な座標を使用することで解決されます。同種座標-射影幾何学からの概念。射影幾何学は射影空間を研究し、同次座標の幾何学的解釈を理解するには、それらを知る必要があります。

以下では、2次元射影空間の定義を検討します。これは、2次元射影空間の方が描写しやすいためです。同様の考慮事項が3次元射影空間に適用されます（将来的に使用します）。

空間R ³の光線を次のように定義します。光線はkv形式のベクトルのセットです（kはスカラー、vは非ゼロのベクトル、空間R ^3の要素）。つまりベクトルvは光線の方向を定義します：



これで射影空間の定義に進むことができます。射影平面（すなわち、次元を持つ射影空間が2に等しい）P ²空間に関連付けられたR ^3は、で複数のビームであるR ³。したがって、P ^2の「ポイント」はR ^3の光線です。

したがって、中の2つのベクトルR ³セットの一方とに同じ要素P ²（この場合、それらは1つの光線上にあるため）、それらの一方がスカラに秒を乗じて得られることができれば。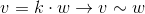



たとえば、ベクトル（ 1、1、1 ）と（5、5、5）は同じ光線を表します。つまり、これらは射影平面の同じ「ポイント」です。

したがって、我々は均一な座標になりました。射影平面の各要素は、3つの座標（x、y、w）の光線で定義されます（最後の座標は、zの代わりにwと呼ばれる-一般に受け入れられている合意）-これらの座標は同種と呼ばれ、スカラーまで決定されます。これは、スカラーの同次座標で乗算（または除算）できることを意味します。これらの座標は、射影平面内の同じ「ポイント」を表します。

将来的には、同種の座標を使用して、アフィン（動きを含む）変換と投影を表します。しかし、その前にもう1つの問題を解決する必要があります。与えられたモデル頂点を同次座標の形でどのように提示するのでしょうか。同次座標への「加算」は3番目の座標wの加算により発生するため、問題は、wのどの値を使用する必要があるかということになります。この質問に対する答えはゼロ以外です。wの異なる値を使用する際の違いは、それらを操作する便利さです。



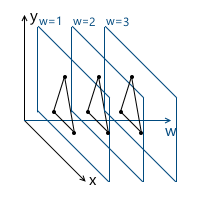そして、さらに理解されるように（そして、それは部分的に直感的に明確です）、wの最も便利な値は1です。この選択の利点は次のとおりです。

• ( )
• ( ) w , (.. w):
  
  
  
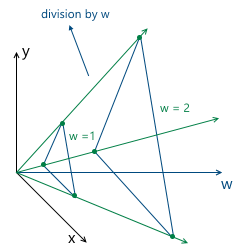
  — w = 1 , w — , w

したがって、値w = 1を選択します。これは、同次座標の入力データが次のようになることを意味します（もちろん、ユニットは既に追加されており、モデルの説明自体には含まれません）

。v ₀ =（x ₀、y ₀、1）、
V ₁ =（X ₁、Y ₁ 1）
V ₂ =（X ₂、Y ₂、1）

を操作するとき今では特別な場合を考慮する必要があるwの座標です。つまり、ゼロに等しい。wの任意の値を選択できると上記で述べました、ゼロではなく、同次座標に展開します。特に、w = 0を取ることはできません。なぜなら、この点を移動できないためです（後で説明するように、w座標の値によって移動が正確に行われるため）。また、点wの座標がゼロの場合、「無限」にある点と見なすことができます。なぜなら、平面w = 1に戻ろうとすると、ゼロによる除算が得られるからです。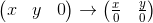



また、モデルの頂点にnull値を使用することはできませんが、ベクトルにはnull値を使用できます！これは、ベクトルが位置を記述しないため、変換中にベクトルが変位の影響を受けないという事実につながります。たとえば、法線を変換する場合、それを移動することはできません。そうしないと、間違った結果が得られます。ベクトルの変換が必要になった場合、これをより詳細に検討します。

これに関して、w = 1の場合は点を記述し、w = 0の場合はベクトルを記述するとよく書かれています。

すでに書いたように、2次元の射影空間の例を使用しましたが、実際には3次元の射影空間を使用します。つまり、各ポイントは4つの座標で記述されます：（x、y、z、w） 。

均一な座標を使用して移動する

これで、アフィニティ変換を記述するために必要なツールがすべて揃いました。アテナイ変換-その後の変位を伴う線形変換。4 x 4行列を使用して、同次座標を使用したアフィン変換を記述



することもできます：同次座標として表されるベクトルを乗算し、4 x 4行列を乗算した結果を考えます：ご覧のように、変換との違い3 x 3行列の形式で表される4番目の座標と、v _w・m _3i形式の各座標の新しい項で構成されます。これを使用して、w = 1を意味します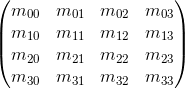









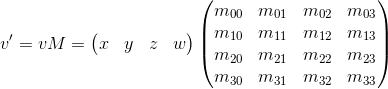
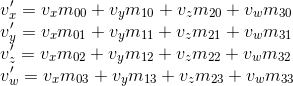、変位を次のように表すことができます：



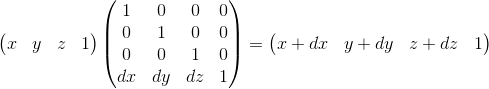ここで、w = 1の正しい選択を検証できます。変位dxを表すには、形式w・dx / wの項を使用します。したがって、行列の最後の行は（dx / w、dy / w、dz / w、1）のようになります。w = 1の場合、分母を単純に省略できます。

このマトリックスには、幾何学的な解釈もあります。前に調べたシフト行列を思い出してください。形式はまったく同じです。唯一の違いは、4番目の軸がシフトされることです。したがって、超平面w = 1にある3次元部分空間が対応する値だけシフトされます。

仮想カメラの説明

仮想カメラは、シーンを見る「目」です。先に進む前に、空間内のカメラの位置をどのように記述できるか、および最終画像の形成に必要なパラメーターを理解する必要があります。

カメラパラメーターは、切り捨てられたビューのピラミッド（視錐台）を指定します。これにより、シーンのどの部分が最終画像に分類されるかが決まり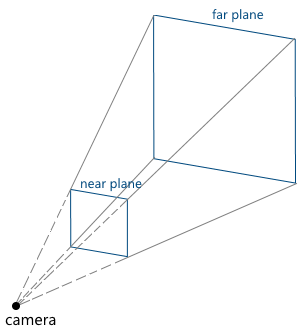



ます。

• . , , . . «UVN» , .. . , u , v n ( ), right , up forward — , . .
  
  
  
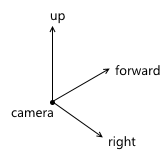
  API — . , , up ( up' ). :
  
  
  • right forward up' :
    
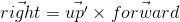
  • up , right forward :
    
  
  , up' forward , up . OpenGL, gluLookAt .
  
  — ,
  
  
• z-カメラ座標系のニアおよびファークリッピングプレーン（ニア/ファークリッピングプレーン）の座標
  
  
• カメラアングル。 レビューの切り捨てられたピラミッドのサイズを指定します。
  
  
  
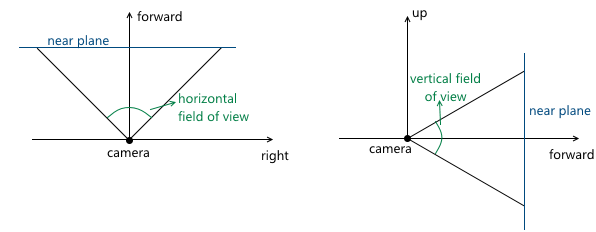
  シーンは投影面に投影されるため、この平面の画像はコンピューターの画面に表示されます。 したがって、この平面と画像が表示されるウィンドウ（またはその一部）のアスペクト比が一致することが重要です。 これは、APIユーザーに1つの表示角度のみを指定し、ウィンドウのアスペクト比に従って2番目の表示角度を計算する機能を提供することで実現できます。 たとえば、水平方向の視野角がわかっている場合、次のように垂直方向を計算できます。
  
  
  
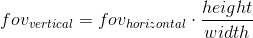
  中央投影について説明したとき、投影面がカメラから遠くなるほど、結果の画像のサイズが大きくなることがわかりました。カメラから（原点にあると仮定して） z軸に沿った変数dの投影面までの距離を示します。 したがって、 dの値を選択する必要があるという問題を解決する必要があります。 実際、ゼロ以外の値。 dの増加とともに画像サイズが増加するという事実にもかかわらず、ビューのピラミッドと交差する投影面の部分は比例して増加し、平面のこの部分の寸法に対して同じ画像スケールを残します。 将来的には、便宜上d = 1を使用します。
  
  2Dの例：
  
  
  
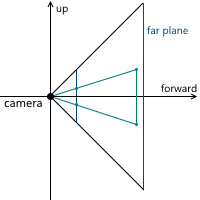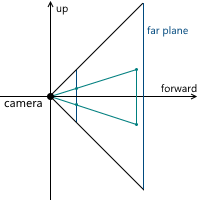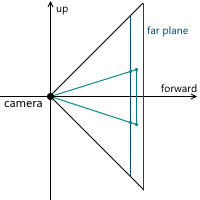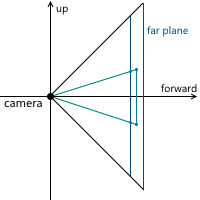
  その結果、画像の縮尺を変更するには、視野角を変更する必要があります。これにより、投影ピラミッドと交差する投影面の部分のサイズが変更され、投影サイズは同じままになります。
  

カメラを移動および回転して、その座標系の位置と方向を変更できます。 コード例：

グラフィックコンベア

これで、コンピューター画面上の3次元シーンの画像を取得するために必要なステップをステップで説明するために必要なすべての基礎ができました。 簡単にするために、パイプラインは一度に1つのオブジェクトを描画すると仮定します。

インバウンドパイプラインパラメーター：

• 世界座標系でのオブジェクトとその向き
• 画像をコンパイルするときにパラメータを使用するカメラ

1.世界座標系への移行

この段階で、オブジェクトの頂点をローカル座標系から世界に変換します。

世界座標系でのオブジェクトの方向は、次のパラメーターによって定義されると仮定します。

• ワールド座標系のどの点にオブジェクトがあるのか​​： （x _world 、y _world 、z _world ）
• オブジェクトの回転方法： （r _x 、r _y 、r _z ）
• オブジェクトスケール： （s _x 、s _y 、s _z ）

これらの変換の行列をそれぞれT 、 R、およびSと呼びます。 オブジェクトを世界座標系に変換する最終的なマトリックスを取得するには、それらを乗算するだけで十分です。 ここで、行列の乗算の順序が役割を果たすことに注意することが重要です。これは、行列の乗算が非可換であるという事実から直接生じます。

スケーリングは原点を基準にして発生することを思い出してください。 最初にオブジェクトを目的のポイントに移動してからスケールを適用すると、間違った結果が得られます。スケーリング後にオブジェクトの位置が再び変更されます。 簡単な例：



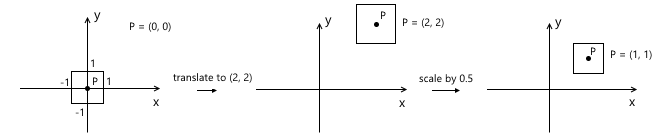
同様の規則が回転に適用されます-原点を基準にして発生します。つまり、最初に移動するとオブジェクトの位置が変わります。

したがって、この場合の正しいシーケンスは次のとおりです。スケーリング-回転-変位：

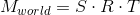
2.カメラ座標系への移行

特に、カメラ座標系への移行は、さらなる計算を簡素化するために使用されます。 この座標系では、カメラは原点に配置され、その軸は前のセクションで調べたforward 、 right 、 upのベクトルです 。

カメラ座標系への移行は、2つのステップで構成されます。

• カメラの位置が原点と一致するように世界を移動します
• 計算された軸right 、 up 、 forwardを使用して、これらの軸に沿ったオブジェクトの頂点の座標を計算します（この手順は、カメラの座標系を回転させてワールド座標系と一致させることと見なすことができます）

最初のステップは、 （-pos _x 、-pos _y 、-pos _z ）上の変位行列として簡単に表すことができます。ここで、 posは世界座標系のカメラ位置です。



2番目のポイントを実装するには、最初に検討したスカラー積のプロパティを使用します。スカラー積は、指定された軸に沿った投影の長さを計算します。 したがって、ポイントAをカメラの座標系に変換するには（カメラが原点にあるという事実を考慮して、最初の段落でこれを行いました）、ベクターのスカラー積、 up 、 forwardを取得するだけです。 世界座標系vの点と、カメラの座標系v 'に変換された同じ点を示します：



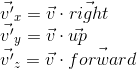
この操作は、マトリックスとして表すことができます。



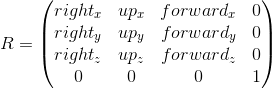
これらの2つの変換を組み合わせて、カメラ座標系の遷移行列を取得します。



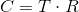
概略的に、このプロセスは次のように表すことができます。

3.均一なクリッピングスペースへの移行と座標の正規化

前の段落の結果として、カメラ座標系でオブジェクトの頂点の座標を取得しました。 次に行うことは、これらの頂点を平面に投影し、余分な頂点を「切り取る」ことです。 オブジェクトが表示ピラミッドの外側にある場合、オブジェクトの上部は切り取られます（つまり、その投影は、表示ピラミッドが覆う平面の一部にありません）。 たとえば、次の図の頂点v ₁ ：



これらのタスクは両方とも、射影行列によって部分的に解決されます。 「部分的に」-投影自体は生成されませんが、このために頂点のw座標を準備するためです。 このため、「投影行列」という名前はあまりふさわしくありませんが（これはかなり一般的な用語ですが）、切り捨てられた表示ピラミッドを均質なクリッピングスペース（均質な）クリップスペース）。

しかし、まず最初に。 そのため、最初は投影の準備です。 これを行うには、頂点のz座標をw座標に配置します。 投影自体（つまり、 zによる除算）は、w座標をさらに正規化すると発生します。 空間w = 1に戻るとき。

このマトリックスが次に行うべきことは、オブジェクトの頂点の座標をカメラ空間から同種のクリップ空間に変換することです。 これは、投影を適用した後（つまり、古いz座標を保存したためw座標で除算した後）、頂点の座標が正規化されるように、切り捨てられていない頂点の座標である空間です。 次の条件を満たす。



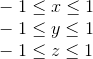z座標の不等式は、APIによって異なる場合があります。 たとえば、OpenGLでは、上位のものに対応します。 Direct3Dでは、 z座標は間隔[0、1]で表示されます。 OpenGLで受け入れられる間隔、つまり [-1、1] 。
このような座標は、正規化デバイス座標（または単にNDC）と呼ばれます。

座標をwで除算することによりNDC座標を取得するため、クリッピング空間の頂点は次の条件を満たします。



したがって、頂点をこの空間に変換することにより、上の不等式の座標をチェックするだけで頂点を切り取る必要があるかどうかを知ることができます。 これらの条件を満たさない頂点はすべてカットオフする必要があります。 正しい実装は新しい頂点の作成につながるため、クリッピング自体は別の記事のトピックです。 これまでのところ、簡単な解決策として、頂点の少なくとも1つが切り取られている場合は顔を描画しません。 もちろん、結果はあまり正確ではありません。 たとえば、マシンモデルの場合、次のようになります。



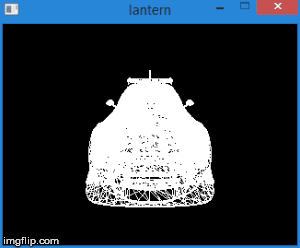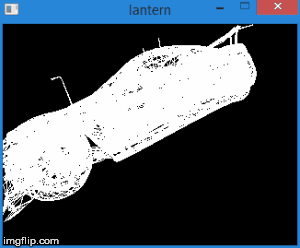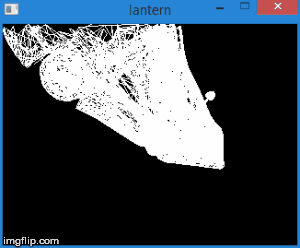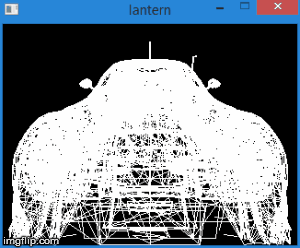
全体として、この段階は次の手順で構成されます。

• カメラ空間の頂点を取得します
• カットオフマトリックスを乗算-カットオフスペースに移動
• 上記の不等式でチェックして、カットオフ頂点をマークします
• 各頂点の座標をそのw-座標で除算-正規化された座標に移動

次に、カメラ空間からクリッピング空間に座標をマッピングする方法を検討します。 投影平面z = 1を使用することにしたことを思い出してください。 最初に、区間[-1、1]のビューのピラミッドと投影面の交点にある座標を表示する関数を見つける必要があります。 これを行うには、平面のこの部分を定義する点の座標を見つけます。 これらの2つのポイントには、座標（左、上）と（右、下）があります。 ビューのピラミッドがカメラの方向に対して対称である場合のみを考慮します。



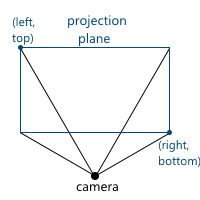
表示角度を使用してそれらを計算できます。



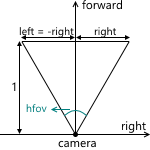
取得するもの：



同様にtopとbottomについても ：



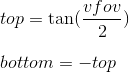
したがって、間隔[left、right] 、 [bottom、top] 、 [near、far]を[-1;にマッピングする必要があります。 1] 。 左と右にそのような結果を与える線形関数を見つけます：



同様に、 bottomとtopの関数を取得します：



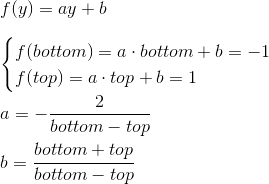zの式は異なります。 形式az + bの関数を考慮する代わりに、関数a・1 / z + bを考慮します。これは、将来、深度バッファを実装するときに、z座標の逆数を線形補間する必要があるためです。 今はこの問題を考慮せず、当然のことと考えています。 取得するもの：



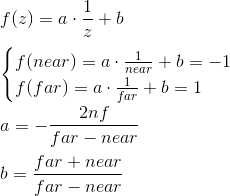
したがって、正規化された座標は、カメラ空間の座標から次のように取得されると書くことができます。



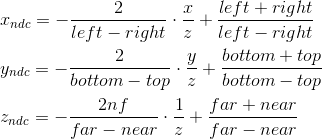zによる除算は後で行われ、 w座標が正規化されるため、これらの式をすぐに適用することはできません。 これを利用して、代わりに次の値を計算し（zで乗算）、 wで除算した後、正規化された座標になります。



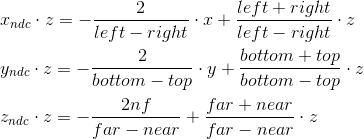
これらの式を使用して、カットオフスペースに変換しています。 この変換を行列形式で書くことができます（さらにzをw座標に入れたことを思い出してください）：

スクリーン座標系に移動

現在の段階では、NDCのオブジェクトの頂点の座標があります。 それらをスクリーン座標系に変換する必要があります。 投影面の左上隅が（-1、1）にマッピングされ、右下隅が（1、-1）にマッピングされたことを思い出してください。 画面では、座標系の原点として左上隅を使用し、軸は右下を指します。



このビューポート変換は、単純な式を使用して実行できます。



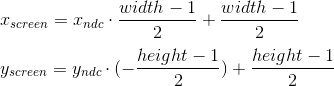
または、マトリックス形式で：



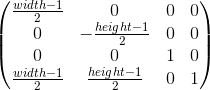
デプスバッファを実装するためにz _ndcの使用はそのままにします。

その結果、画面上の頂点の座標が得られ、これを使用して描画します。

コード実装

上記の方法を使用してパイプラインを実装し、ワイヤフレームモードでレンダリングを実行する（つまり、頂点を線で単純に接続する）コードの例を次に示します。 また、オブジェクトは、頂点のセットと、そのポリゴンが構成する頂点（面）のインデックスのセットによって記述されることを意味します。

SDL2の実装例

このセクションでは、SDL2を使用してレンダリングを実装する方法について簡単に説明します。

初期化、テクスチャ作成

最初の方法は、もちろん、ライブラリの初期化とウィンドウの作成です。 SDLからグラフィックのみが必要な場合は、 SDL_INIT_VIDEOフラグで初期化できます。

次に、描画するテクスチャを作成します。 ARGB8888形式を使用します。これは、テクスチャの各ピクセルに4バイトが割り当てられることを意味します。RGBチャンネルに3バイト、アルファチャンネルに1バイトです。

アプリケーションの終了時にSDLとそこから取得したすべての変数を「クリア」することを忘れないでください。

描画、画面に表示

SDL_UpdateTextureを使用してテクスチャを更新し、それを画面に表示できます。 この関数は、とりわけ、次のパラメーターを受け入れます。

• データはバイトの配列で、対応する値を持つピクセルの配列です
• 画像の1行のバイト数（ピッチ）は、ピクセル数に4を掛けた値として計算されます（形式がARGB8888であるため）

描画機能をバイトの配列で表されるテクスチャに分離し、別のクラスにすることは論理的です。 配列にメモリを割り当て、テクスチャをクリアし、ピクセルとラインを描画します。 ピクセル描画は次のように実行できます（バイト順はSDL_BYTEORDERによって異なります ）

線の描画は、たとえばBresenhamアルゴリズムに従って実装できます。

SDL_UpdateTextureを使用した後、テクスチャをSDL_Rendererにコピーし、 SDL_RenderPresentを使用して表示する必要があります。 すべて一緒に：

以上です。 プロジェクトへのリンク： https : //github.com/loreglean/lantern