バーチ・スウィナートン・ダイアー予想

この注目すべき仮説は、定義されているかどうかが現在不明である関数Lの動作と、有限であるかどうかが不明なグループIIIの順序を結び付けます！
JTTate、楕円曲線の算術、発明数学23（1974）

（40年前の引用の関連性についての簡単なリファレンス：Wiles and Co.の後、関数Lは複素平面全体で決定できることがわかった。一般的な場合のグループIIIの有限性は不明のままである。）

エラーの可能性については議論する必要があります。 内部コンピューターエラーに対する予防措置として、すべての計算を2回実行するか、プログラム内でチェックを行うことができます。 さらに、コンピューターは、人間とは異なり、エラーが大きすぎて見過ごされないように設計されています。 結果にそのようなエラーがないことを確信しています。 一方、複雑な計算スキームをコンピュータープログラムにコーディングする場合、プログラミングエラーは避けられません。 それらのほとんどは、プログラムがハングするか、とんでもない結果をもたらすため、メインの起動前でも検出されます。 しかし、動作していると見なされるプログラムには、まれな状況で発生する論理エラーが依然として含まれている可能性があります。実際、ほとんどのコンピューターは異常の影響を受けやすいため、仕様に従って動作するはずの動作と異なる場合があります。 実際、ステップ（ii）のプログラムは不正確であることが判明し、見つけなければならない非常に少数の同等物を見逃しました。

これらの理由により、コンピューターで得られた結果を自動的に信頼すべきではないと考えています。 場合によっては、本質的に計算に関与しておらず、起こりうるエラーを乗り切る可能性が低いプロパティを犠牲にしてチェックできます。 （たとえば、補間なしで得られた滑らかな関数の値の表は、隣接する値の差を計算することで確認できます）。しかし、そのようなチェックが利用できない場合、別のコンピューター上の別のプログラマーによって独立して確認されるまで、結果を完全に信頼するべきではありません。 コンピュータが非常に広く利用可能になったときに、これが過度の基準を設定するとは思わない。 そして、低水準がすでに公表され、誤った結果を信じていることを確信しています。

BJBirchおよびHPFSwinnerton-Dyer、楕円曲線に関する注意。 I、Journalfürdie reine und angewandte Mathematik 212（1963）

猫の下では、仮説の定式化はありません。 「オイラー積」や「ホロモルフィック継続」などの知識のある表現（言語の観点と指定された概念の観点）は、Clay InstituteのWebサイトから5ページのPDFを読むことができます。 カットの下では、一般的な数学的思考の発展がバーチ-スウィナートン-ダイアー仮説である方向を説明する試みがいくつかあります。 また、KDPVに表示されているような大きな数字を1秒未満でカウントする方法。

2つの変数を持つ方程式の合理的な解を見つけることです。

線形および二次方程式

最も単純なケースは線形方程式です： a x + b y + c = 0（ここでa 、 b 、 cは有理数です）。 ここでの解決策は簡単です。a= b = 0の縮退したケースを除外すると、変数の1つは任意の合理的な値を取ることができ、もう1つは最初から一意に計算されます。

次のケースは二次方程式です。 すでにさまざまなケースがありますが、すべてが明確なケース（ y -x²= 0、 y² -x²= 0）を横切ると、残りの変数は線形変化によりa x²+ b y² + cの形に減少します = 0、ここで 、 a 、 b 、 cは非ゼロの有理数です。 3つの特徴的な例を見てみましょう。

明らかに、最初の例には合理的な解がありません。なぜなら、左側は常に1以上であり、ゼロに等しくできないからです。 別の言い方をすれば、最初の例には実際の解すらなく、有理数は実数のサブセットであるため、合理的な解もありません。

2番目の例に合理的な解決策がないことはそれほど明白ではありません。 xとyを最小公分母にします。x = k / n 、 y = m / nとします。ここで、 k 、 m 、 nは整数であり、集合体では相互に単純です（つまり、3つすべてを同時に分割する数はありません） 。 その後、方程式はに変換されます 。
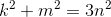
3を法とすると考えてください。3を法とする整数の2乗は0または1のいずれかです。 3を法とする2つの2乗和は、両方の数値が3で割り切れる場合にのみゼロになります。したがって、 kとmは3で割り切れる必要があります。
次に、モジュール9 =3²を取得します。 左側は9で割り切れるので、3 n²は9で割り切れる必要があり、 nは3で割り切れる必要があります。したがって、 k 、 m 、 nは整数で相互に単純で、元の方程式には有理解がありません。そして約束された。


3番目の方程式には、簡単に示すためのソリューションがいくつかあります。たとえば、 x = 1、 y = 0です。 二次方程式の1つの解がわかっている場合、ディオファントスに遡る方法ですべてを見つけることは難しくありません：点（1,0）を通る直線は正確に他の1つの点で円と交差し、この点は角が直接係数は合理的です。 特に円の場合、角度係数を-tで表すと、直線の形式はy =（1- x ） tになり、円との2番目の交点x²+ y² = 1の座標は
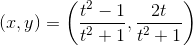
-これは、3番目の例の一般的な解決策です（ポイント（1,0）自体を除く、これはある意味で ）

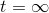
ハッセの原理

整数または有理数の係数を含む方程式に同じ数のべき乗を与えるという考え方は、非常に有益です。 特別な構造「 p 、p²、および他のすべての次数pを法として起こることだけに関心があり、他の算術プロパティを無視するとしましょう」は、「 p進数 」と呼ばれます （Wikipediaへのリンクがあります。しかし、時にはひどい言葉がそこに出くわします）; 実数のようなp進数は有理数を含み、他の多くを追加します（たとえば、2の平方根はモジュロ7と7のすべての次数で抽出されるため、7進数の中にあります;一方、 4を法としても3を法としても抽出できないため、2進および3進の数には含まれません）。 2番目の例に関する引数は、文字通り3進の数値に引き継がれます。2番目の例には3進の解はなく、有理数は3進のサブセットであるため、合理的な解もありません。
多くの場合、1つの素数での作業は簡単で楽しいものです。 最終的に、素数を法とするすべてのオプションを整理することができます。 一方、複数の素数を扱うことははるかに複雑になる傾向があります- ゴールドバッハ 問題と双子問題はこのことの明確な証拠です。

実数とp進数に渡すと、解決策がないことを証明するのに役立ちます。 逆に、ハッセの原理では、すべてのpに対して実数解とp進解がある場合、必然的に合理的な解が存在するということです。 （もちろん、無限に多くの素数があり、すべてのテストが遅延する可能性があります。しかし、 pが分子、分母a 、 b 、 c 、および2以上を分割しない場合、常にp進解があり、除数abc二次相反の法則を使用して解の存在を効果的に検証します。）

残念ながら、ハッセの原理は、より高次の方程式には当てはまりません。 たとえば、方程式3 x ³ +4 y ³ + 5 = 0にはすべてのpに対して実数解とp進解があるが、合理的な解がないことが証明できます。

楕円曲線

y （x²-1）= x ³ -1やy² = x ³ + x²のような異なる縮退した場合をもう一度除けば、3次の方程式は、属1の曲線を定義します（これは定義ではなく、属の他の曲線があります1）。 曲線上に点がない場合があります（方程式の解）。 点があり、それらのいずれかが選択されている場合、 楕円曲線が取得されます。 楕円曲線の場合、選択したポイントを無限に送信するために変数をいつでも変更でき、標準形式y² = x ³ + a x + b 、 a 、 b有理式（および整数でさえ、変数の別の変更によって分母をいつでも取り除くことができます）の方程式を取得できます楕円曲線（有理数以上）のみが次に来るでしょう。

非公式に言えば、正確にハッセの原理が単一の楕円曲線と関連するエンティティに対してどのように違反されるかは、テート-シャファレヴィッチ曲線のグループによって特徴付けられ、テートのプレゼンテーションは伝統的にキリル文字IIIでほとんどの文字が英語の記事でも示されています。 それは有限であると仮定されます。 Birch-Swinnerton-Dyer仮説には、このグループの順序が含まれます。

二次方程式とは異なり、1つの点を見つけて（そして無限に送信した後）、すべてが始まります。 楕円曲線上の点を追加できることはよく知られています。 1つのポイントを取得し、それを自分自身に追加し始めると（ P 、 P + P = 2 P 、 P + P + P = 3 P 、...）、2つのオプションが可能です：特定のステップ数の後、無限にリモートになります（その後、次のステップで再びPが与えられ、プロセスがループします）、または結果のすべてのポイントが異なります（そして-P 、 -2Pなども取るのが理にかなっています）。 最初の場合、この点はねじれ点と呼ばれます。 単一の曲線の場合、11を除く1から12までが可能です（常に存在する無限遠点はねじれ点でもあります）。 Mordell – Weilの定理は、曲線上の任意の点がn ₁ P ₁ + ... + nの形式で一意に記述されるように、常に有限数（おそらく0）の第2タイプの点P ₁ 、...、 P _rを見つけることができると述べています。 _r P _r + Q 、ここでQはねじれ点、 n _iは整数です。 数値rは、曲線のランクと呼ばれます。 たとえば、KDPVに描かれた曲線y² = x ³ +877 xには、ランク1と2つのねじれ点があります。 曲線の（合理的な）点は、 n Pまたはn P +（0,0）のいずれかです。ここで、 P座標は図で署名されています。

すべてのねじれ点を見つけるのは比較的簡単です。 たとえば、整数係数aおよびbの場合、すべてのねじれ点（無限遠のものを除く）自体は整数座標を持ち、 y座標はゼロまたはy²が4 a ³ +27 b²を除算します。 ランクの計算およびポイントP _iを生成するための検索_は、はるかに複雑です。

何かを理解する時です

単純にx座標の分子と分母を昇順に調べ、有理yが得られるかどうかをチェックすることにより、曲線上の点を検索できます。 曲線の整数係数の場合、分母xは正確な正方形であり、分母yは同じ数の立方体である必要があります（KDPVの分母は78841535860683900210の2乗および立方体です）。 ただし、KDPV曲線は、それを見ると芽のような考えが抑制されるように特別に選択されます（ Pは（0,0）をカウントせず、最小の分母を持つ点です）。

原則として、 n- descent（ nは2以上の正の整数）の一般的な手順があります。これにより、Tate-Shafarevichグループにn次の要素がなく、 rの上限と下限を取得して、 rを計算し、 r 個の独立点を見つけることができます。一般的なケースでいくつかの独立点を見つけます。 （後者の場合、下降を繰り返すことができます。nとして、ある素数の次数の増加を選択します。Tate-Shafarevichグループが有限の場合、有限時間後に収束します。）しかし、実際には、それは非常に不便です。 BirchとSwinnerton-Dyerは、2つの記事の最初の記事で、実際の算術の範囲を超えない2降下法を提案しました。 正確な説明が必要な場合は、 mwrankのソース、 特にmwrank1.ccを調べて 、 y² = x ³ +877 xの結果をいくつか示します。

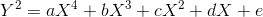
最初の段階で、メソッドは四次曲線-フォームの曲線を検索します 、-元の曲線へのマッピングがあり、特定の範囲でa 、 b 、 cをソートし 、 dとeを計算し、 dとeが整数であることを確認し、実点またはp進点を持たない四次数を削除します少なくともいくつかのp 。
最初の段階の後、いくつかの四分数が同等になることがあります（ Xの線形の分数変化によって互いに通過します）。 2番目の段階では、メソッドは各等価クラスから1つの四次を残します。 この後、2 ^{m + k} -1 4次が残ります。初期曲線上に次数2の0.1.3ポイント（ y = 0で特徴付けられる）がある場合、係数2 ^kは1.2または4です。mはランク。 曲線y² = x ³ + 877 xには、次数2のポイントが1つあり、ランクは1であるため、3つの四次数が取得されます。

最初のもの：





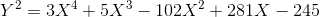
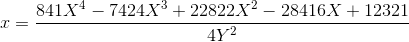
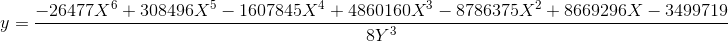
（Habr形式は、すべての係数の式を書き出すことを好みませんが、それでも座標変換のすべての係数はa 、 b 、 c 、 d 、 eを介して計算されます。たとえば、12321はd²-8e c / 3として取得されます。 ）



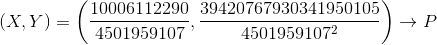
第二：






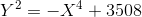
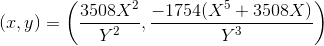
第三：





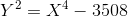
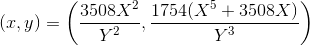
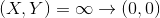
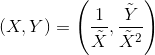
（ aが正確な正方形であるかどうかに応じて、0または2つの無限遠点が4次に存在する可能性があります。最初の2つの4次には、 2つあり、両方とも（0,0）になります。 それらを通常のポイントに減らします。）

3番目の段階で、このメソッドは、2番目の段階の後に残っている4次数の合理的なポイントを検索します。 元の曲線のx-座標の分子と分母は、四次の分子のX-座標の4番目の次数にほぼ等しくなります（楕円曲線のnを乗算すると、 n²の演算になり、2次元の場合は次数4になります）。 ポイントが見つかった場合、それを使用して、元の曲線上のポイントを計算できます。 ポイントが見つからなかった場合、問題が発生します。これは、ポイントが実際に存在しない（およびTate-Shafarevichグループの重要な要素がある）か、検索が不十分だったことを意味します。 理論的な解決策は、高次の降下を同時に開始し、大きな分子と分母を持つポイントを検索することです。 良い実用的な解決策は不明です。

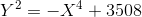
曲線y² = x ³ + 877 xの場合、四次曲線上の座標は元の曲線の点の座標よりも印象的ではありませんが、直接列挙するには大きすぎます。 ただし、四次の さらに下がることができます。 （最初の4次をさらに処理することは困難ですが、必要ではありません。1つの生成点で十分です。）右側は2次であり、つまりX²で表されます。 これは、初期曲線に2次ポイントがある場合に常に発生します（ y = 0の場合）。 ペア（X²、 Y ）を変数として使用すると、2次方程式が得られますが、これは既に解くことができます。

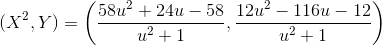
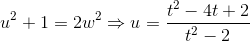
さらに、X²の式の分子と分母の公約数も除算する必要があります ; それらの商は、両方とも " d ×square"の形式の場合にのみ商になります。ここで、 dは平方なしの除数3508です。つまり、数字1,2,877,1754の1つです（分母は常に正であるため、負のdは除外されます）。 分子は、2進（特に有理数）数の正確な二乗にはできません。 d = 2を試します。 。 得られたuの式を分子に代入し、分子が二重の正方形であることを要求すると、新しい四次式が得られます 。
すでに列挙に利用できるポイントがあります： 。

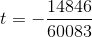
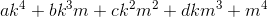
四分位数の検索は、プライムとプライムの累乗を法とする方程式を考慮するという同じ考え方を使用してさらに削減できます。 整数k 、 mを検索するとき、 正確な二乗で、各素数pに対して、p²可能な残基のペア（ k 、 m ）の約半分は、 pを法とする非平方を与えます。 （2と3の代わりに、それらの次数16と9を見る方が良いです。大きなpの場合 、次数を増やしても何も与えられません。）したがって、例えば16 * 9 * 5 * 7の剰余のペアは合計の約1/16です可能なペアの数。 「良い」残基を持つペア（ k 、 m ）のみを検索するだけで十分です。 前述のmwrankは、同様の考慮事項を使用して、FDPCを持つポイントPを1秒未満で見つけます。

バーチ・スウィナートン・ダイアー予想

最初の記事、楕円曲線に関する注意。 バーチとスウィナートン・ダイアーは、数千の楕円曲線のランクに関する統計を収集しました。 2番目の記事「楕円曲線に関する注意。 II」、蓄積された統計を分析する時が来ました。タイトル仮説もそこで提案されています。

有理数の楕円曲線を使用すると、問題が発生する場合があります。点の座標が急速に増加するため、ランクを計算する手順で常に答えが得られるとは限りません。 一方、整数係数の方程式がある場合、異なる素数を法としてそれを考慮することができます。 小さな素数を法とする点の数は直接計算するのは簡単ですが、その数が合理的な点とどのような関係にあるかは明確ではありません。

各素数について、この素数を法とする曲線上の点の数を数えると、整数の無限集合が得られます。 このセットを特定の方法で複素変数の単一の関数に「接着」 すると 、伝統的に文字Lで示される楕円曲線のハッセ-ワイルゼータ関数が得られます。 一度にすべての素数を法とする動作に関する情報が含まれているため、それについて何かを証明することは困難です。 （この点では、リーマンゼータ関数に似ています。リーマンゼータ関数の特性に関するリーマン仮説は、「ミレニアム問題」のもう1つです。）ランク）ゼータ関数のプロパティを使用し、有限モジュールに関する曲線の動作によってのみ計算されます。