こんにちは、Habr。 そしてまさにその通りです。
チャレンジ:
LとRの 2つの整数があります。 区間[L;でA xor Bの最大値を見つける必要があります。 R] 、ここでL≤A≤B≤R。複雑なことは何もないように思えます。 すぐに解決策は単純なバストを頼みます。
展開するpublic int BruteForce(int one, int two) { int maxXor = 0; while (one < two) { int oneTemp = one + 1; while (oneTemp <= two) { int curXor = one ^ oneTemp; if (maxXor < curXor) maxXor = curXor; oneTemp++; } one++; } return maxXor; }
このソリューションの複雑さはO(n
2 )です。
しかし、間隔内に1,000,000個の数字がある場合はどうでしょう。 L = 1、R = 1000001を取ります。平均的なコンピューターがこの間隔で最大xor値を計算するのにどれくらい時間がかかりますか? 私のラップトップは1699914ミリ秒かかりました。
はるかに高速に動作するソリューションがあり、この記事で説明します。

主なアイデア。
結果の数を最大にするためには、この数の可能な限り高いビットで関数xorから1つを取得する必要があります。 など、最年少に向かって。 つまり、結果の数値の各ビットを最上位ビットから最下位ビットの方向に順番に処理します。 このためには、
トライツリーと呼ばれるデータ構造を使用すると非常に便利
です (
このデータ構造については、R。Sagevik著「Java Algorithms」による本での説明が気に入っています )。
トライツリーは、リンクを含むノード(nullまたは他のノードへのリンク)で構成されるデータ構造です。 他の1つのノードのみが各ノードを指します(ノードはルートノードを指しません)。 各ノードにはR個のリンクが含まれます。Rはアルファベットのサイズです(この場合、アルファベットは0と1であるため、R = 2)。 原則として、トライツリーにはかなりの数のヌルリンクが含まれているため、写真からは除外されます。 各リンクは、番号の次のビットに対応しています。 各整数は、ルートからリーフへのパスとしてエンコードされます。
空のトライツリーの例。

これは、0、1、2、3、4、5、6、7を追加した後のトライツリーの外観です。
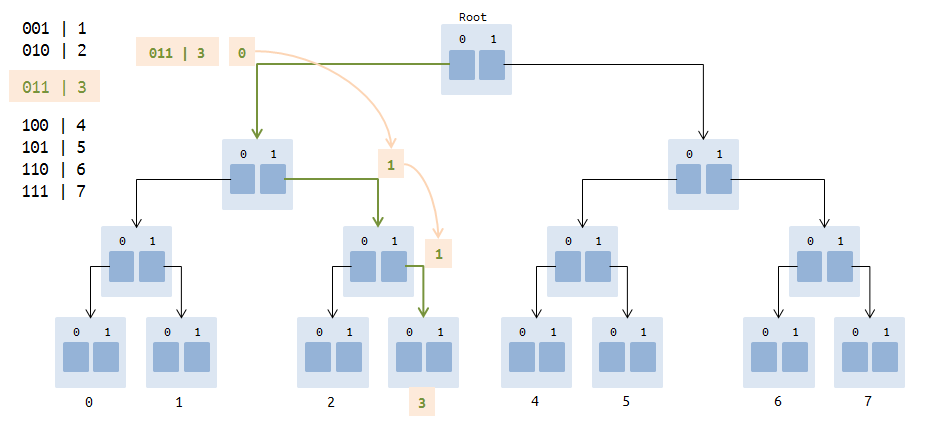
この図は、3つのリンクで構成されるパスを示しています-0-
> 1-> 1 (011は数字3のバイナリ表現です)。
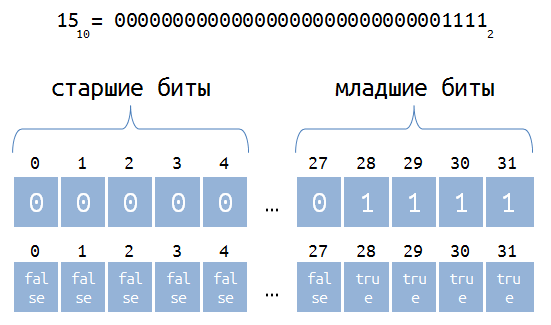
32ビットの数値のみを使用し、必要に応じて最上位ビットにゼロを埋めることをすぐに明確にします。 これにより、数値が同じ長さの配列に格納されるようになります。 整数のバイナリ表現をbool型の配列に保存することにしました。
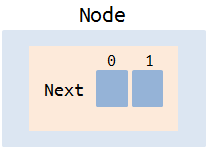
各ノードには、ツリーの他のノードへのリンクの配列が格納されます(2つのリンク、数値のビットの可能な値ごとに1つ)。
一般に、トライツリーは、検索を制御するために検索キーの文字を使用できる文字列キー文字から構築されたデータ構造です。 文字列キーの長さは異なる可能性があるため、ツリーの各ノードは値をさらに格納します。値は、文字列キーの1つに関連付けられたゼロまたは実際の値です。 この場合、キーは同じ長さの配列にバイナリ形式で格納された32ビット整数であるため、値を格納する必要はありません。 だからトライツリー:
using System; namespace MaxXor { public class Trie {
まず、数値を10進数から2進数に、またはその逆に変換する機能が必要です。 ここではすべてが非常に明確でシンプルです。 メモリを更新する必要がある場合は、のぞき見することができます。
ConvertDecimalToBInary private bool[] ConvertDecimalToBInary(int number) { int counter = Trie.MaxLengthOfBits; bool[] result = new bool[counter]; while (number > 0) { result[--counter] = Convert.ToBoolean(number % 2); number /= 2; } return result; }
ConvertBinaryToDecimal private int ConvertBinaryToDecimal(bool[] bits) { int result = 0; int base_val = 1; for (int i = bits.Length - 1; i >= 0; i--) { result += Convert.ToInt32(bits[i]) * base_val; base_val *= 2; } return result; }
次に、整数をトライツリーに追加する関数が必要です。 ここでさらに詳しく説明します。 トライツリーに挿入するには、まず目的のノードを検索する必要があります。 検索はルートから始まり、番号のゼロ(最上位)ビットに関連付けられたリンクをたどります。 このノードから、番号の最初のビットに関連付けられたリンクをたどります。 そこから-番号の2番目のビットに関連付けられたリンクによって。 など。つまり、ルートからトライツリーのノードまでのパスに沿ってノードを調べるだけです。 数値ビットは、最後のビットまたはヌル参照に到達するまでツリーを下降するために使用されます。 数値の最後のビットを取得する前にnull参照が検出された場合、つまり トライツリーでは、番号の最後のビットに対応するノードはないため、欠落しているビットごとにノードを作成する必要があります。
public void AddValue(bool[] binaryNumber) { _root = AddValue(_root, binaryNumber, 0); } private Node AddValue(Node node, bool[] val, int d) { if (node == null) node = new Node();
次に、指定された間隔のすべての数値を追加して、トライツリーを構築します。
更新:
freopenが最初に
正しく気づいたよう
に 、
異なる最初のビットを見つけるだけで十分です。上のビットでは何もできません。下のビットはユニットを作るのが簡単です
したがって、異なる最初のビットを見つけます。このため、両方のリンクを持つノードに到達するまで、ルートに沿ってリンクに沿って移動します。 次に、すべてのビットを単位以下にします。 その結果、結果が得られます。
public bool[] GetMaxXor() { bool[] result = new bool[Trie.MaxLengthOfBits]; Node cur = _root;
コードの大幅な簡素化、ただし複雑さは変わりません! プロジェクトの更新されたソリューションを含むアーカイブは、
ここからダウンロードでき
ます 。
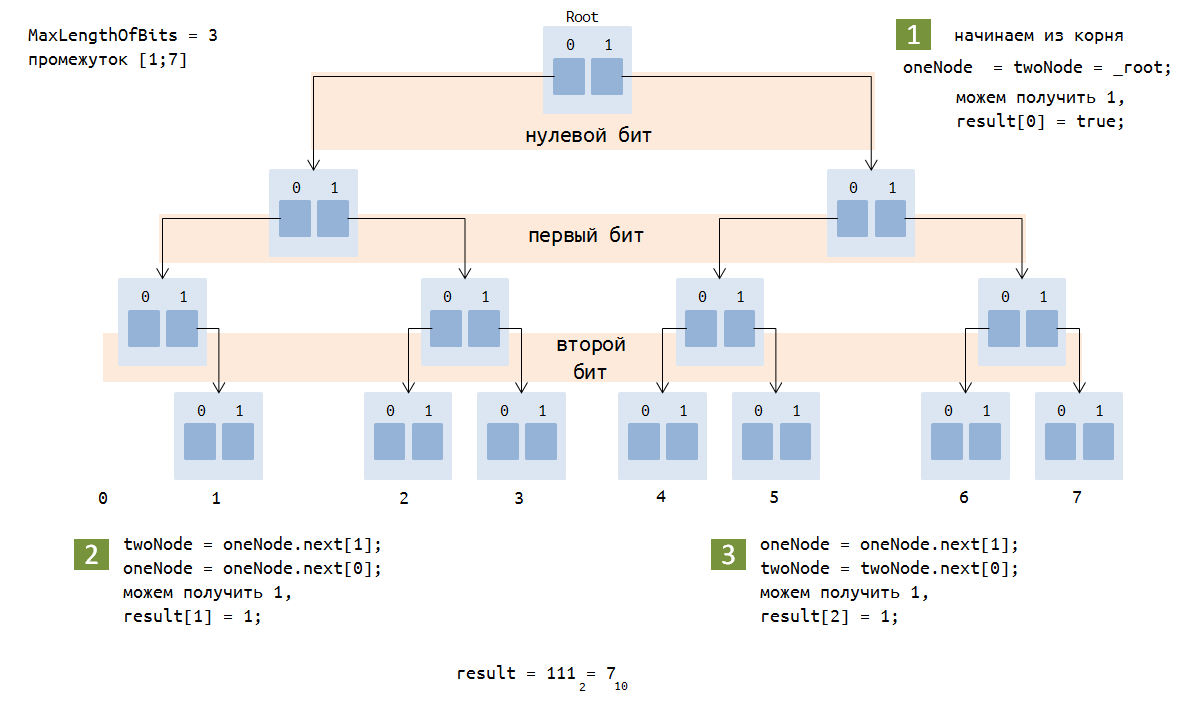
古いバージョン最も重要なことに移ります。 xorの最大値を見つけるために、ルートからトライツリー内のリンクに沿って移動します。つまり、高から低の方向にビットを操作します。 そして、1つのノードと別のノードの両方に配置できます。 各パスで、可能であれば、次のビットのビットのxorからユニットを取得しようとし、32ビットすべてを取得するまで続けます。 結果の32ビット-これは、インターバルの最大xor値です。
public bool[] GetMaxXor() { bool[] result = new bool[Trie.MaxLengthOfBits]; Node oneNode = _root, twoNode = _root;
3ビット数の例
プロジェクトのソリューションを含むアーカイブは
ここからダウンロードでき
ます 。
これで、さまざまな長さのギャップに対する各アプローチの動作時間を比較できます。
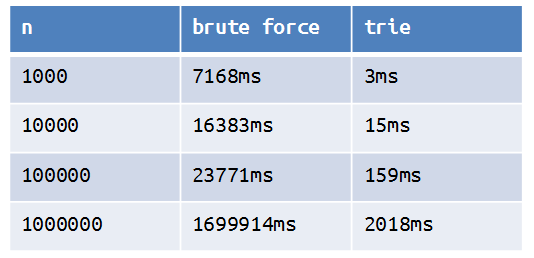
表からわかるように、トライツリーを使用した最大xor値の計算ははるかに高速です。 O(nlogn)アルゴリズムの複雑さの推定。
PSこの問題を解決し、実際にバイナリ形式で整数を保存するために、トライツリーをわずかに単純化できます。 アルファベットは2文字のみで構成されているため、配列を削除して、たとえば
Node leftと
Node rightのように、それぞれ0と1の表現である2つのリンクを保存することができます。