🏫 🦖 🤟🏿 データ構造：2-3ヒープ（2-3ヒープ） 🙈 ⛺️ 💯

いくつかのデータ構造を持つ優先度キューを実装する効果的な方法の問題は、長い間関連したままです。この質問に対する答えは、データを保存するために必要なメモリの量とキュー操作が機能する時間との間の常に妥協のようなものです。

コンピュータサイエンスでは、優先度キューを効率的に実装するためにヒープ構造が使用されます。

ヒープは、ヒーププロパティを満たす特殊なツリー型データ構造です。BがAの子孫ノードである場合、キー（ A ）≥キー（ B ）。したがって、最大のキーを持つ要素は常にヒープのルートノードであるため、そのようなヒープは最大ヒープと呼ばれることもあります（あるいは、比較が行われる場合、最小要素は常にルートノードになり、そのようなヒープは最小ヒープと呼ばれます）。実際には各ヒープノードの数は通常2つ以下ですが、各ヒープノードが持つ子孫ノードの数に制限はありません。ヒープは、ダイクストラのアルゴリズムやピラミッドのソートなど、いくつかの効率的なグラフアルゴリズムで重要です。

優先度キューを格納および操作するための最もよく研究され確立されたデータ構造の1つは、バイナリヒープとフィボナッチヒープです。しかし、これらの構造にはいくつかの特徴があります。

たとえば、基本操作のバイナリヒープの複雑さはΘ（logn）ですが、最小値を見つけることと、そのようなヒープをマージするには線形時間（！）が必要です。しかし、そのようなヒープを保存するには、他のヒープに比べてメモリはほとんど必要ありません。

フィボナッチヒープは、ノードをヒープから削除するときにバランスが取れるため、基本的な操作の複雑さが軽減されます。多数の連続したフィボナッチ加算演算では、ヒープの幅が拡大し、最小値を削除する操作中にのみバランスが発生するため、最小値を取得する操作にはかなりの時間が必要になる場合があります。

高岡忠雄はこの問題の解決策を取り上げ、1999年に「2-3ヒープ」という作品を発表しました ...

「2-3ヒープ」の構造について少し

2-3ヒープ（2-3ヒープ）は、ヒーププロパティ（最小ヒープ、最大ヒープ）を満たすツリー型のデータ構造です。フィボナッチヒープの代替です。 2〜3本の木で構成されています。

2-3ヒープが提供するソリューションは、フィボナッチヒープとは異なり、2-3ヒープは削除時だけでなく、新しい要素を追加するときにもバランスを取り、ヒープから最小ノードを抽出する際の計算負荷を軽減します。

任意のツリーTの頂点tの子の数はこの頂点の次数と呼ばれ、そのルートの次数はツリーの次数と呼ばれます。

2-3ツリーは、誘導的に定義されたツリーT ₀ 、T ₁ 、T ₂ 、...です。ツリーT ₀は単一の頂点で構成されています。ツリーT _iは、2つのツリーT _i-1または3つのツリーで構成されるツリーを意味します。この場合、各後続のルートは、前のルートの右端の子になります。

ツリー2〜3のヒープは、ツリーH [ i ]と呼ばれます。ツリーH [ i ]は、空の2-3ツリー、またはツリーT _iと同様に接続された次数iの 1つまたは2つの2-3ツリーのいずれかです。

2-3ヒープはツリーの配列H [ i ]（ i = 0..n）であり、それぞれのヒーププロパティが満たされています。

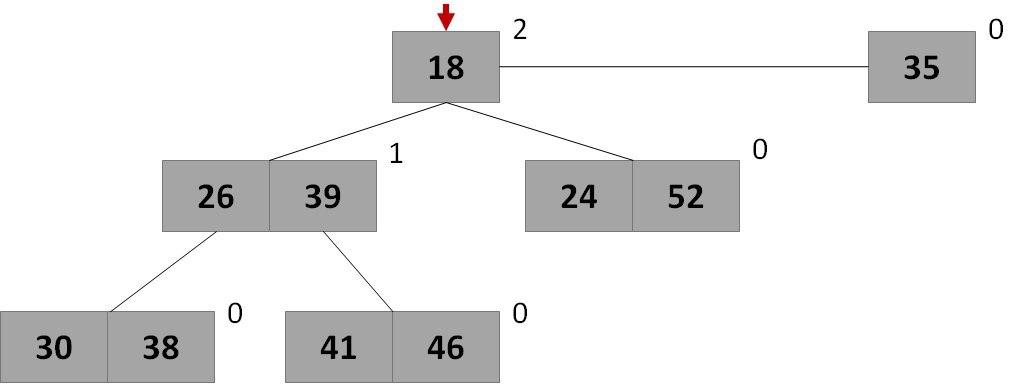図 ヒープの視覚的表現

ノード構造

各ノードには、他のノード（矢印のあるフィールド）、サービスフィールド、およびキー（優先順位）のペア（値）へのポインターがあります。

基本操作

2-3ヒープで最小値を見つける（FindMin）

最小のヒープ要素は、いずれかのヒープツリーのルートにあります。最小ノードを見つけるには、ツリーを歩く必要があります。

ヒープ内の最小ノードへのポインターを維持することにより、一定時間でこのノードを見つけることができます（Θ（1））

2-3ヒープに挿入（挿入）

新しい要素を追加するには、1つの頂点を含むツリーH [0]を作成します
このツリーをヒープに追加する操作を実行しましょう。次数iのツリーをヒープに追加する場合、次のオプションが可能です。
1. この優先順位を持つツリーがない場合は、ヒープに追加してください。
2. そうでない場合は、ヒープからそのようなツリーを抽出し、追加するツリーに接続します。その後、結果のツリーをヒープに追加します
追加した後、ポインターを最小ルートに修正します

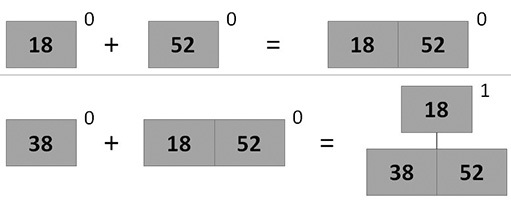
図 2〜3のパイルに順次アイテムを追加するアニメーション

ヒープから最小アイテムを削除する

最小ヒープ要素は、ヒープツリーの1つのルートにあります。たとえば、H [ i ]で-FindMinを使用して検索します。ヒープからツリーH [ i ]を抽出し、そのルートを削除すると、ツリーはサブツリーに分解されます。サブツリーは後でヒープに追加します。

ルートを再帰的に削除します。ツリーが1つの頂点で構成されている場合は、単純に削除します。そうでない場合は、右端の子のルートから切断し、削除を続行します。

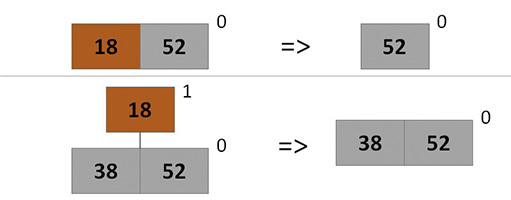
アイテムのキーを減らす

まず、必要なノードでキーを自由に削減できます。この後、確認する必要があります：ノードがツリーのルートにある場合は、他に何もする必要はありません。そうでない場合は、すべてのサブツリーでこのノードを削除し、ヒープに挿入する必要があります（キーは既に変更されています）。

2つのヒープを1つにまとめる

1つに結合する必要がある2つのヒープがあります。これを行うには、2番目のヒープから2〜3個のツリーをすべて抽出し、それらを最初のヒープに挿入します。その後、ノード数のカウンターを修正する必要があります。最初と2番目のヒープに要素数を追加し、最初のヒープのカウンターに結果を書き込み、2番目のヒープにカウンターを0に設定します。

操作の複雑さと他のアルゴリズムの比較

この表は、キュー操作の複雑さを優先度とともに示しています（最悪の場合、最悪の場合）
記号「*」は、トランザクションの償却後の複雑さを示します

運営	バイナリヒープ	二項ヒープ	フィボナッチヒープ	2-3ヒープ
フィンドミン	Θ（1）	O（ログ）	Θ（1）*	Θ（1）*
デリミン	Θ（logn）	Θ（logn）	O（logn）*	O（logn）*
挿入	Θ（logn）	O（ログ）	Θ（1）*	Θ（1）*
減少キー	Θ（logn）	Θ（logn）	Θ（1）*	Θ（1）*
マージ/ユニオン	Θ（n）	Ω（logn）	Θ（1）	Θ（1）*

ご清聴ありがとうございました！

著者の記事2-3 Heapに基づくC ++での実装のソースコードは、 GitHubのMITで入手できます。

PS：このトピックに関するコースプロジェクトを書くとき、RuNetにはほとんど情報がないことに気付いたので、この問題に自分の数セントを追加して、このアルゴリズムについて関心のあるコミュニティに伝えました。

データ構造：2-3ヒープ（2-3ヒープ）