チューリングAマシンとHoarピットストップコーヒーマシン

理論を知らずに練習に頼る人は、舵とコンパスなしで船に乗り込む舵取りのようなものです。
レオナルド・ダ・ヴィンチ

聖なる言語戦争では、言語は同等である限りチューリング完全であるため、最終的な議論がしばしば引用されます。 カットの下で、すでにPythonを習得しており、現在ErlangまたはHaskellを仕様で研究する予定の人のために、この論文を明確にする試み。 素材はパノラマであり、写真で整然としています。

Alan Turingは1936年にa-carを製造しました。

「...エンドレステープは、シンボルでマークされたプラットフォームに分割されます。各瞬間に、マシンで使用できるシンボルは1つだけです。マシンの状態は、使用可能なシンボルによって異なります。マシンはこのシンボルを自由に変更できます。 、それは車の基本操作です。したがって、どのシンボルにもチャンスがあります... "

1948年のエッセイ、インテリジェント機械チューリング。

ステートマシンはマシン内に隠されていると言えるので、開業医にとっては理解しやすいでしょう。
a-machineを組み立てることができるデザイナーは、チューリングが完了したと見なされます。 2つのマシンがチューリングで同等と見なされるのは、一方が他方をパーツか​​ら組み立てることができる場合です。
チューリングは、任意のa-machineを置き換えることができる汎用ユニットをプロトタイプ化しました。 ユニバーサルチューリングマシンは、ある種のプライベートa-machineの説明をデータとともにテープから読み取ることでこれを実現します。 2つのUMTは明らかに同等です。 そして1946年、フォンノイマンがこのプロトタイプを作成しました。 ここで、複雑な計算では、UMTがプライベートa-machineよりも対数的に遅いことに注意してください。
チューリングと教会の仮定：自然数の任意の関数は、万能チューリング機械がそれを処理する場合にのみ、紙と鉛筆を装備した人によって計算可能です。
前述のことから、ユニバーサルチューリングマシンほど急なものはないということがわかります。 システムが何であれ、UMTは引き続き機能します（教会とチューリングの論文が正しい場合）。 それでも、チューリングは彼の車にブレーキがかかっていないことを認めざるを得なかった。 ゲーデルの不完全性定理は、シャットダウンの問題を引き起こします。 UMTが常に停止状態に到達することを確認することはできません。
UMTでの計算は、テープおよび状態遷移に沿った一連のステップです。
たとえば、アセンブラの整数モジュールabs（int）は次のように取ることができます

cdq ;        eax  edx ; if eax>=0 then edx:=0 else edx:=0xFFFFFFFF xor eax, edx ;   XOR  ,      A ⊕ 0 = A ; XOR c -1   NOT A ⊕ –1 = ¬A ; if eax>=0 then eax:=eax xor 0=eax else eax:=eax xor 0xFFFFFFFF=not eax sub eax, edx ;    edx  eax ;  eax , edx=0      ;   eax    1   -eax ; ¬A + 1 = –A ; if eax>=0 then eax:=eax xor 0 - 0=eax else eax:=(eax xor -1) - (-1=not eax + 1= -eax 

Universal Turing Machineを実装するifおよびgotoを備えた命令型プログラミング言語。

同じ1936年に、アロンゾ教会は、その用語に関する3つの簡単な規則で記述されたラムダ計算の世界を導入しました。 （一般に、教会の研究は1928-1930年にさかのぼり、チューリングは教会の大学院生でしたが、彼の作品は同時に出版されました。）
•変数x、y、z ...は用語です（アルファベット）
•MとNが用語の場合、（MN）は用語です（アプリケーション）
•xが変数で、Mが項の場合、（λx.M）は項です（抽象化）
まあ、他のすべてがラムダ用語ではないことも指定されています。
ここでの抽象化は、関数を記述する方法です。 アプリケーション-引数に適用する機能。 ラムダ式はツリーで完全に表現できます。

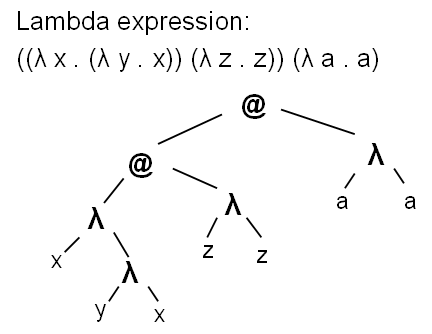
これらの矛盾しない規則の意味を復活させるために、ラムダ式の3種類の縮小（単純化）が導入されています。

• α変換：引数の名前を変更（アルファ）; λx.x→λy.y
• β-reduction：関数を引数に適用（ベータ）; （（λn.n* 2）7）→7 * 2
• η-変換：等価置換（eta）。 λx。（fx）→f

任意の順序で縮小し、同等の結果を得ることができることに注意してください。

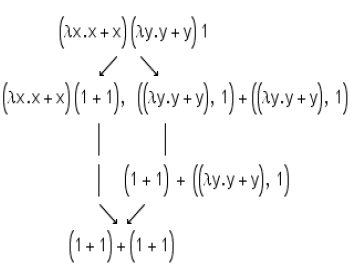
式を縮小できない場合、計算されたと見なされ、通常の形式になります。 計算は一連の単純化です。
1958年、ジョン・マッカーシーは、フォン・ノイマンのマシンで実行できるラムダ計算をLisp言語で実装します。 Lispはラムダ計算の実装であり、チューリングマシンではありません（gotoはありません）が、チャーチチューリングの論文によれば、それはそのようなマシンです。 Lispを練習する初心者はまず、関数型言語のプログラムの動作のシーケンスは一般に私たちにとって未知であり、重要ではないことを理解する必要があります。 Lispのコードとデータの表現は同じです-これは3つの操作で定義されたリストです

 (defun cons (ab) (lambda (f) (funcall fab))) (defun car (c) (funcall c (lambda (ab) a))) (defun cdr (c) (funcall c (lambda (ab) b))) 

スタックは次のように記述できます

 (let (stack) (defun push (x) (setq stack (cons x stack))) (defun pop () ;; note the usefulness of VALUES. (values (car stack) (setq stack (cdr stack))))) 

はい、チューリングのラムダ計算は同等ですが、型付けされていません。 用語の種類に制限を導入し、形式を一般化しますが、用語の概念の一般性を減らします。 型付きラムダ計算は一般にチューリング完全ではありません。

完全性を実現するには、追加の抽象化が必要です。 そして、1942-1945年に、アイレンバーグとマクレーンはそのような抽象概念、つまりカテゴリーの理論を作成しました。 教会はカテゴリー理論と呼ぶ

彼が見たすべての中で最高の数学的形式

カテゴリCに含まれる必要があります
カテゴリオブジェクトのクラスob（X）
射のクラスH（A、B）（または矢印f：a-> b）
二重操作∘、射の合成f∘g、f∊H（B、C）g∊H（A、B）→f∘g∊H（A、C）

• 連想：h∘（g∘f）=（h∘g）∘f
• および識別されたID：x→x
  id∘f = f = f∘id

ファンクタは、構造を保持するカテゴリマッピングです。

自然な変換は、2つのファンクターの比率です。

1970年代初頭、GirardとReynoldsは、System-Fを多相ラムダ計算として独自に定式化しました（概して、ラムダ表記の普遍性の数量化子を許可しました）。 HindleyとMilnerは、アルゴリズムOの複雑度O（1）を開発して、型を導出しました。つまり、式のサイズから線形になりました（このため、表記のプレフィックスを作成する必要がありました）。 MilnerはシステムをML言語に埋め込み、1990年までにHaskellに登場します。 したがって、Haskellでは、すべてのデータ型とすべての可能な関数を持つ射型を持つオブジェクトを含むHaskカテゴリを自由に使用できます。
Haskellの概念は、数学者Haskell Curryの考えを反映している。

証明はプログラムであり、証明される式はプログラムの一種です

このような形式での計算は、たとえば、宣言されたカテゴリの結論であり、計算の結果は証明の副作用と見なされます。
たとえば、べき級数で展開された指数の場合

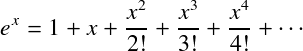
私たちは言うことができます

 integral fs = 0 : zipWith (/) fs [1..] --  (Fractional a, Enum a) => [a] -> [a] expx = 1 + (integral expx) --   

Algorithm-Wとエレガントな数学の焦点-モナドは、構造再帰の一般化として、フォンノイマンマシンでHaskカテゴリを実装することを可能にしました。 Haskellは、型チェッカーがWアルゴリズムを実装しているという理由だけでチューリング完全です。 ただし、この言語はチューリングマシンとして設計されたものではないことを理解してください。カテゴリの理論では、有限状態マシンが構築される状態の抽象化は存在しません。
実際には、Haskellの学生は、値（不変）ではなく、変数のタイプと変数間の射について話すことに慣れるのに役立ちます。

フォンノイマンのマシンはシーケンシャルコンピューターですが、これらのマシンはネットワークでの接続を学習しています。 1985年、Charles Hoareは「Communicating Sequential Processes」というドキュメントを発行し、そこで新しい形式を開発しました。 序文はダイクストラによって書かれています。
オブジェクトは、関連するイベントのアルファベットで記述されます。 そのようなイベントの全体がプロセスを形成します。
キューイングマシンを取る

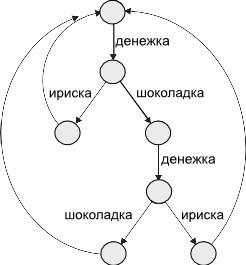
xをイベント、Pをプロセスとすると、次のようになります。

 (x → P ) 

（「x then P」と発音）は、最初にイベントxを発生させ、次にPのように動作するオブジェクトを記述します。

  = μX •  → ( → X |  → X) 

Xは変更可能なローカル変数です
オブジェクトによって渡されるイベントのシーケンスがプロセストレースを構成します。
プロセス環境もシーケンシャルプロセスと見なされます。
2つのプロセスが同じイベントをアルファベットで持つことができます

  = μX •( → X |  → X |  →  → X ) 

甘い歯はタフィーを無料で手に入れることを嫌うものではありませんが、奇跡はありません

 ( ||  ) = μ X • ( →  → X) 

このような表記法では、Hoarは「食事哲学者の問題」を効果的に解決（少なくとも診断）できる代数を構築し、この代数の法則を導き出します。

 L1 P||Q=Q||P L2 P ||(Q ||R)=(P ||Q)||R L3 (c →P)||(c →Q)=(c →(P ||Q)) ... 

形式主義は、Erlang、Golang、Ada Haskellライブラリおよびその他の言語で実装されています。
同じテープ上に植えられた2つのチューリング機械はチューリング機械ですか？

はい、Hoarは答えます。 代数をラムダ計算で宣言し、Lispで実装します。 これで、マシン上で実行されている1つのフォンノイマンが相互作用する連続プロセスを常に簡単に表すことができるという合意に達しました。 逆の問題である、相互作用する2つのプロセスの割り当ては決して簡単ではありません。
これは、Goの最初の10個の素数に対する競争的なふるいがどのように見えるかです。

 package main //  2, 3, 4, ...   'ch'. func Generate(ch chan<- int) { for i := 2; ; i++ { ch <- i // ,       . } } //    in   out, //    'prime'. func Filter(in <-chan int, out chan<- int, prime int) { for { i := <-in //   'in'. if i%prime != 0 { out <- i //  'i'  'out'. } } } func main() { ch := make(chan int) //   ch. go Generate(ch) //  Generate  . for i := 0; i < 10; i++ { prime := <-ch print(prime, "\n") ch1 := make(chan int) go Filter(ch, ch1, prime) // Filter  . ch = ch1 } } 

Erlang、Go、またはWebのみで競争力のあるプログラミングを行うという実用的な観点から、最初にプロセスの共通ア​​ルファベット（共有リソース）を決定することが重要です。 並列プログラミング用のツールキットを持つ言語は、このツールキットを使用するように促します。 任意のアルゴリズムを順番に実装でき、原則としてより効率的に実装できることを覚えておく必要があります。

そう、はい-説明された形式はチューリングと同等です。 しかし、チューリングを模倣して、別のフレームワーク内で1つのパラダイムを再構築することにより各プログラムでこれを証明することは、私にとって逆効果のようです。 チャーターで、彼らは他の誰かの修道院に行きません。 根本的に異なる計算モデルを公言する言語を採用するには、持続可能なスキル、メトリック、および設計パターンを修正する必要があります。