翻訳はMathematicaドキュメントとしてダウンロードできます。このドキュメントには、記事で使用されているすべてのコードが含まれています（アーカイブ、約5 MB）。はじめに
ロシア語には、他の多くの言語と同様に、同じ長さの単語がありますが、1文字だけが異なります。 これらの種類の単語ペアは、
メタグラムと呼ばれ
ます 。
次のように、いくつかの連続したメタグラムがあるとします。
オピニオン-粉砕-くすぶり-摩擦-討論-飲酒-群発-シェービング-徹夜それらはメタグラムの連鎖、または単語の連鎖を形成します。
ここから、
「はしご 」
というゲームが登場します。これは、1879年に
ルイスキャロルによって発明されました。
すべての最初の単語からそのようなチェーンを構成できることは明らかであり、いくつかの単語は、明らかに長いチェーンを生成するはずです。
この投稿では、ロシア語で構築できる単語のチェーンを分析し、最長のチェーンを見つけようとします。
ロシア語の単語のリストをインポートする
単語チェーンを構築して分析するには、ロシア語で出会える単語のリストが必要です。 この投稿では、使用できる品詞を制限しませんが
、単語
パラダイムの主格に対応する単語の形式のみを考慮し
ます 。 以前の投稿の1つ（
Wolfram言語（Mathematica）を使用して250の最高の映画のリストを表示するための最適なシーケンスを見つける ）のように、学者
Andrei Anatolyevich Zaliznyakによって作成されたロシア語の形態学的辞書：
[1]で：=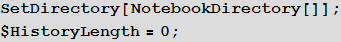
[3]で：=
辞書のデータを処理し、それに基づいてロシア語ロシア語の単語のリストを編集します
russianWords ：
[4]で：=
ワードチェーン内のリンクを定義する関数
chainLinkQ関数を作成してみましょう。この関数は、2つの単語が単語のチェーン内のリンクになるかどうかを判断します。つまり、この関数は、2つの単語がメタグラムであるかどうかの質問に答えます。
この場合、2つのオプションを検討します。
[5]で：=
[6]で：=
固定長単語のすべてのメタグラムの検索機能
これで、一連の単語（メタグラム）内のすべてのリンクが見つかりました。
まず、ロシア語のすべての単語を
同等クラスに分割し
ます 。つまり、実際には、ロシア語の単語の
因子セットをその長さで構築します。つまり、すべての単語のリストを1番目、2番目、 3、4など。
[7]で：=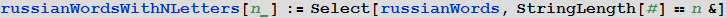
ロシア語の最小語長と最大語長を見つける：
[8]で：=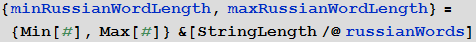
アウト[8] =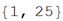
ロシア語の単語の長さの分布を見てみましょう：
[9]で：=
アウト[9] =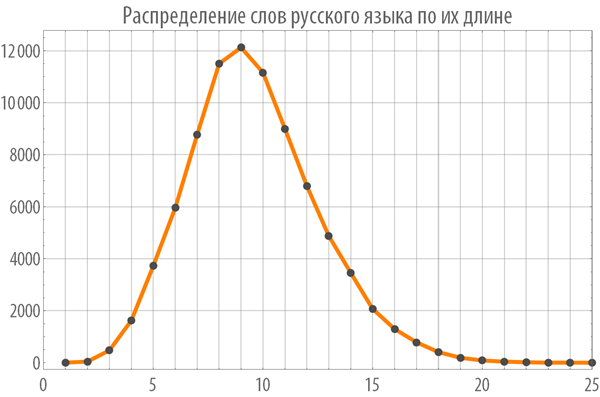
次に、計算値を保持する関数を作成します。この関数は、指定された長さの可能なすべての単語のペアの中から、ワードチェーンのリンクになり得るものを選択します。
[10]で：=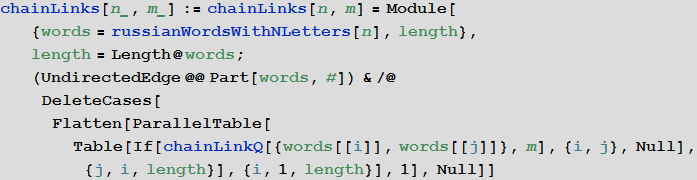
ロシア語の単語の等価クラスごとにこの関数を計算しますが、1文字だけ異なる単語のみを考慮します。
[11]で：=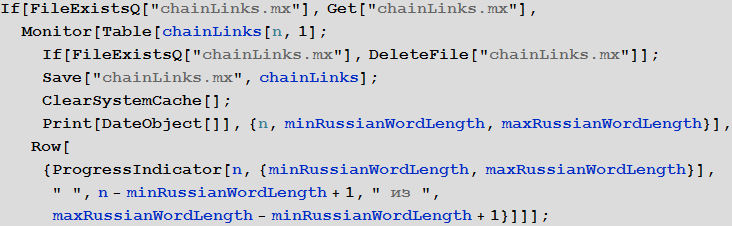
計算結果の例：
[12]で：=
アウト[12] =
ワードライングラフ
各等価クラスのワードチェーンのすべてのリンクの検索関数を計算した後、各タイプのワードチェーンの構造を視覚的に調べることができる対応するグラフを構築できます（グラフがない場合、この長さの単語のリンクはありません）。
グラフの各頂点にカーソルを合わせると、グラフの特定の頂点に対応する単語を含むツールチップを取得できます（投稿の冒頭にあるリンクからインタラクティブなグラフとソースコードを含むドキュメントをダウンロードできます）。
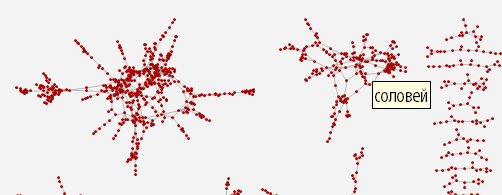[13]で：=
[14]で：=
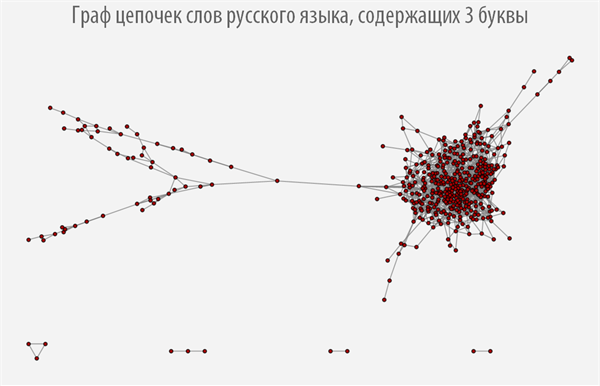
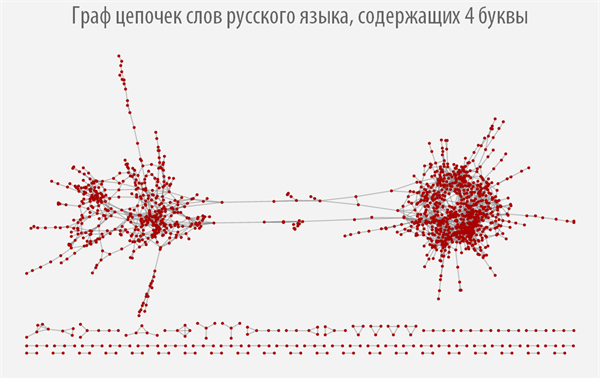
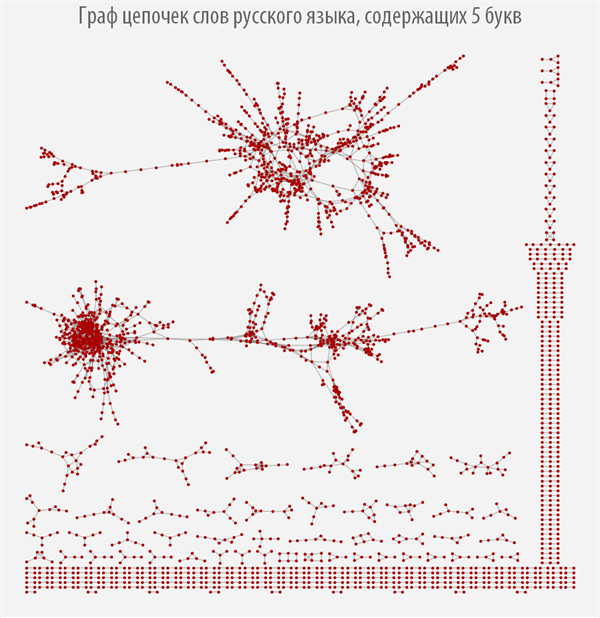
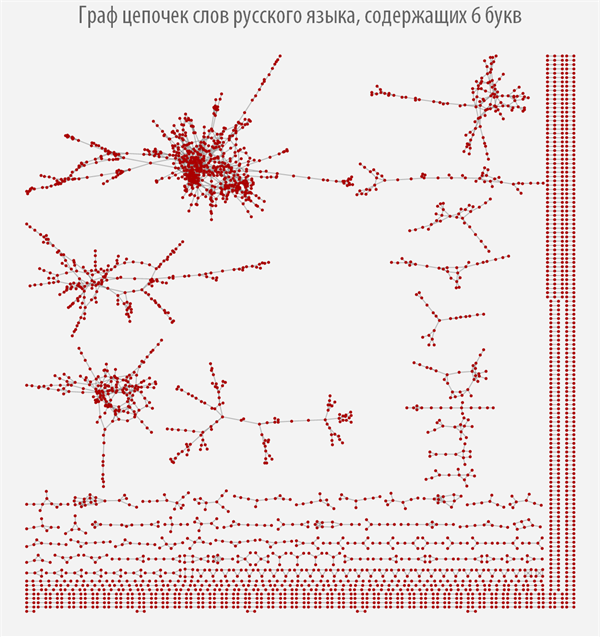
上記のグラフは、作成元の単語の長さに応じて構造がどの程度変化するかを示していますが、ほとんどのグラフには複数の連結コンポーネントがあることがわかります。
以下のグラフから、上記のすべてのグラフの中で異なる長さの連結成分の数の依存性を見ることができます。このことから、依存性は次の形式でなければなりません。
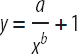
ここで、xは接続されたコンポーネントのサイズ、yは接続されたコンポーネントの数です。
[15]で：=
アウト[16] =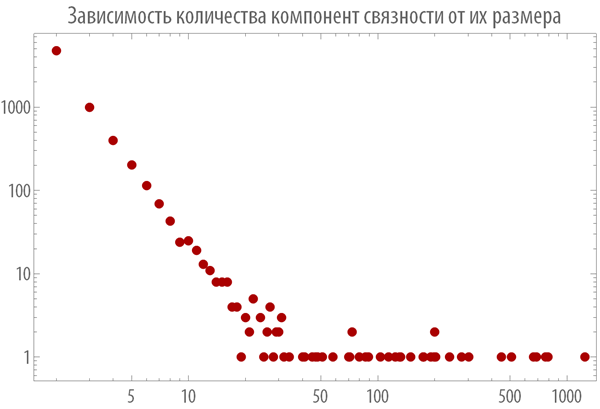
確かに：
[17]で：=
アウト[17] =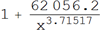
[19]で：=
アウト[19] =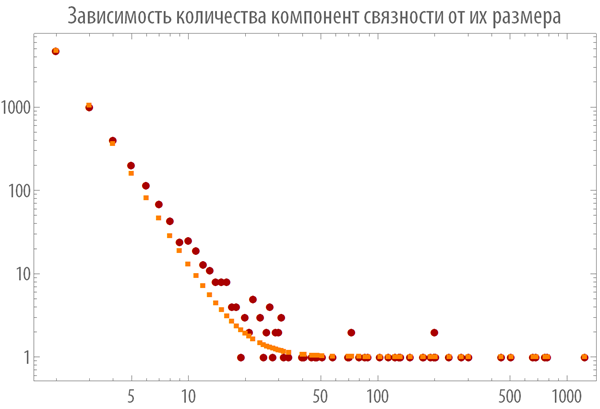
ロシア語の単語の連鎖に適用されるドナルド・クヌースの仮定
ドナルド・クヌースは 、コンピュータを使用して英語のチェーンを研究した最初の人の一人です。 彼は5文字からなる単語のチェーンを研究しました。これは、少数の文字、たとえば3からの単語は学習するには単純すぎると考えていたためです（ルイスキャロルは、APEという単語からMANという単語への6つのリンクのチェーンを構成していましたが）対応するグラフに多くの接続されたコンポーネントがあるためなど、より多くの文字が長いチェーンにつながることはありません。
ロシア語のチェーンに関するKnuthの仮定を検証しましょう。
以下のグラフは、チェーンの構築元となる単語の文字数が増えると、座標を持つポイントの位置がどのように変化するかを示しています。
{グラフの接続コンポーネントの数、グラフのエッジの数} 。
左上隅は、「理想的なグラフ」に対応します。このグラフには、接続されたコンポーネントが1つあり、最大数のエッジがあります。 明らかに、与えられた点に対して考慮中の軌跡の最も近い点に対応するグラフは、「最良」とみなすことができます。 自動的に検出された対応するポイントは、2つの赤い円でマークされ、5文字の単語のチェーンのグラフに対応します。
したがって、ドナルド・クヌースが英語の単語チェーンに対して行った仮定は、驚くには当たらないように、ロシア語にも当てはまると言えます。 おそらく、これは人間の心理学のかなり深く根付いた特性であり、それぞれ1本と2本の手のひらの指に対応する数字5と10に結びついています。
[20]で：=
アウト[25] =
ロシア語で単語の最長チェーンを検索します
だから、かなり長い道のりを歩いて、ロシア語に存在する最長の単語のチェーンを見つける準備ができました。 前のセクションから次のように、それは5文字の単語のチェーンの中にあるはずです。
[26]で：=
アウト[26] =
したがって、ロシア語で最も長い2つの単語のチェーンを取得しましたが、予想どおり、それらは5文字の単語のチェーンの「最良」列に含まれています。
ロシア語のn文字の単語の最長チェーンを検索する
前のセクションでは、ロシア語で最も長い単語のチェーンを検索し、40文字の5文字の単語のチェーンを2つ見つけました。
n文字の単語の可能な限り長いチェーンを見てみましょう。
[27]で：=
8文字を含むロシア語の単語のチェーン、少なくとも5単語 12文字を含むロシア語の単語のチェーン、少なくとも5単語 13文字を含むロシア語の単語のチェーン、少なくとも5単語 おわりに
私の投稿があなたの興味を引くことを願っています。そして、そこに提示されているアイデアやプログラムのいくつかがあなたに役立つことを願っています。 もちろん、ロシア語に関する多くの興味深い研究を思いつくことができます。 投稿の冒頭で、
chainLinkQ関数が作成されたとし
ましょう 。その機能により、2文字が異なるメタグラムの同様の調査が可能になります。これは、実際には、単語チェーンのゲームのルールの小さな変更に対応します。 以下に示す2つのグラフから、1文字だけが異なるメタグラムのグラフと比較して、2文字が異なる4文字のメタグラムのグラフがつながっていることが明らかです。 これは、そのようなグラフとチェーンの研究の結果が完全に異なることを示唆しています。
[28]で：=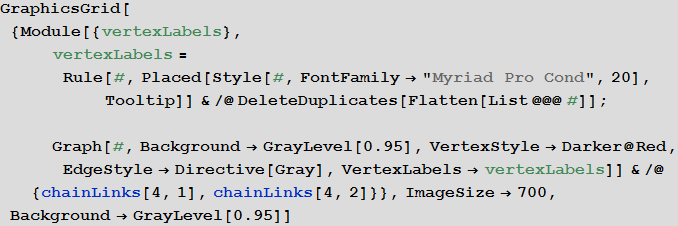
アウト[28] =
ロシア語でWolfram言語（ Mathematica ）を学習するためのリソース： http : //habrahabr.ru/post/244451