遺伝的アルゴリズムで遊ぶ

12月のある土曜日の夜、私はThe Blind Watchmakerの本を読んでいて、とても興味深い実験に打たれました。たとえば、シェークスピアの文字列のような文を考えてください ： Methinksはイタチと同じ長さのランダムな文字列です： wdltmnlt dtjbkwirzrezlmzco pとランダムな変更を開始します。 シェークスピアに似た子孫だけが生き残った場合、このランダムな文字列は何世代にわたってシェークスピア系統になりますか？

今日はこの実験を繰り返しますが、規模はまったく異なります。



記事の構造：

1. 遺伝的アルゴリズムとは何ですか？
2. なぜ機能するのか
3. ランダムな文字列で問題を形式化します
4. アルゴリズムの例
5. 古典的な実験
6. コードとデータ
7. 結論

注意トラフィック！

遺伝的アルゴリズムとは何ですか？

人工知能の分野では、 遺伝的アルゴリズムは自然selectionに基づく意思決定の発見的手法を指します。 原則として、検索スペースが非常に大きく、正確なソリューションを見つけることができず、ヒューリスティックなソリューションが要件を満たすタスクに使用されます。 タスク自体には、ソリューションの品質に関する何らかの機能があり、それを最大化する必要があります。

最も単純な形式では、遺伝的アルゴリズムの構造は次のとおりです（図を参照）。まず、何らかのソリューションから始めます。この場合、これはランダムな文字列です。 たとえば、文字列内のランダムに選択された文字をランダムに選択された文字に変更し、新しい文字列のセットを取得します（文字列ごとにk個の変異）。 それらから、シェイクスピアのものに近い（一致する文字の数で）ものだけを選択します。たとえば、このような10行は、シェイクスピアのものが含まれていない場合、プロセスを再び開始します。

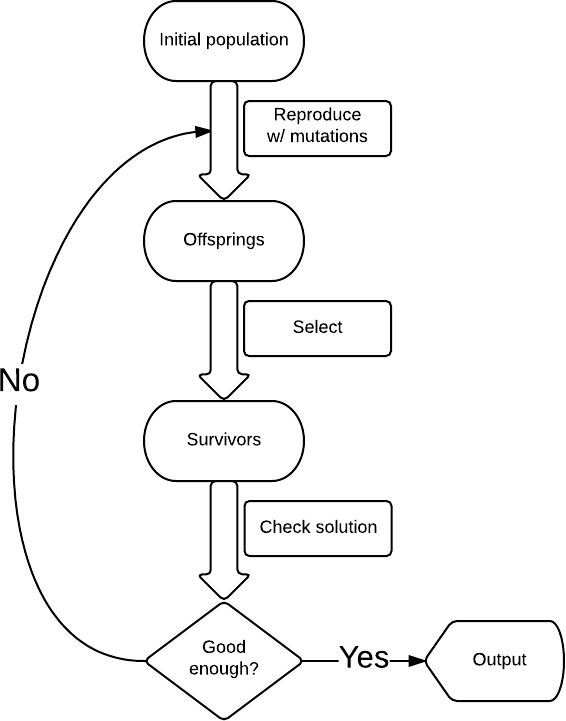
なぜ機能するのか

多くの点で、遺伝的アルゴリズムは古典的な最適化手法に似ています。母集団は現在の点の集合、突然変異は隣接点の研究、選択は限られた計算リソースの条件で解を見つけるための新しい点の選択です。

現在の検索ポイントを最大値として選択するため、人口は常に最も近い最大値になります（他のすべてのポイント「ダイ」は、最も近い最大値との競合に耐えられません）。 母集団のサイズは重要であるため、最大方向への少なくとも1ステップの確率は無視できないことを意味するため、一定のステップ数の後、母集団は極大に向かって移動します。 そして、最大値に近づいたポイントの子孫は、「生存」が大きくなります。 したがって、十分な数のステップの後、このポイントの子孫が母集団を支配し始め、すべてが最大にシフトします。

極大値になりがちな母集団の視覚化：


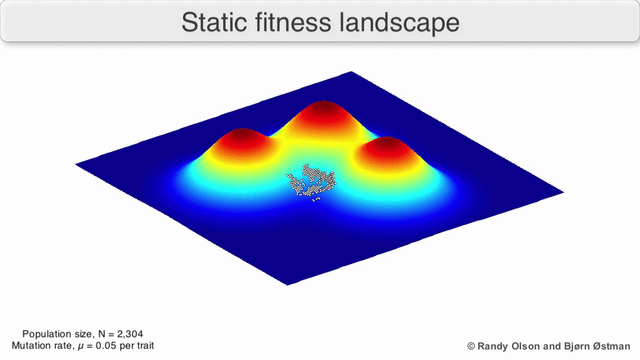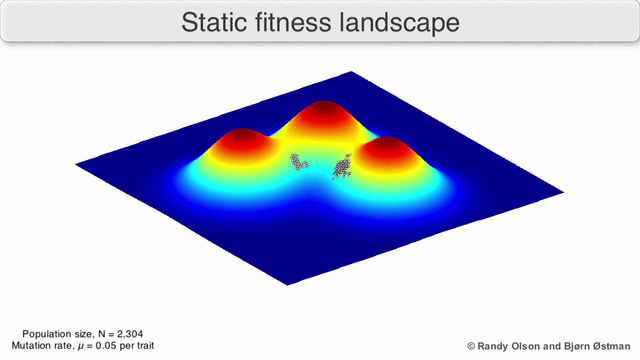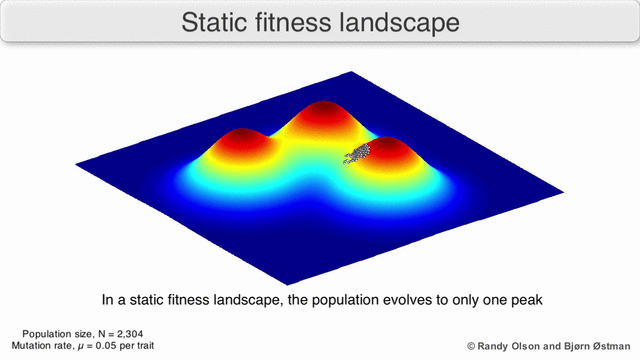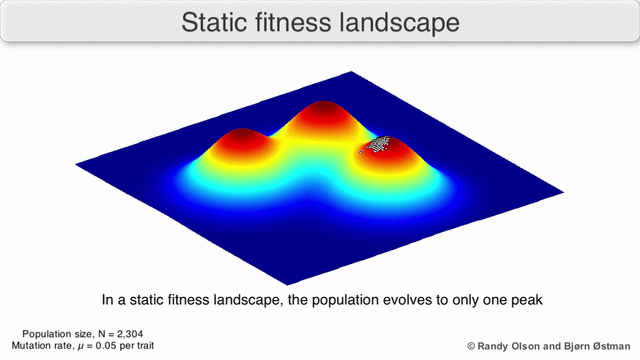
（ ランディオルソンによる ）

ランダムな文字列で問題を形式化します

入力 ：文字列S
出力 ：長さlen（ S ）のランダム文字列を文字列Sに変換するのに必要な世代数に等しい自然数N

私たちの場合の突然変異とは何ですか？ 文字列Sを変更することにより、文字列Sからランダムに選択された1つの文字をアルファベットの別の任意の文字に置き換えることを意味します。 このタスクでは、小文字のラテン文字とスペースのみを使用します。

初期集団 （スキームの初期集団）とは何ですか？ これは、入力文字列Sと長さが等しいランダムな文字列です。

子孫とは何ですか？ 定数kごとに1行の突然変異の数を修正すると仮定すると、子孫は現在の世代の各行のk個の突然変異です。

生存者とは何ですか？ 母集団のサイズを定数hで固定すると、生存者は入力ラインSにできるだけ近いhラインになります。

擬似コード（恐らくpythonに似ています）では、次のようになります。

アルゴリズムの例

次の行を考えてみましょう：速い茶色のキツネは怠laな犬を飛び越えて、そのためのプログラムの出力を再現します：
変更のチェーン（左側の世代番号）を考慮してください。

 1 rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquvmopyk
 2 rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquzmopyk
 3 rbb mffwfhwtxnjjiozz ujhhlxeoyhezarquzmopyk
 4 rbb mffwfhwtxnjjiozz ujhhlxeoyhezarquzmodyk
 5 rbb mffwfhbtxnjjiozz ujhhlxeoyhezarquzmodyk
 6 rbb mffcfhbtxnjjiozz ujhhlxeoyhezarquzmodyk
 7 rbb mffcf btxnjjiozz ujhhlxeoyhezarquzmodyk
 8 rbb mffcf btxnjjiozz ujhhlxeoyheza quzmodyk
 9 rbb mffcf brxnjjiozz ujhhlxeoyheza quzmodyk
 10 rbb mffcf brxnjjiozz ujphlxeoyheza quzmodyk
 20 rbb mffcf bronj fox jujpslxveyheza luzmodyk
 30 rbb mficf bronj fox jumps overhehe luzy dyg
 40彼はミックブロンフォックスが怠zyな犬を飛び越える
 41彼はリックブロンフォックスが怠zyな犬を飛び越える
 42彼はリックブロンフォックスが怠zyな犬を飛び越える
 43怠qな犬を飛び越える茶色のキツネ
 44彼は怠brownな犬の上を素早く茶色のキツネが飛び越える
 45アヘクイックブラウンフォックスは怠aな犬を飛び越える
 46速い茶色のキツネが怠zyな犬を飛び越える

ご覧のとおり、各世代の違いは1つだけです。 rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquvmopykから、突然変異と選択を経て怠brownな犬の上を素早く茶色のキツネがジャンプするまでに合計46世代かかりました 。

古典的な実験

個々の例、シェークスピアのラインまたはキツネに関する英語のパングラムは興味深いですが、あまり説得力がありません。 したがって、私はより興味深い質問を検討することにしました。古典的な作品をいくつか取り、それらを文に分割し、それぞれの世代数を計算するとどうなりますか？ 世代数が文字列に依存する性質はどうなりますか（たとえば、その長さ）。

ハーパー・リーの「モックバードを殺す」（モッキンバードを殺す、ハーパー・リー）と、JDサリンジャーの「ライでキャッチャー」（ライのキャッチャー、JDサリンジャー）をクラシック作品として選びました。 2つのパラメーターを測定します-文による世代数の分布と、行数に対する世代数の依存性（相関関係はありますか？）。

パラメーターは次のとおりです。行の子孫の数：100。 世代の生存者数：10。

結果

ご覧のように、大部分の文は十分に速く行に到達することができ、100回未満の反復で200回の反復が可能です（すべての文のうち、文で判断して1,135回の反復が必要なのは1つだけであり、ブレークダウンアルゴリズムはミスを犯して複数の文を1つに接着しました） ）：



文字列の長さと世代数の間の相関関係は完全です。 これは、ほぼすべての世代がターゲットラインに一歩近づいたことを意味します。


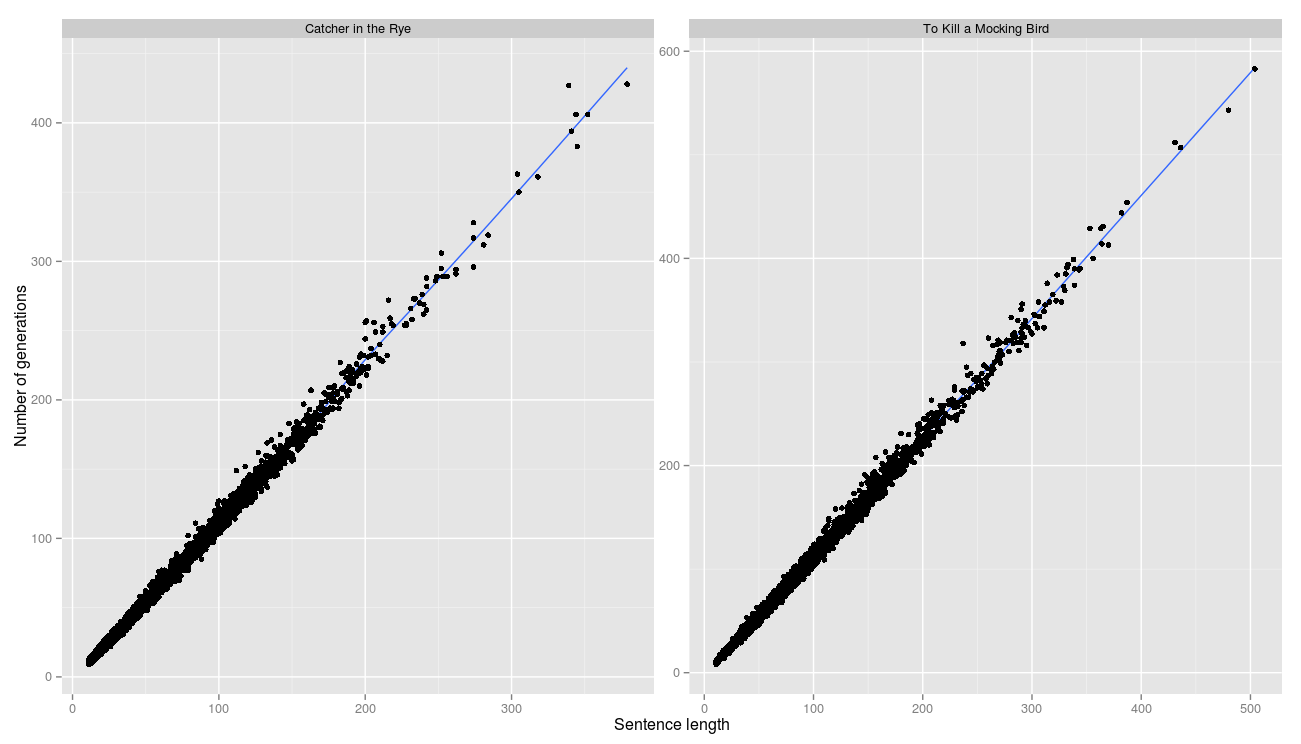
R ^ 2はそれぞれ0.996と0.997です。

したがって、任意の入力文字列Sの問題の条件下で、世代数が文字列の長さに線形に依存することが実験的に確立されました。これは初期の仮定と一致しています。

コードとデータ

すべてのコード、python-遺伝的アルゴリズム\テキスト処理およびR-視覚化、githubで利用可能：
github.com/SergeyParamonov/genetics-experiments

結論

遺伝的アルゴリズムの基本構造を把握し、文字列突然変異を適用して問題を解決しました。 古典的なテキストを使った実験の結果、我々の条件では、文字列の長さと入力文字列に到達するのに必要な世代数との間に線形関係があることがわかりました。

また、基本的な検索構造を変更して（たとえば、 クロスオーバーを使用して、複数の生成メンバーを使用して子孫を作成する）、正確な解を見つけるのが非常に困難な幅広いクラスの最適化問題を解決できることに注意しました。