先に投稿を約束したように、画像圧縮に関する大規模なストーリーの第2部を紹介します。今回は、ロスレス画像圧縮方式に焦点を当てます。

バイナリ圧縮

シリーズの長さのエンコード方法

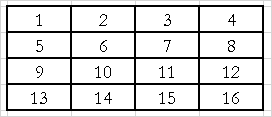
理解する最も簡単なアルゴリズムは、1950年代に開発されたシリーズの長さのコーディングアルゴリズムです。アルゴリズムの主なアイデアは、バイナリイメージの各ラインを、黒と白のピクセルの連続したグループの長さのシーケンスとして表すことです。たとえば、図に示す画像の2行目 1は次のようになります：2,3,2。しかし、デコードプロセスでは、あいまいさが発生します。どのシリーズかは明確ではありません。最初の数字は黒または白をエンコードします。この問題を解決するには、2つの明白な方法があります。最初に各行の最初のピクセルの値を示すか、各行の白いピクセルのシーケンスの長さを最初に示すことに同意します（ゼロにすることができます）。

シリーズの長さをコーディングする方法は、特に単純な構造の画像に対して非常に効果的ですが、この方法は、ハフマン法などのエントロピーアルゴリズムによって得られたシーケンスをさらに圧縮すると、大幅に改善できます。さらに、エントロピーアルゴリズムは、黒と白のシーケンスに対して個別に個別に使用でき、圧縮の程度がさらに向上します。

パスエンコーディング方法

符号化系列の長さの概念のさらなる発展は、輪郭追跡圧縮法です。この方法は、圧縮イメージの高レベルプロパティの使用に基づいています。つまり画像は単なるピクセルのセットとしてではなく、前景と背景のオブジェクトとして認識されます。圧縮は、オブジェクトを効率的に表現することにより実行されます。プレゼンテーションにはさまざまな方法がありますが、図の例で後で検討します。 2。

まず、各オブジェクトの説明は、オブジェクトの開始と終了の特別なメッセージ（タグ）で囲まれる必要があることに注意してください。最初の最も簡単な方法は、各線の輪郭の開始点と終了点の座標を指定することです。図の画像 2は次のようにエンコードされます。

<開始>
ページ 2 4-8
ページ 3 3-8
ページ 4 3-8
<終了 >
<開始>
ページ 6 2-8
ページ 7 2-9
ページ 8 2-9
ページ 9 2-9
<終了 >

もちろん、このレコードは、以前に検討したアルゴリズムを使用してさらに圧縮されます。ただし、ここでもデータを変換して、さらに圧縮率を高めることができます。このために、いわゆるデルタコーディング：境界の即時座標を記録する代わりに、前のラインに対するオフセットが記録されます。デルタコーディングを使用すると、図 2は次のようにエンコードされます。

<開始>
ページ 2 4、8
ページ 3-1、0
ページ 4 0、0
<終了 >
<開始>
ページ 6 2、8
ページ 7 0、1
ページ 8 0、0
ページ 9 0、0
<終了 >

デルタコーディングの効率は、変位の値がゼロに近いモジュロであり、その記述に多数のオブジェクトがある場合、ゼロおよびゼロに近い値が多くなるという事実によって説明されます。この方法で変換されたデータは、エントロピーアルゴリズムによってはるかに圧縮されます。

永続化コーディング

バイナリ画像の圧縮に関する会話を締めくくるには、別の方法-永続化領域のコーディング-に言及する必要があります。この方法では、画像はn ₁ * n ₂ピクセルの長方形に分割されます。結果の長方形はすべて、完全に白、完全に黒、混合の3つのグループに分けられます。最も一般的なカテゴリは1ビットのコードワードでエンコードされ、他の2つのカテゴリは2ビットからコードを受け取ります。この場合、混合領域のコードはラベルとして機能し、その後に長方形を記述するn ₁ * n ₂ビットが続きます。図のよく知られた画像を分割すると正方形あたり2 * 2ピクセル、5つの白い正方形、6つの黒と13の混合を取得します。混合正方形のラベルに0、11が白い正方形のラベル、10が黒い正方形のラベルにそれぞれ同意します。単一の白いピクセルはそれぞれ1、黒は0にエンコードされます。その後、画像全体は次のようにエンコードされます（太字）：

ほとんどの圧縮方法と同様に、この方法の効率は元の画像が大きいほど高くなります。さらに、混合正方形の値は、辞書アルゴリズムによって非常に効率的に圧縮できることに注意できます。
これで、バイナリ圧縮に関する話は終わりです。フルカラー画像とモノクロ画像の可逆圧縮の話に進みます。

モノクロおよびフルカラー圧縮

ロスレス画像圧縮にはさまざまなアプローチがあります。最も簡単なものは、前の記事で説明したアルゴリズムを直接適用することです;他のより高度なアルゴリズムは、圧縮可能なデータのタイプに関する情報を使用します。

ビットプレーンエンコーディング

最初の方法は、ビットプレーンのコーディングと呼ばれる方法です。 n個の輝度レベルを持つ任意の画像を考えます。明らかに、これらのレベルはlog ₂ nビットを使用して表すことができます。ビットプレーンに分解する方法は、n個の輝度レベルを持つ1つの画像をlog ₂ n個のバイナリ画像に分割することです。この場合、i番目の画像は、元の画像の各ピクセルからi番目のビットを抽出することによって取得されます。タブで。図1は、ビットプレーンでの元の画像の分解を示しています。

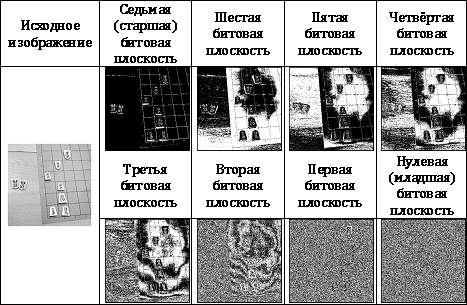
画像がビットプレーンに分解された後、結果の各画像は、前述のバイナリ画像圧縮方法を使用して圧縮できます。

このアプローチのかなり明らかな欠点は、輝度のわずかな変化を伴う放電の多重転送の効果です。たとえば、明るさを127から128に変更すると、すべてのバイナリビット（0111111→10000000）の値が変更され、すべてのビットプレーンが変更されます。

複数の転送の悪影響を減らすために、実際には、2つの隣接する要素が1つのカテゴリでのみ異なるグレーコードなど、特別なコードが実際に使用されることがよくあります。 nビットの数値をグレイコードに変換するには、同じ数値を1ビット右にシフトしてビット単位の排他的OR演算を実行する必要があります。グレイコードからの逆変換は、元の数値のすべての非ゼロオフセットに対してビットごとの排他的OR演算を実行することにより実行できます。グレイコードとの間で変換するためのアルゴリズムをリスト1に示します。

関数 BinToGray （ BinValue ： byte ）：バイト ;
始める
BinToGray ： = BinValue xor （ BinValue shr 1 ） ;
終わり ;

関数 GrayToBin （ GrayValue ： byte ）：バイト ;
var
BinValue ：整数 ;
始める
BinValue ： = 0 ;
一方、 GrayValue> 0 は
始める
BinValue ： = BinValue xor GrayValue ;
GrayValue ： = GrayValue shr 1 ;
終わり ;
GrayToBin ： = BinValue ;
終わり ;

グレーコードへの変換後、明るさを127から128に変更するときに、1つのバイナリビットのみが変更されることを確認するのは簡単です。

グレイコードを使用して取得されたビットプレーンはより単調であり、一般に圧縮率が高くなります。タブで。 2は、元の画像とグレーコードに変換された画像から取得したビットプレーンを示しています。

予測コーディング

予測コーディングは、デルタコーディングアルゴリズムに似たアイデアに基づいています。ほとんどの実際の画像は局所的に均質です。ピクセルの隣接ピクセルは、ピクセル自体とほぼ同じ明るさです。この条件は、オブジェクトの境界では満たされていませんが、ほとんどの画像では真実です。これに基づいて、ピクセルの輝度値は、近傍の輝度に基づいて予測できます。もちろん、この予測は完全に正確ではなく、予測エラーが発生します。その後、エントロピーアルゴリズムを使用してエンコードされるのは、この予測エラーです。符号化効率は、すでに述べた局所均一性の特性によって保証されます。画像のほとんどでは、モジュロ誤差の値はゼロに近くなります。

このエンコード方式では、エンコードとデコードの両方に同じ予測子を使用することが非常に重要です。一般的な場合、予測子は画像のあらゆる特性を使用できますが、実際には、予測値はほとんどの場合、近傍の明るさの線形結合として計算されます：p _k = ∑ _{i = 1} _Mαi * p _ki この式では、Mは予測に関与する近傍の数（予測順序）、インデックスpは表示される順序のピクセル数です。 M = 1の場合、予測コーディングは以前に考慮されたデルタコーディングに変わります（ただし、座標差の代わりに輝度差がエンコードされます）。

ここでは、ピクセルの表示順序について少し説明する必要があります。ここまで、ピクセルは左から右、上から下、つまり、ライントラバーサル順（表3）：

しかし、4番目のピクセルに基づいて5番目のピクセルの輝度を予測した結果（ラインを移動するとき）は、真の結果から非常に遠くなることは明らかです。したがって、実際には、他のバイパス順序がしばしば使用されます。たとえば、スプレッド、スネーク、ストライプ、スプレッド付きのストライプなどのバイパスです。リストされている回避策の一部を表にリストします。 4

特定の例を使用して、説明した方法を検討してください。図のオスタンキノテレビ塔の画像に予測コーディングを適用してみましょう。 3

簡単にするために、1次予測（デルタコーディング）と行単位の走査（各行は個別にエンコードされます）を使用します。ソフトウェア実装では、値を予測できない最初のMピクセルに関する情報を送信する方法を決定する必要があります。リスト2の実装は次のアプローチを使用します。各行の最初のピクセルはその輝度値によって直接エンコードされ、行内の後続のすべてのピクセルは前のピクセルに基づいて予測されます。

タイプ
TPredictionEncodedImg = 整数の配列の配列。
関数 DeltaEncoding ： TPredictionEncodedImg ;
var
r ： TPredictionEncodedImg ;
i 、 j ：単語。
始める
SetLength （ r 、 GSI。N + 1 ） ;
for i ： = 1 から GSI N do
始める
SetLength （ r [ i ] 、 GSI。M + 1 ） ;
r [ i 、 1 ] ： = GSI i [ i 、 1 ] ;
終わり ;
for i ： = 1 から GSI N do
for j ： = 2 to GSI 。 M do
r [ i 、 j ] ： = GSI i [ i 、 j ] -GSI 。 i [ i 、 j - 1 ] ;
DeltaEncoding ： = r ;
終わり ;

タブで。 5はこのアルゴリズムの結果を示しています。正確に予測されたピクセルは白で表示され、エラーは色でマークされ、正のエラー値は赤で、負の値は緑で表示されます。色の強度は、エラー値のモジュラスに対応します。

分析によると、このような実装では、わずか0.21の輝度レベルの平均予測誤差しか得られません。高次予測およびその他のバイパス方法を使用すると、予測エラーがさらに減少するため、圧縮率が向上します。

ロスレス画像圧縮