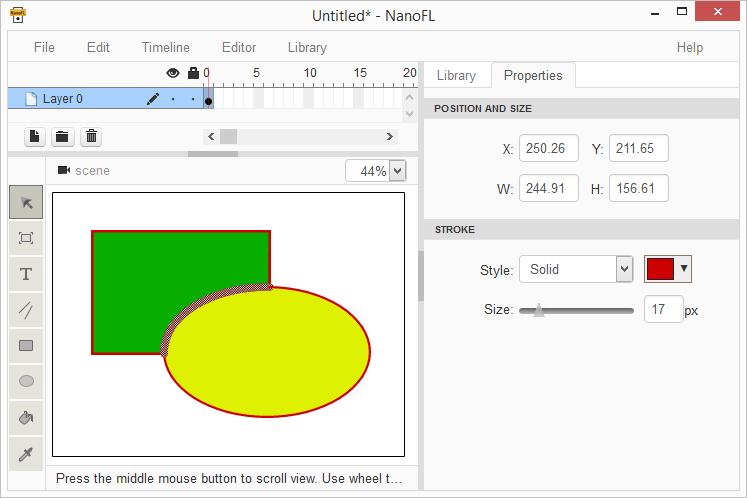
 前の記事
前の記事では、利用可能なすべてのセグメントを交差点で分割し、交差するセグメントがないことを保証しました。 このパートでは、取得したセグメントを等高線に結合し、その塗りつぶしを決定します。
輪郭検索
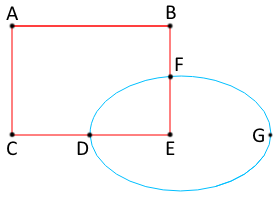
そのため、互いに素なセグメントのセットがあります。 ポリゴンを識別するのに役立つ輪郭を探してみましょう。 右側の図には、6つの赤いセグメントと3つの青いセグメントがあります。 ABFDC、DFE、およびFGDの輪郭を見つけられると便利です。 複合ループ(たとえば、ABFGDC)は関心がありません。つまり、原則としてアルゴリズムがループにつまずかないか、これらのループを後で除外する必要があります。
検索で検索

私の頭に浮かんだ最初のアルゴリズムは、最初から現れていました。 これは次のようなものです。
- 簡単にするために、セグメントの数を2倍にして、各セグメントに逆方向のクローンを追加します(これにより、セグメントを「後方」に歩くことなく、ベクトルとしてセグメントに沿って歩くことができます)。
- 必要な輪郭の最初のセグメントとして各セグメントを連続して取得し、新しい配列に配置して、再帰的検索手順を呼び出します(以下)。
- 最初に最後に見つかったセグメントに結合し、そのエンドポイントが配列内のセグメントのポイント間でまだ検出されていないセグメントを探して、すべてのセグメントをソートし、配列の最後に追加します。
- このセグメントの終わりが配列の最初のセグメントの始まりと一致する場合-つまり、輪郭が見つかった-見つかった輪郭の配列にセグメントの配列を追加し、再帰を終了します。
- そうでない場合は、次のセグメントの検索プロシージャを再帰的に呼び出します。
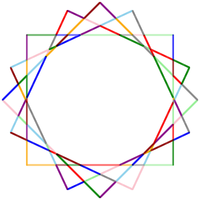
このアルゴリズムに複合ループを除去する手順を追加することにより、非常に実行可能なものを得ることができます。 そして、私は実際の状況に出くわすまではすべてがうまくいったと思いました(写真を参照)。 有名なキャラクターのチェーンにある黄色の「星」に注意してください。 中心を中心に回転した多数の正方形を重ねることで描画されます。 交差点でセグメントを分割した後、最初のセグメントはすでに112個です。 この画像での輪郭検索手順の終了を待つことに成功しませんでした。 しかし、実際、このようなセグメント数の徹底的な検索の推定時間はO(n!)であり、ご存じのように12セグメントでは正常ですが、100セグメントでは完全に受け入れられません。 別のアルゴリズムについて考えなければなりませんでした。
「極端な」セグメントを選択することによる方向検索

元の図面に戻りましょう(左側に複製されています)。 将来の輪郭の次のセグメントを探して、点Bから点Fへのベクトルに沿った場合、点Dまたは点Gのいずれかに移動するのは理にかなっています。 ベクトルFEに沿って移動する場合、明らかに複合輪郭に属するセグメントを選択します! つまり 少なくとも、すでに検索を大幅に減らすことができます(各ポイントから最大2つの方法を使用できます)。 これは良いことですが、さらに考えてみましょう。 上記のブルートフォースアルゴリズムでは、すべての輪郭が2回検出されます(1回-時計回りに移動し、別の時間-セグメントに沿って反時計回りに移動する)。 各ブランチで時計回りの動きの意味で最も極端なセグメントのみを選択するとどうなりますか? (例:最後のセグメントベクトルがBFの場合、次はFDになります。)必要なすべての輪郭が見つかります! 再帰なし! 奇跡!
ここで言及する価値があるのは、時計回りに移動しますが、開始ベクトルセグメントが右移動の輪郭に属していない場合、左移動(反時計回り)の輪郭が見つかる場合があることです。 さらに、これらの左輪郭は複合することができます(図では、ベクトルABは右輪郭ABFDCに属し、ベクトルBAは複合左輪郭BACDGFに属します)。したがって、結果の配列からすべての左輪郭を除外する必要があります。
パスが正しいかどうかを判断する方法は次のとおりです(ここで(x1、y2)はセグメントの開始点、(x3、y3)は終了点です)。
function isClockwise() { var sum = 0.0; for (edge in edges) { sum += (edge.x3 - edge.x1) * (edge.y3 + edge.y1); } return sum >= 0; }
結果として得られるアルゴリズムは既に許容可能な速度(Oのオーダー(n ^ 2)、私が理解している限り。正しくない場合は修正済み)で動作し、実際のタスクで完全に表示されます。 そして次に進みます。
見つかった輪郭によるポリゴンの識別
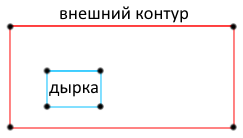
だから、輪郭があります。 それらをポリゴンに入れるときです(ポリゴンは外部輪郭+内部輪郭のセット-「穴」であることを思い出してください)。 タスクは「正面から」うまく解決されています。
- 将来のポリゴンの外部輪郭の各輪郭を順番に取得します。
- 残りの回路の中で、外部回路内にあるものを探しています。
- 外側の輪郭の内側にあるが、その「穴」の外側にある点を取ります。
- 元の画像で、この時点で塗りつぶし(つまり、それが属する多角形を探します)、そのような多角形が配置されている場合、元の画像で見つかった配列に外側の輪郭+「穴」を新しい多角形として追加します。
- 同様に、最終画像について(ポイントが属するポリゴンを探し、もしそうであれば、最終画像用に見つかった配列に新しいポリゴンを追加します)。
したがって、すべてのセグメントが交差した後の初期画像と最終画像を「再構築」します。 そして、元の画像の各ポリゴンが、オーバーレイ画像の同じポリゴンと一致するか(座標の意味で)、すべてのポリゴンを超えて広がることが保証されています。
項目3に特に注意を払う価値があると思います。 内側の輪郭の外側の輪郭の内側で良い点を取得するにはどうすればよいですか? そもそも、任意の方向に放出されたビームがポリゴンセグメントと奇数回交差したときに、ポイントがポリゴンの内側にあることを理解する必要があります。 そして、計算の精度が限られているために、すべてがうまくいき、ビームはセグメントの接合部に到達し、入射を引き起こす可能性があります(両方のセグメントとの交差を検出します) ほとんどの場合、計算を簡単にするために、ビームは水平方向に放出されます。 同じことをします。 良い点について私たちが今知っていることは次のとおりです。
- ポリゴンを構成するセグメントの端のいずれとも一致してはなりません(一致しないほど良い)。
- ポイントから放射される光線とこれらの同じセグメントの交差の検出に関連する問題の可能性を減らすために、ポイントはポリゴンのセグメントからより遠くにあることが望ましい。

そのような点の
y座標を見つけるための次のアルゴリズムが思い浮かびます。
- ポリゴンを構成するセグメントの端のすべてのy座標を配列に挿入します。
 外側の輪郭のminYとmaxYを追加します(これらの値はセグメントの端の値と必ずしも一致しないため、右の図を参照してください)。
外側の輪郭のminYとmaxYを追加します(これらの値はセグメントの端の値と必ずしも一致しないため、右の図を参照してください)。- 配列を昇順で並べ替えます。
- 差y2-y1が最大になる値(y1、y2)のシーケンシャルペアを配列で探しています。
- 目的のポイントのy座標について、これらの値の算術平均を取ります: y =(y1 + y2)/ 2 。
x座標の便利な値を見つけることは残っています。 これを行うには:

- 点(-infinity; y)から右に水平光線を放出します。
- 光線と多角形のセグメントの交点のすべてのx座標を見つけます。
- 昇順に並べ替えます。
- ペア(x [i]、x [i + 1])の中から選択します。ここで、 i = 0,2,4 ...差x [i + 1]-x [i]が最大になるものです。
- 目的のポイントのx座標について、このペアの算術平均を取ります: x =(x [i] + x [i + 1])/ 2 。
結果のアルゴリズムは完全ではありませんが、十分に単純であり、実践が示すように、実際のタスクでうまく機能します。
最後のステップ
この記事では、イメージユニオン検索アルゴリズムの残りの点については詳しく検討しません。
- オーバーレイ画像の影付き領域内に完全に収まった元の画像のすべてのエッジの削除。
- 色に関係なく、オーバーレイイメージで使用可能なすべてのポリゴンのソースイメージから削除します。
- 元の画像のエッジとポリゴンにオーバーレイ画像のすべてのエッジとポリゴンを追加します(この場合、元の画像の一致するエッジはオーバーレイのエッジで上書きされます)。
- 同じ塗りつぶしを持ち、エッジによる明確な分離がないポリゴンに隣接する元の画像を結合します。
これらのサブタスクは十分に簡単で、読者は(必要に応じて)自分で簡単にこれを処理できると思います。
おわりに
記事では、ベクトル画像を結合するための検索に関連するいくつかの興味深い点を示しました。 一部の機能は、次のように舞台裏に残りました。 それらが小さすぎるか、著者がそれらを忘れてしまいました。 記事と説明されているアルゴリズムの両方の説明に喜んでいます。