MATLABコードを固定小数点に転送するための最良のアプローチ

プロジェクトを浮動小数点から固定小数点に変換する場合、エンジニアは固定小数点で最適なデータ型を決定する必要があります。 これらのデータ型は、組み込みハードウェアの制限を満たしつつ、精度計算のシステム要件を満たしている必要があります。 Fixed-Point Designerは、固定小数点アルゴリズムを開発し、アルゴリズムを浮動小数点から固定小数点に変換し、固定小数点でのデータ型と算術属性を自動的に提案するのに役立ちます。 同時に、ビットに対して正確な固定小数点でのシミュレーション結果と浮動小数点での参照結果を比較することができます。

この記事では、MATLABコードを変換用に準備し、MATLABコードを固定小数点に直接変換し、効率とパフォーマンスのためにアルゴリズムを最適化するためのベストプラクティスを提供します。 後続の手動コーディングのためにMATLABの固定小数点でアルゴリズムを開発する場合、または自動コード生成のために固定小数点に変換する場合、説明されている手法は、汎用MATLABコードを効率的な固定小数点コードに変換するのに役立ちます。

固定小数点への転送のためのコードの準備
スムーズな変換プロセスを確保するには、次の3つの手順を実行する必要があります。

1. メインアルゴリズムを残りのコードから分離します。
2. インストルメンテーションとアクセラレーションのコードを準備します。
3. 固定小数点サポートに使用される関数を確認してください。

メインアルゴリズムと残りのMATLABコードの分離
通常、アルゴリズムには、入力データを準備するコードと、結果を検証するグラフを作成するコードが付属しています。 アルゴリズムコアのみを固定小数点に変換する必要があるため、別のテストファイルが入力を作成し、メインアルゴリズムを呼び出して結果をプロットするようにコードを構成する方が効率的です。 この場合、メインアルゴリズムも1つまたは複数の個別のファイルに格納されます（表1）。

元のコード	変更されたコード
% x = randn(100,1); % y = zeros(size(x)); y(1) = x(1); for n=2:length(x) y(n) = y(n-1) + x(n); end % yExpected = cumsum(x); plot(y-yExpected) title('')	テストファイル。 % x = randn(100,1); % y = cumulative_sum(x); % yExpected = cumsum(x); plot(y-yExpected) title('') アルゴリズムを含むファイル。 function y = cumulative_sum(x) y = zeros(size(x)); y(1) = x(1); for n=2:length(x) y(n) = y(n-1) + x(n); end end

表1.テストバインディングからメインアルゴリズムを分離する前後のコード。

計測と加速のためのアルゴリズムコードの準備
計装と加速により、変換プロセスが簡素化されます。 Fixed-Point Designerを使用して、コードを計測し、すべての名前付き変数と中間変数の最小値と最大値を記録します。 このツールは、記録された値を使用して、固定点でコードで使用するデータ型を提案できます。

Fixed-Point Designerを使用して、MEXファイルを作成することにより、固定点でアルゴリズムを高速化し、元のバージョンに対して固定点で実装を検証するために必要なシミュレーションを高速化することもできます。

インストルメンテーションとアクセラレーションはコード生成技術に依存しているため、使用する前に、CコードまたはHDLコードを生成するためにMATLAB CoderまたはHDL Coderを使用する予定がない場合でも、コード生成用のアルゴリズムを準備する必要があります。

最初に、コード生成でサポートされていない関数またはコンストラクトをMATLABコードで定義する必要があります（ サポートされている関数とオブジェクトのリストについては、 言語サポートを参照してください）。

この手順を自動化する方法は2つあります。

• ディレクティブを追加

   %#codegen 

  アルゴリズムのコアを含むMATLABファイルの先頭。 このディレクティブは、コード生成のためにサポートされているMATLAB言語のサブセットに含まれていない関数と構成を記録するようコードアナライザーに指示します 。
• コード準備ツールを使用して、関数呼び出しと、コード生成でサポートされていないデータ型の使用を識別するレポートを作成します。

コード生成用のアルゴリズムを準備した後、Fixed-Point Designerを使用してコードをインストルメント化および高速化できます。 使用する

 buildInstrumentedMex 

すべての名前付き変数と中間変数の最小値と最大値を記録できるようにします。 また使用する

 showInstrumentationResults 

固定小数点で推奨されるデータ型を含むコード生成レポートを表示します。 走る

 fiaccel 

MATLABアルゴリズムをMEXファイルに変換し、固定点でのシミュレーションを高速化するため。

アルゴリズムコードで使用される関数の固定小数点サポートの確認

コード生成でサポートされていない関数を特定する場合、次の3つのオプションがあります。

1. 固定点で関数を同等の関数に置き換えます。
2. 独自の同等の関数を作成します。
3. 関数の入力でdoubleへの型キャストを使用してサポートされていない関数を分離し、出力で固定小数点への逆キャストを行います。

その後、コードを引き続き固定小数点に変換し、適切な置換がある場合はサポートされていない関数に戻ることができます（表2）。

元のコード	変更されたコード
y = 1/exp(x);	y = 1/exp(double(x));

表2.型キャストを使用して浮動小数点演算を分離する前後のコード（出力での固定小数点への逆キャストは表示されていません）。

データタイプ管理とビットレート制限
固定小数点の実装では、固定小数点の変数は、ビット深度が制限されたまま算術的であり、任意に浮動小数点になってはなりません。 ビット深度の上昇を防ぐことも重要です。

たとえば、次のコードを検討してください。

 y = y + x(n) 

この式はyを値で上書きします

  y + x(n) 

コードの固定ポイントでデータ型を使用する場合（yおよびxの場合）、データ型yは上書き後に変更される可能性があり、ビット深度が増加する可能性があります。

構文を使用してデータ型yを保存します

 (:) = 

（表3）。 インデックス割り当てと呼ばれるこの構文は、MATLABに既存のデータ型と書き換え可能な変数の配列サイズを保持するように強制します。 表現

 y(:) = y + x(n) 

右側の式を元のデータ型yに変換し、ビット深度の増加を防ぎます。

元のコード	変更されたコード
y = 0; for n=1:length(x) y = y + x(n); end	y = 0; for n=1:length(x) y(:) = y + x(n); end

表3.ビットの増加を防ぐためにインデックス割り当てを使用する前後のコード。

データ型定義とアルゴリズムコードを分離するための型を持つテーブルの作成
データ型定義とアルゴリズムコードを分離すると、固定ポイントで実装を比較し、アルゴリズムを他のターゲット機器に転送しやすくなります。

このベストプラクティスを適用するには、次の手順を実行します。

1. 使用する
   

    cast(x,'like',y) 

   または
   

    zeros(m,n,'like',y) 

   変数が最初に定義されたときに、変数の型を目的のデータ型にキャストします。
2. コードで使用される元のデータ型（通常は倍精度浮動小数点）から開始して、MATLABの既定のデータ型である型定義のテーブルを作成します（表4a）。
3. 固定小数点に変換する前に、単一のデータ型を型テーブルに追加して、不整合やその他の問題を検索します（表4b）。
4. 異なるデータ型を使用して各テーブルにバインドされたコードを実行し、結果を比較して、バインドを確認します。

元のコード	変更されたコード
% n = 128; y = zeros(size(x));	% T = mytypes('double'); n = cast(128,'like',Tn); y = zeros(size(x),'like',Ty); % function T = mytypes(dt) switch(dt) case 'double' Tn = double([]); Ty = double([]); end end

表4a。 データ型テーブルを作成する前後のコード。アルゴリズム定義コードを型定義から分離します。

元のコード	変更されたコード
% function T = mytypes(dt) switch(dt) case 'double' Tn = double([]); Ty = double([]); end end	% function T = mytypes(dt) switch(dt) case 'double' Tn = double([]); Ty = double([]); case 'single' Tn = single([]); Ty = single([]); end end

表4b。 型テーブルに単精度データ型を追加する前後のコード。

型テーブルの固定点にデータ型を追加する
データ型定義を含むテーブルを作成したら、固定小数点への変換の目標に基づいて、固定小数点でデータ型を追加できます。 たとえば、アルゴリズムをCで実装する場合、固定小数点のデータ型のワードサイズは16の倍数に制限されます。一方、HDLで実装する場合、ワードサイズは制限されません。

コードに推奨されるデータ型のセットを取得するには、Fixed-Point Designerコマンドを使用します

 buildInstrumentedMex 

そして

 showInstrumentationResults 

（表5）。 Fixed-Point Designerによって提案された型は優れたテスト効果と同じくらい優れているため、すべての型を使用する一連のテストベクトルが必要になります。 広範囲の予想される入力を使用した連続シミュレーションにより、提案された最高のデータ型が得られます。 コード生成レポート（図1）で提案されているものから、固定点の初期データセットを選択します。


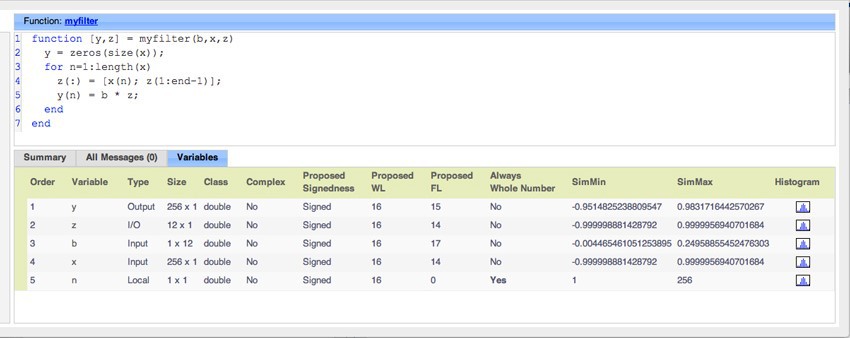
図1.フィルタリングアルゴリズムの変数に対して提案されたデータ型を使用してshowInstrumentationResultsによって生成されたコード生成レポート。

その後、必要に応じて、推奨されるタイプを微調整できます（表5および6）。

アルゴリズムコード	テストファイル
function [y,z] = myfilter(b,x,z) y = zeros(size(x)); for n=1:length(x) z(:) = [x(n); z(1:end-1)]; y(n) = b * z; end end	% b = fir1(11,0.25); t = linspace(0,10*pi,256)'; x = sin((pi/16)*t.^2); % z = zeros(size(b')); % buildInstrumentedMex myfilter ... -args {b,x,z} -histogram % [y,z] = myfilter_mex(b,x,z); % showInstrumentationResults myfilter_mex ... -defaultDT numerictype(1,16) -proposeFL

表5.コードのインストルメント化と実行、および変数の固定小数点での提案されたデータ型の表示のためのフィルタリングアルゴリズムとテストスクリプト。

アルゴリズムコード	テストファイル	タイプ表
function [y,z] = myfilter(b,x,z,T) y = zeros(size(x),'like',Ty); for n=1:length(x) z(:) = [x(n); z(1:end-1)]; y(n) = b * z; end end	% b = fir1(11,0.25); t = linspace(0,10*pi,256)'; x = sin((pi/16)*t.^2); % % T = mytypes('fixed16'); b = cast(b,'like',Tb); x = cast(x,'like',Tx); z = zeros(size(b'),'like',Tx); % [y,z] = myfilter(b,x,z,T);	function T = mytypes(dt) switch dt case 'double' Tb = double([]); Tx = double([]); Ty = double([]); case 'fixed16' Tb = fi([],true,16,15); Tx = fi([],true,16,15); Ty = fi([],true,16,14); end end

表6.固定小数点のデータ型を使用した、表4のテストスクリプトとフィルタリングアルゴリズム。

固定小数点で新しいデータ型を使用してアルゴリズムを実行し、出力を浮動小数点の参照アルゴリズムの結果と比較します。

データ型の最適化
固定小数点で独自のタイプを選択した場合でも、提案されたFixed-Point Designerを使用した場合でも、ワードサイズ、小数部のサイズ、文字、場合によっては算術モード（ fimath ）を最適化する機会を常に探してください。 これは、スケーリングされたdoubleを使用して、変数値のヒストグラムを調べるか、タイプテーブルの異なるデータタイプをテストすることで実行できます。

スケーリングされたdoubleを使用して潜在的なオーバーフローを検出する
スケーリングされたdoubleは、浮動小数点数と固定小数点数のハイブリッドです。 Fixed-Point Designerは、スケーリングされたdoubleを倍精度の数値として格納しますが、ビット深度、符号、語長に関する情報を格納します。 スケーリングされたdoubleを使用するには、データ型オーバーライド（DTO）プロパティを設定する必要があります（表7）。

DTOをインストールする	例
DTOは次を使用してローカルにインストールされます numerictype プロパティ 'DataType'	>> Ta = fi([], 1, 16, 13, 'DataType', 'ScaledDouble'); >> a = cast(pi, 'like', Ta) a = 3.1416 DataTypeMode: Scaled double: binary point scaling Signedness: Signed WordLength: 16 FractionLength: 13
DTOは次を使用してグローバルにインストールされます fipref プロパティ 'DataTypeOverride'	>> fipref('DataTypeOverride', 'ScaledDoubles'); >> Ta = fi([], 1, 16, 13); >> a = cast(pi, 'like', Ta) a = 3.1416 DataTypeMode: Scaled double: binary point scaling Signedness: Signed WordLength: 16 FractionLength: 13

表7.データ型を上書きするプロパティを設定する方法-ローカルおよびグローバル。

コマンドで不要になった場合は、グローバルDTOをリセットすることを忘れないでください

 reset(fipref) 

buildInstrumentedMexを使用してコードを実行し、showInstrumentationResultsを使用して結果を表示します。 コード生成に関するレポートでは、オーバーフローする値は赤で強調表示されます（図2）。


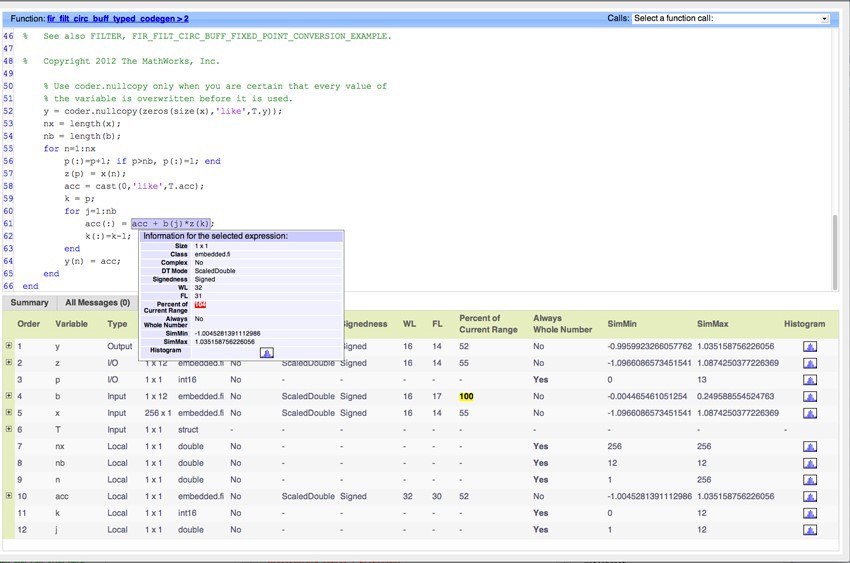
図2. Scaled Doublesタイプ（左）とヒストグラムアイコン（右）を使用した場合のオーバーフローを示すコード生成レポート

変数値の分布を確認する
ヒストグラムを使用して、許容範囲内、範囲外、または解像度（精度）未満の値を持つデータ型を識別できます。 ヒストグラムアイコンをクリックすると、 NumericTypeScopeを実行して、選択した変数のシミュレーション中に観測された値の分布を確認できます（図3）。


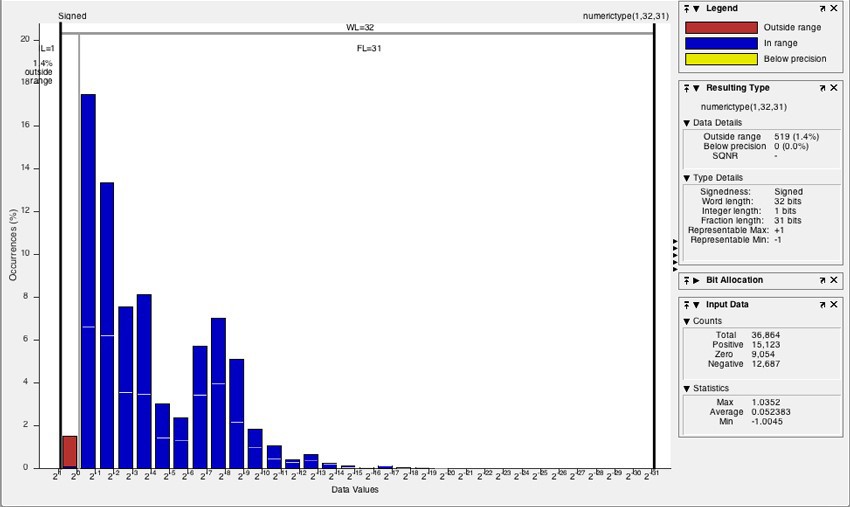
図3.オーバーフローした変数の値の分布を示すヒストグラム（「範囲外」）、赤で表示

タイプテーブルからのさまざまなタイプのデータのテスト
データ型の独自のバリエーションをタイプテーブルの固定ポイントに追加できます（表8）。

アルゴリズムコード	テストファイル	タイプ表
function [y,z] = myfilter(b,x,z,T) y = zeros(size(x),'like',Ty); for n=1:length(x) z(:) = [x(n); z(1:end-1)]; y(n) = b * z; end end	function mytest % b = fir1(11,0.25); t = linspace(0,10*pi,256)'; x = sin((pi/16)*t.^2); % % y0 = entrypoint('double',b,x); y8 = entrypoint('fixed8',b,x); y16 = entrypoint('fixed16',b,x); % subplot(3,1,1);plot(t,x,'c',t,y0,'k'); legend('',' ') title(' ') subplot(3,2,3);plot(t,y8,'k'); title('8- . : ') subplot(3,2,4);plot(t,y0-double(y8),'r'); title('8- . : ') subplot(3,2,5);plot(t,y16,'k'); title('16- . : ') xlabel(' ()') subplot(3,2,6);plot(t,y0-double(y16),'r'); title('16- . : ') xlabel(' ()') end function [y,z] = entrypoint(dt,b,x) T = mytypes(dt); b = cast(b,'like',Tb); x = cast(x,'like',Tx); z = zeros(size(b'),'like',Tx); [y,z] = myfilter(b,x,z,T); end	function T = mytypes(dt) switch dt case 'double' Tb = double([]); Tx = double([]); Ty = double([]); case 'fixed8' Tb = fi([],true,8,7); Tx = fi([],true,8,7); Ty = fi([],true,8,6); case 'fixed16' Tb = fi([],true,16,15); Tx = fi([],true,16,15); Ty = fi([],true,16,14); end end

表8.フィルター関数のタイプテーブルから固定ポイントでさまざまなデータタイプを使用した場合の効果を調べるためのテストスクリプト。

異なる反復の結果を比較して、各変更後のアルゴリズムの精度を検証します（図4）。


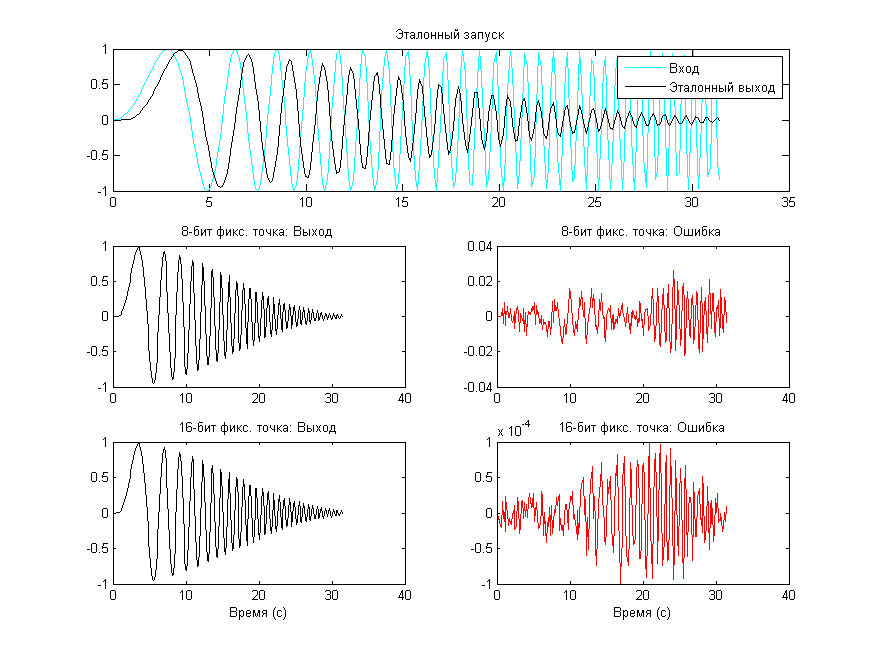
図4.表8のテストスクリプトの結果のグラフ。固定小数点で8ビットおよび16ビットのデータ型に変換した後の出力とエラーを示しています。

アルゴリズムの最適化

アルゴリズムを最適化してパフォーマンスを改善し、より効率的なCコードを生成するには、3つの一般的な方法があります。
次のことができます。

• fimathプロパティを使用して、生成されたコードの効率を改善する
• インライン関数をより効率的な固定小数点実装に置き換えます
• 他の方法で除算操作を実装する

fimathプロパティを使用して生成されたコードの効率を改善する

デフォルトのfimath設定を使用すると、追加のコードを生成して、オーバーフロー、丸め、算術中の飽和を完全な精度で実装できます（表9a）。

MATLABコード	生成されたCコード
: function y = adder(a,b) y = a + b; end , fimath : Ta = fi([],1,16,0); Tb = fi([],1,16,0); a = cast(0,'like',Ta); b = cast(0,'like',Tb);	int adder(short a, short b) { int y; int i0; int i1; int i2; int i3; i0 = a; i1 = b; if ((i0 & 65536) != 0) { i2 = i0 | -65536; } else { i2 = i0 & 65535; } if ((i1 & 65536) != 0) { i3 = i1 | -65536; } else { i3 = i1 & 65535; } i0 = i2 + i3; if ((i0 & 65536) != 0) { y = i0 | -65536; } else { y = i0 & 65535; } return y; }

表9a。 デフォルトのfimath設定で生成された元のMATLABコードとCコード。

生成されたコードをより効率的にするには、プロセッサタイプに合った固定小数点演算設定を選択する必要があります。 fimathプロパティを使用して算術、丸め方法、およびオーバーフローアクションを記述し、fiオブジェクトで算術演算を実行するためのルールを設定します（表9b）。

MATLABコード	生成されたCコード
: function y = adder(a,b) y = a + b; end , fimath : Ta = fi([],1,16,0); Tb = fi([],1,16,0); a = cast(0,'like',Ta); b = cast(0,'like',Tb);	int adder(short a, short b) { return a + b; }

表9b。 プロセッサの種類に適したfimath設定で生成された元のMATLABコードとCコード。

インライン関数を固定小数点実装で置き換える
一部のMATLAB関数は、固定小数点でより効率的な実装を取得するために置き換えることができます。 たとえば、組み込み関数を、反復シフトおよび合計演算のみを必要とする補間テーブルまたはCORDIC実装に置き換えることができます。

他の方法での除算操作の実装
多くの場合、除算演算はハードウェアによって完全にサポートされておらず、計算が遅くなる可能性があります。 アルゴリズムに除算演算が必要な場合は、より高速な代替演算に置き換えることを検討してください。 分母が2のべき乗の場合、ビットシフトを使用します。 たとえば、x / 8の代わりにbitsra（x、3）を使用します。 分母が定数の場合、逆数を掛けます。 たとえば、x / 5の代わりにx * 0.2を使用します。

次は？
Fixed-Point Designerを使用して説明したベストプラクティスを使用して浮動小数点コードを固定小数点に変換した後、現実的なテスト入力を使用して固定小数点実装を徹底的にテストし、シミュレーション結果を浮動小数点リファレンスのビットと比較します。