アルベロス

記事をMathematica（NB）ドキュメント 、 CDFファイル、またはPDFとしてダウンロードします 。
翻訳に協力してくれたキリル・グゼンコに深く感謝します。

---

この記事では、 アルベロスと呼ばれる古代から知られている人物の特性のいくつかを体系的にチェックします。 この作品の著者によって提示されたいくつかの新しい発見と一般化が含まれています。

はじめに

Mathematicaが持つ計算上の利点に動機付けられて、しばらく前に、非常に興味深い幾何学図形であるアルベロスの特性の研究を開始することにしました。 それ以来、私はこの注目すべき物体に関する膨大な数の文献のために生じた驚くべき発見と計算上の問題の多くに感銘を受けました。 The Prisoner（1960年代のテレビシリーズ）のカルトペニーファーシングバイクの底、有名なPunch and Judyのパンチキャップ、および1つの逆円弧の陰陽のシンボルに似ていることを思い出します。 写真を見て 1.現在、アルキメデスの円（アルベロスに含まれる円）の専門カタログ[1]と、数学と計算科学の分野外にあるアルベロス特性の重要なアプリケーションがあります[2]。

アルキメデス（紀元前212年にローマの兵士によって殺された）、パップ（紀元前320）、クリ​​スチャンO.モア（1835-1918）、ビクターテボ（ 1882-1960）、レオンバンクオフ（1908-1997）、マーティンガードナー（1914-2010）。 最近、クレイトンドッジ、ピーターエイはアルベロスの特性を扱っています。 呉、トーマス・ショー、奥村博、渡辺雅之など。

レオン・バンクフは、過去30年間に誰もがアルベロスに注目した男です。 ショッホは1979年にバンクフの注目をアルベロスに引き付け、いくつかの新しいアルキメデスのサークルを開きました。 彼は20ページの原稿をMartin Gardnerに送り、Martin GardnerはそれをBankoffに送り、それから1996年にDodge原稿のコピーの10ページの断片を送りました。 Bankoffの死により、Dodgeがいくつかの新しい発見を発表するまで、計画されていたコラボレーションは中断されました[3]。 1999年に、ドッジは、彼が持っていたすべての材料を整理し、すべてを山に入れて5〜10年かかると言いました。 この作業はまだ進行中です。 驚くことではないが、 The Art of Computer Programmingの第4巻では、重要な作業には多くの時間が必要であると述べています。


図 1. 自転車のペニーファージング、人形のパンチとジュディ、物理的なアルベロス。

アルベロス（ギリシャ語で「靴屋のナイフ」）は、靴屋が使用するナイフの刃に似ていることから命名されました（図1）。 アルベロスは、3つの半円と共通のベースラインに囲まれた平坦な領域です（図2）。 アルキメデスは恐らくアルベロスの数学的特性を研究し始めた最初の人でした。 これらの特性は、彼の本Liber assumptorum （またはLemmasの本 ）の4から8の定理に記述されています。 おそらくこの作品はアルキメデスによって書かれたのではないでしょう。 疑念は、アルキメデスが繰り返し言及されたアラビア語のLemmasの本の翻訳の後に生じたが、彼の著者については何も言われなかった（しかし、この本は偽物であるという意見がある[4]）。 レムの本には、有名なアルキメデスのボボナムの問題も含まれています [5]。

この記事は、アルベロスのいくつかの特性を体系的に提示することを目的としており、網羅的ではありません。 私たちの目標は、これらのプロパティをトレーニング記事の形式で提示するための統一された計算方法論を開発することです。 すべてのプロパティは特定の順序で配置され、証拠とともに提示されます。 この証拠は、同等の計算されたステートメントをテストすることで実現されました。 この作業の過程で、著者はいくつかの発見を行い、いくつかの一般化を行いました。

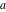
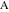
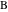
最大の半円を上部の円弧 、2つの小さな半円- 左側の 円弧と右側の円弧 、または単に区別する必要がない場合は単に側面の円弧と呼びます。 使用します そして それぞれ、それらの半径を示し、上部の弧の半径は 。 2つのポイント間の線は方向付けられておらず、あるポイントから別のポイントまで伸びていますが、2つのポイントを含む直線は無限で、これらの2つのポイントの外側にあります。 表記の古典的な不正確さ-使用 ポイントを接続するセグメント自体として指定する そして 、およびコンテキストに応じたその長さ。 現代の表記法は、書くように指示します セグメントの長さを示します。

この関数は、アルベロスを設定します。



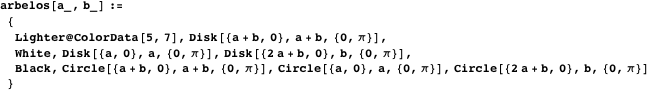
だから、アルベロス自体を描くことができます。




図2. アルベロス。

物件1
アルベロスの周囲は最大の円の周囲に等しい。

物件2
アルベロスの面積は直径のある円の面積に等しい 。

これは、補題帳の補題4です（図3）[7、8]。

これらの2つの特性は、2つの等式で構成される以下に示す論理構造を計算することで簡単に証明できます。





drawpoints関数は、指定されたポイントを赤丸で表示します。






図 3. 直径の円の面積 （ラジカル円）はアルベロスの面積に等しい。

ラジカルサークル

ご飯の輪。 3はアルベロスの過激なサークルと呼ばれ、 ラジカル軸と呼ばれます （この用語は一般化で説明されます）。 プロパティ3-11および25-26を説明するために必要なポイント、ライン、円、座標を指定して名前を変更します（図4）。




図 4. プロパティ3-11および25-26に記載されている座標、線、および円の指定。

物件3
行 そして 垂直であり、点で横弧を横切る そして 側面のアーチに共通の接線で接続します。

線の垂直性を証明する そして 、ベクトルのスカラー積を計算します そして 。





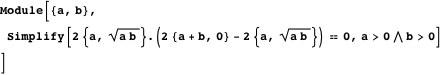
結果を使用して、線の勾配を取得します 。

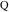
定理1
での左弧への接線の方程式 ：



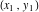
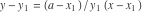
そして、右弧への接線の方程式 ：



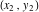
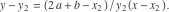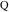
PQ関数はタッチポイントの座標を見つけます そして 定理1に従って、円弧上の位置と接線の傾斜角を指定する4つの方程式系を解くことにより、

この記事には、 PQに加えて、ポイントと数量の表記法VWS 、 HK 、 U 、 EF 、 IJr 、 LMも含まれています。

dSq関数は、与えられた2点間の距離の2乗を計算します。









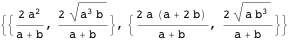プロパティ4
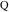
ポイント そして 過激なサークルにいます。

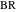
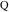
以来 はラジカルの円の直径であり、距離の等式を証明するだけでよい そして として定義されているラジカル円の中心に 。





物件5
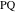
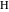
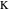
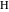
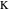
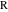
行こう 点で上の弧を横切る そして 。 それから そして を中心とする円の上に横たわる および半径 。

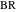
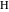
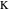
ポイントの座標を取得します そして 、上の弧と線上の位置を定義する方程式系を解く 。







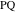
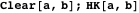
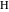
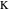
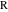
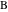
これは、距離5 そして 前に からの距離に等しい 前に 。





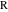
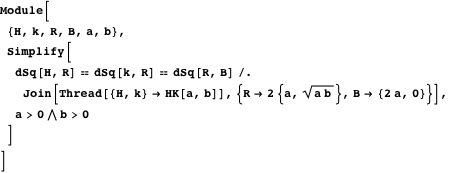
物件6
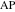
直接 まっすぐに平行 。

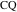
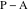
これはベクトル行列式と同等です そして （それらのベクトル積）はゼロです。





物件7
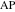
直接 線に垂直 。

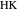
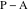
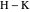
これは、ベクトルのスカラー積と同等です そして ゼロに等しい。





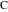
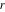
中心にある円を示します および半径 どうやって 。

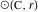
物件8
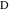
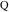
カップル 、 そして 、 -円の相互に逆の点のペアを表す 。

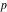
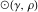
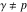
ポイントツーポイント 周り （同時に ）そのような点です その平等が成り立つ [9]。 反転関数はこの考えを実装しています。



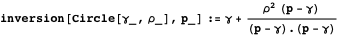
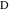
したがって、プロパティ8は、 の代わりに 。





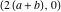
物件9
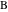
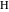
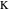
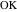
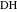
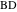
リターンポイントの円を探索する 。 与えられた点の円に対して 、 、 戻り点と一致します。 線分 アークの逆です 、およびセグメント -アーク反転 。 アーク そして また、相互に逆です。 過激な円は線の逆です 。

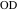
物件10
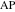
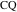
直接 そして ラジカル円に接線があります。

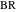
このステートメントは、対応する円弧（つまり、それらの接線）がラジカル円（交差点での接線）に垂直であるという事実に似ています。 プロパティ8によると、円弧は直径のある円に垂直です リターンポイントのペアを通過する場合[10,11]。

物件11
-長方形。

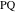
これは、Bankoffの驚きの1つです[12,13,14]。 4つのポイントすべてが過激な円上にある場合、それを証明するだけで十分です。 二分 。





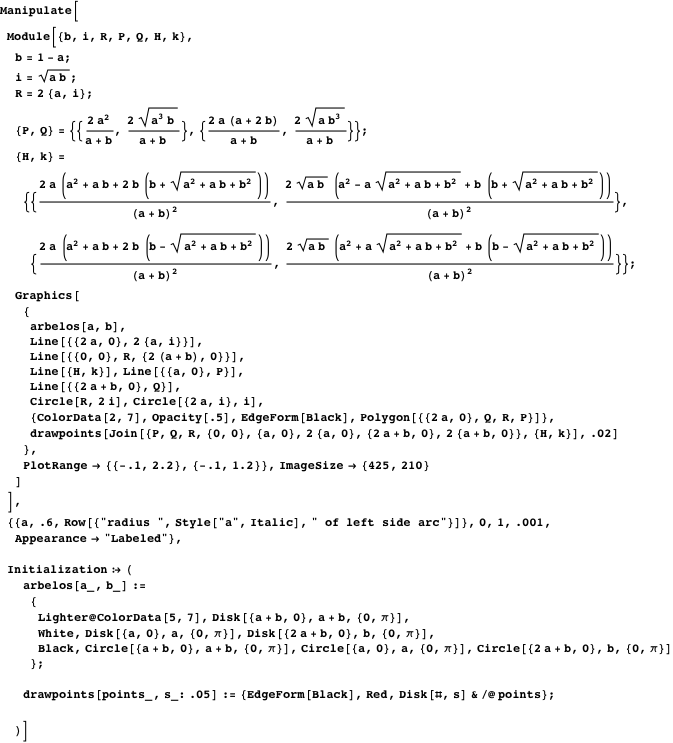
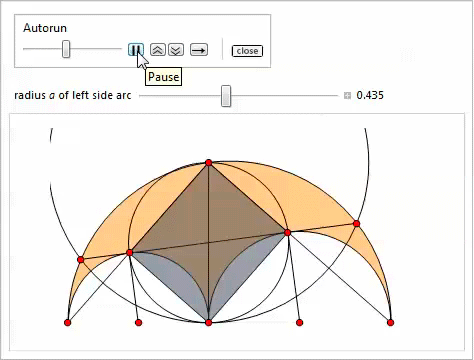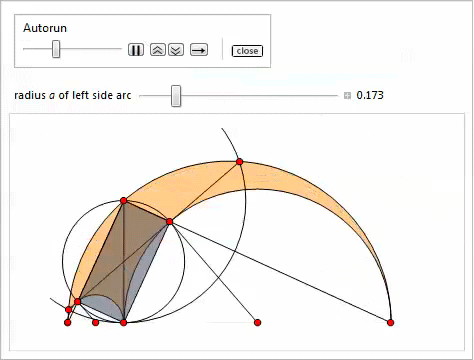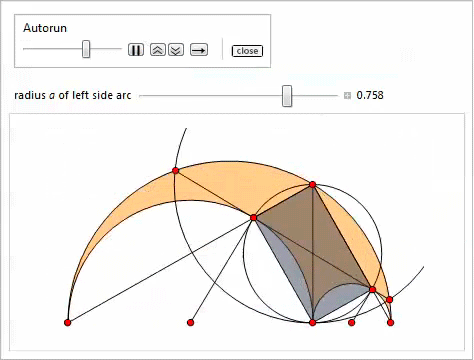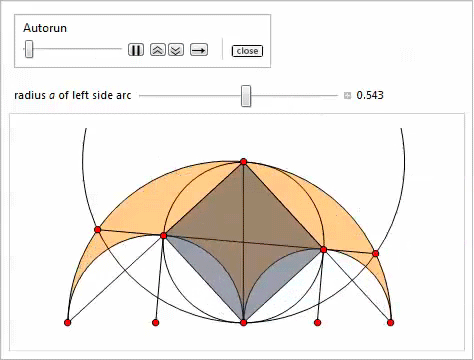
スライダーを使用した次のデモ（ 操作関数を使用して実装）は、プロパティ3〜11を示しています。 ポイントP 、 Q 、 H 、 Kを指定する最も簡単な方法は、それらに対応する数式をコピーして貼り付けることです。

内接円

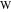
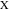
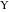
次に、側面円弧と上部円弧に接する円を考えます- 内接円 タッチポイント付きのアルベロス 、 、そして （図5を参照）[15、16]。 また、アークの頂点をドットで示します そして それに応じて。




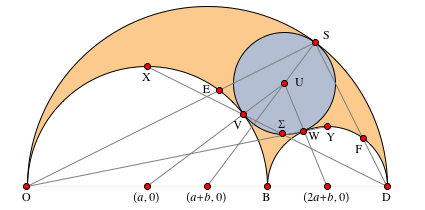図 5. 内接円 、図に示されている座標、線、点はプロパティ12〜15に表示されます。

補綴書の6番目の文には、次のように表記される内接円の半径も含まれています。 。 関数u 中心座標を計算します 内接円とその半径 。







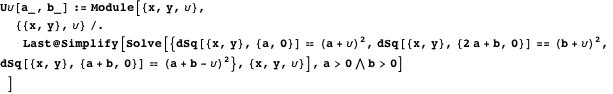
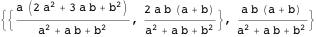
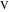
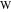
タッチポイント座標 、 、そして アルベロス弧の中心と内接円を結ぶ線の交点によって決定されます。







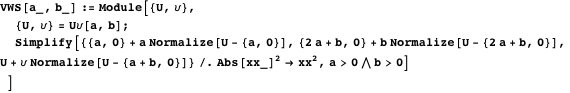
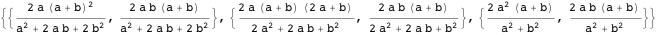物件12
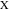
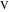
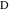
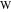
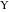
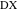
ポイント 、 、そして 一直線上にあります。 ポイント 、 、そして 一直線上にあります。 行 そして 点で交差する 内接円上にあります。

最初の2つのステートメントは、共線性を検証するための行列式基準を使用して証明できます。





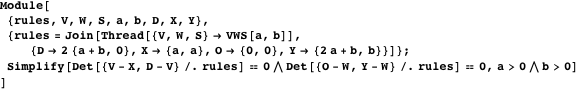
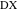
させる 線の交点になります そして 。 この点からの距離が 等しい 、3番目のステートメントを証明します。





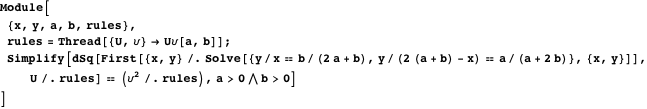
物件13
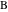
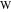
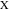
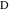
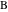
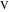
ポイント 、 、 、そして 中心にある円の上に横たわる 。 同様に、ポイント 、 、 、そして 中心にある円の上に横たわる 。









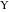
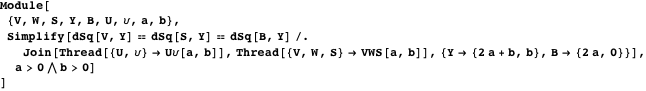
Manipulateを使用した次のデモは、プロパティ13 [17]を示しています。 [ バンクオフ円 ]オプションでは、円弧の中心を結ぶ三角形に内接円が表示されます。 これはプロパティ23を示しています。





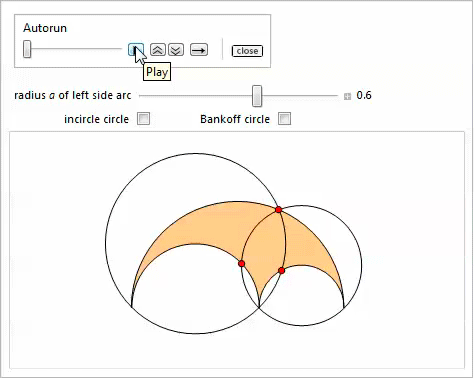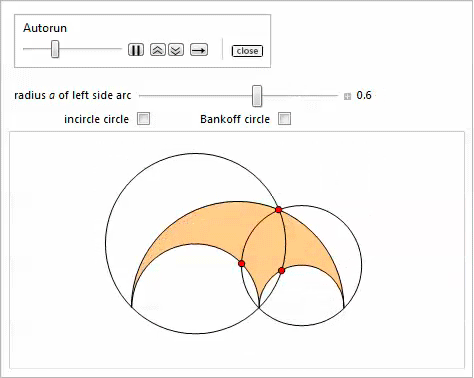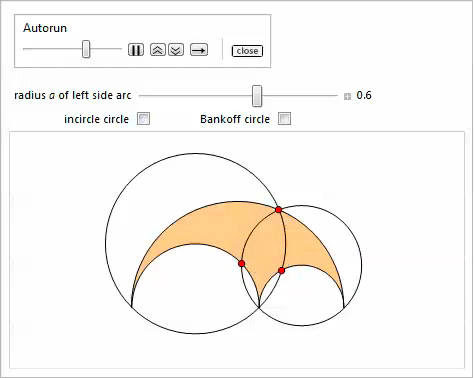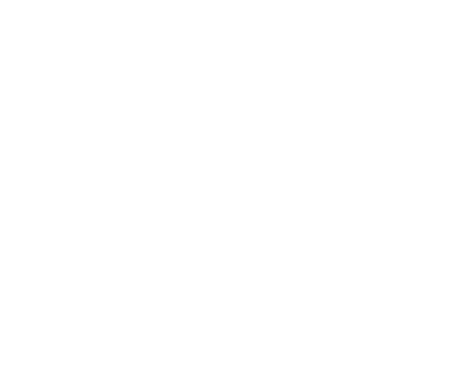物件14
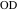
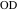
させる -内接円の直径、平行 、そして -投影 に 。 線分間の長方形 そして -正方形。

このプロパティは、次のManipulateのデモで説明されており、次の式で簡単に検証できます。





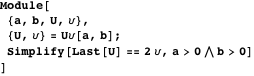
物件15
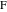
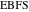
させる そして -線の交点 そして サイドアーチ付き。 それから -正方形は、プロパティ14に記載されている正方形とほぼ同じサイズです。

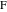
まず、ポイントを取得します そして 対応する線と円弧の交点として、結果をreplaceEF変数に保存します。







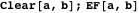
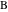
資産15を証明する 回転によって得られたベクトルに等しい 周り 90°と作り 変位によって得られたベクトルに等しい を通して 。





検討中 そして 次のグラフは、2つの正方形のサイズを比較しています。





Manipulateを使用したデモでは、プロパティ14と15を示しています。

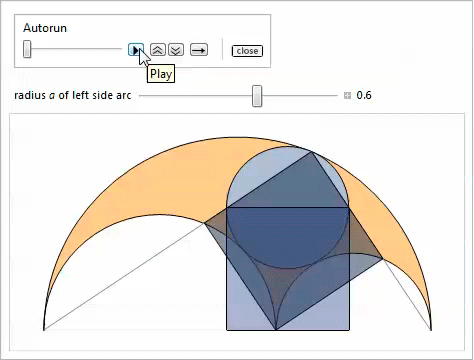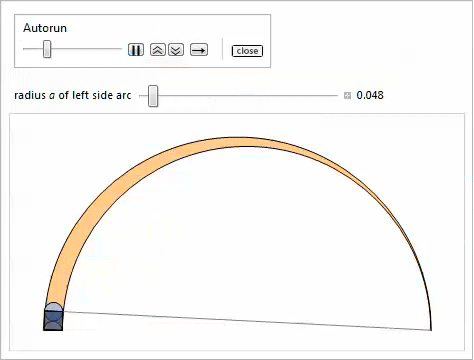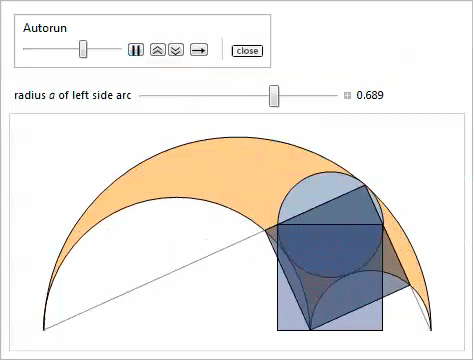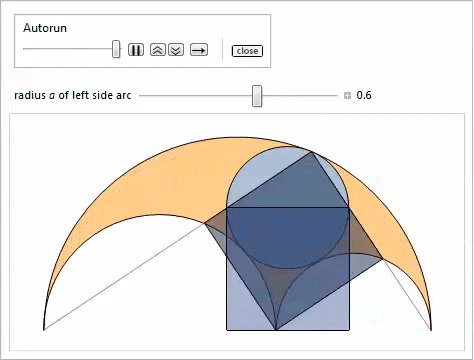
双子

ラジカル軸に接する2つの灰色の円と、図の横方向および上方向の円弧を考えてみましょう。 6.それらは双子 、またはアルキメデスの円と呼ばれます。 次の注目すべき特性に関連して、それらはよく研究されています。 それらの異常な機能の多くは、プロパティのリストで強調されています[3、18、19]。




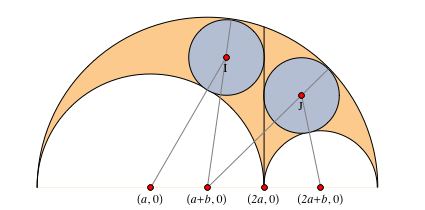図 6. 双子。

物件16
ラジカル軸に接する2つの円、Arbelosの上部と側面のアーチは同じ半径を持っています。

このプロパティは、レンマ書の 5番目のステートメントとして使用されます。 この6つの方程式のシステムを解いて、半径の値を見つけ、それらが等しいことを確認し、それらの中心の座標を見つけます 、 。





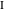
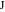
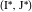
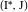
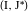
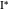
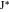
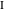
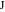
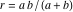
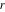
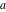
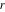
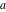
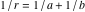
これらの4つのソリューションは、センターをペアでグループ化します。 、 、 、 どこで そして マッピングです そして アルベロスの直径; 最後の式のみが有効です。 また、双子が実際に同じ半径であることも示しています 。 半径が双子と同じ長さの円は、 アルキメデスと呼ばれます。 あなたはかなり明確な類推を描くことができます 想像したら そして -（電気）抵抗。 それから -並列接続によって得られる抵抗 そして ; それは 。 IJr関数は、中心の座標と双子の半径の長さを計算します。



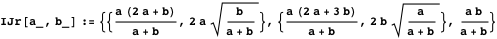物件17
アルベロスの面積は、双子にまたがる最小の円の面積に等しくなります。

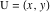
を中心とする両方の双子に接する円を考えます および半径 。 次に、次の2つの値があります。 。







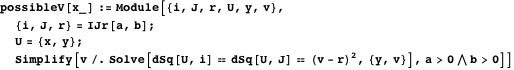
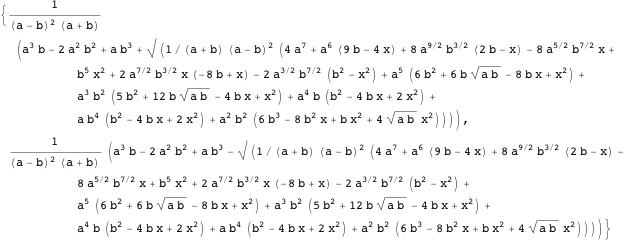
の極値を見つけるには 、両方の方程式の導関数をゼロに等しくし、 。





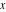
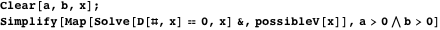
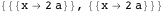
したがって、双子に接する最小および最大の円の中心は、ラジカル軸上にあります。 さらに、それらの中心は、この表現の解から導かれる1つのポイントにあります。





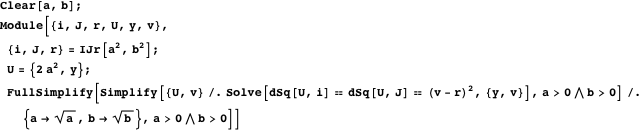
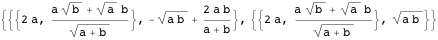
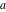
したがって、プロパティ2を使用すると、双子を含む円の中で最も小さい最大の接線円がプロパティ17を満たすことを証明します。次のManipulateのデモでは、双子に接する円を示します。 左側のアーチ。





次のグラフは、双子に接する2つの円の半径を、ラジカル軸上の中心と比較しています。








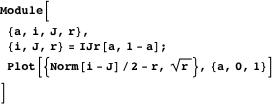
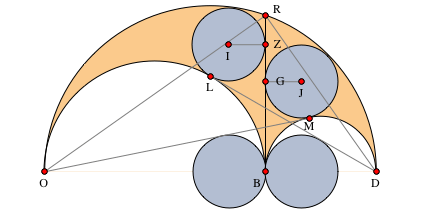図 7. プロパティ18〜24に表示されるポイントとセグメントの指定。

物件18
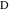
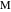
左アークと双子への一般的な接線（接触点- ）ポイントを通過する 。 同様に、右弧と双対の共通接線（接線の点- ）ポイントを通過する （図7を参照）。

タッチポイントを計算できます そして 。







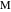
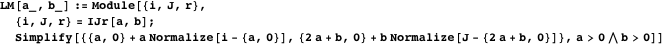
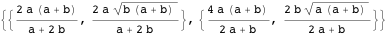
定理1を使用して、両方のステートメントを証明します。





物件19
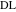
長さ 長さに等しい 。 長さ 長さに等しい 。

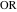
両方のステートメントを同時に証明します。





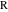
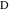
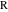
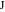
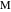
しかし、ポイント 、 、そして を中心とする円の上に横たわらないでください 、およびポイント 、 、そして を中心とする円の上に横たわらないでください ; そうでない場合、次の式はゼロになります。





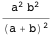物件20
行 行を分割します 半分に。 行 行を分割します 半分に。

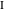
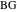
セグメントの長さ -縦座標 、およびセグメントの長さ -縦座標 、傾斜角を確認して、これらのセグメントの中心が指定された線上にあることを確認するだけで十分です。





物件21
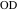
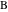
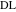
直径がオンの2つの青い円 通り抜ける および接線 そして アルキメデスです。

これらの円は、バンクフによって発見された4番目と5番目のアルキメデスの円です[20]。 このプロパティを確認するには、次の結果[21]を使用します。

定理2
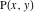
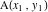
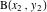
ポイントからの距離 点を通る線に そして あります：



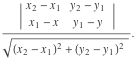
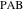
この向きの距離は、三角形が正の場合 反時計回りに交差し、それ以外の場合は負に交差します。 このマッピングは、 dAB関数を実装します。



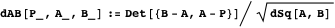
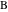
させる そして -それぞれ、ポイントの左側にある青い円の中心と半径 （図7）。 次のシステムを解くと、価値が見つかります 。





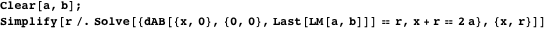
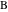
同様に、右の青い円の半径を計算できます 等しい 。





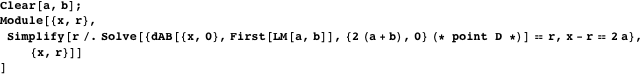
したがって、前述のように、両方の円はアルキメデスです。 Manipulateを使用した次のデモには、双子と2つの他の円が含まれています。





物件22
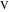
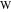
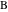
点を通る円 、 、そして 図 5、これはバンクオフ円と呼ばれ、アルキメデス円です。

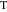
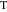
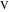
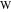
アルキメデスは元の双子を発見しました。 バンクオフは、1950年に発見された3番目の円で彼らを補った[22]。 中心座標 バンクオフ円は、からの距離を計算することで取得できます ポイントへ 、 、そして 。





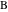
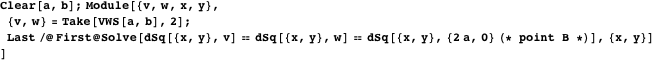
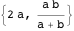物件23
バンクオフサークル-サイドアーチの中心とセンターの接続によって形成される三角形に内接 アルベロスに刻まれた円。

定理2を使用してからの距離を計算する 三角形の辺に対して、このプロパティを証明します（ dABは方向付けられた距離を計算するため、線を記述する引数の順序は非常に重要です）。





物件24
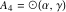
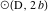
円周 円の接線 、 と上部の弧-アルキメデス。

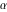
この方法で値を計算できます そして 。





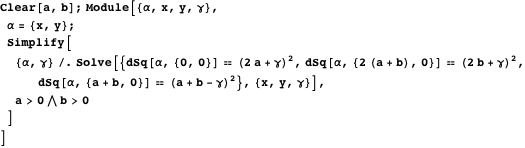
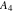
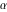
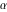
円周 -縦座標の唯一のもの -ポジティブ。 それに注意する必要があります -急進的な軸ではありません。





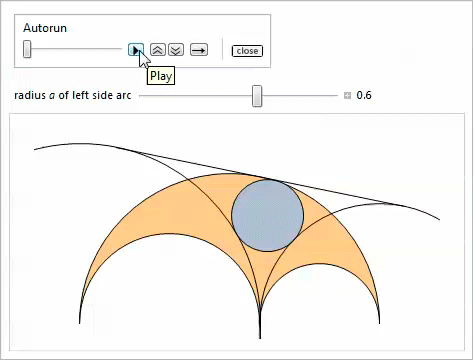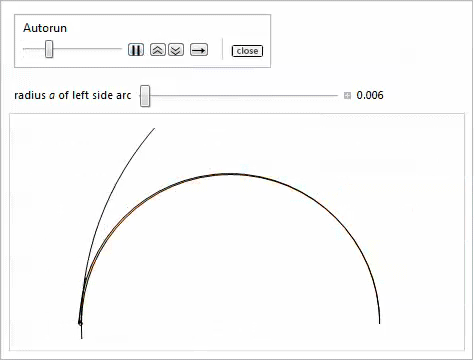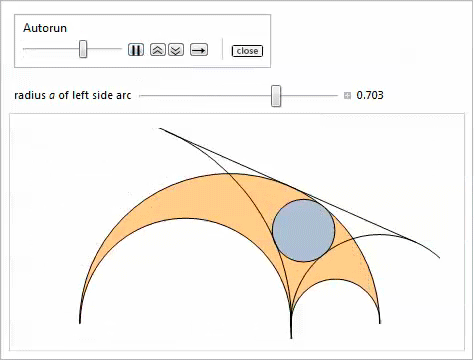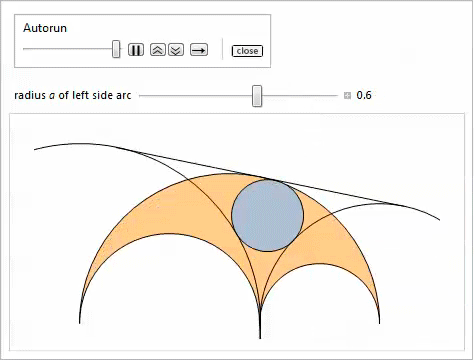物件25
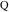
サークル そして ラジカル軸の接線と通過 そして したがって、それらはアルキメデスです（図4を参照）。





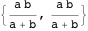物件26

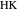
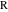
円周 線の接線 そして点の上の弧 -アルキメデス（図4参照）。

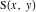
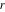
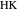
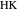
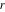
点を中心とした円 および半径 接線 などの距離 前に 等しい 、および方程式は次の形式を取ります。



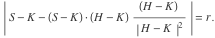
円が通るので 、



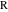
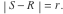
円以来 上部アークの接線、



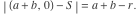
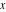
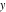
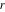
ここでは、明示的な式を使用して 、 、そして これらの3つの平等を満たします。





物件27
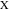
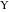
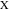
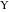
上部の円弧の中心と左の頂点を接続する2つのセグメント（赤でマーク）を検討します そして右 アルベロスアーク。 これらのセグメントは等しく、垂直です。 接線円 そして ポイントで そして これらのセグメントと上部アルキメデス弧に（図8を参照）。

このプロパティは、1998年の夏に発見されました[23]。




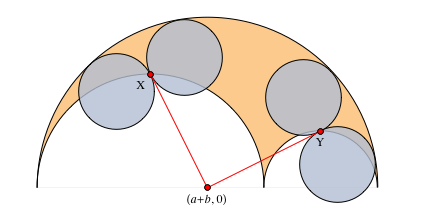図 8. プロパティ27からの2組のアルキメデス円。

傾斜双子

双子とは異なるアルキメデスの円、つまりバンクオフ円がプロパティ21-27に表示されることが示されました。 非アルキメデス双子もあります-アルベロスの特定の領域に現れる双子の半径とは異なる、同じ半径の円のペア。

傾斜双子の発見は、双子の円が外側および上部の円弧に触れることに加えて、互いに触れることができ、ラジカル軸に触れる必要がないという仮定から生じました。

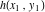
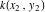
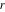
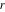
これらの円が同じ半径である必要がない場合、明らかに無限の数の解があります。 アイデアはこれでした：それらが等しい半径であるという仮定から始めると、最終的にそれらがラジカル軸に触れていることがわかります。 これは間違っていることが判明しました。 ポイントに中心がある円を考える そして そして同じ半径で 。 価値 5つの方程式からなるシステムを解くことで得られます。





これらの式には、符号が異なる平方根が含まれます。 ポジティブルーツは分岐します 逸脱します。





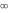
残りは収束します。





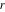
要約すると、斜めの双子は本当に等しく、それらの合計半径 等しい



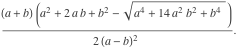
次の普通の双子と斜めの双子の半径の比較は、それらが非常にわずかに異なることを示しています。





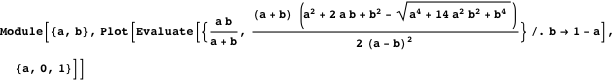
そのため、傾斜双子の中心の座標を取得できます。







以下のManipulateデモは、斜めの双子と、オプションでパラメーターを変更した結果の双子を示しています。 。

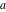
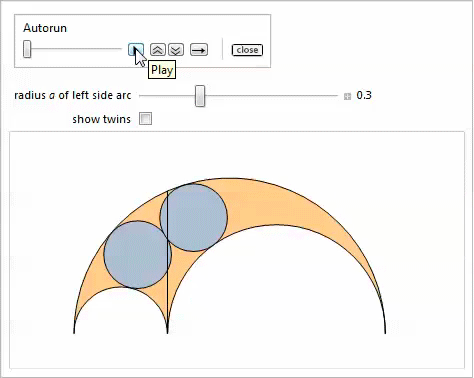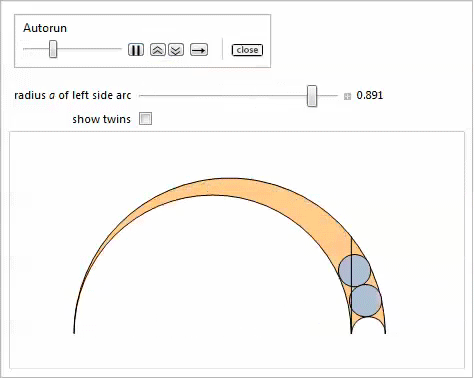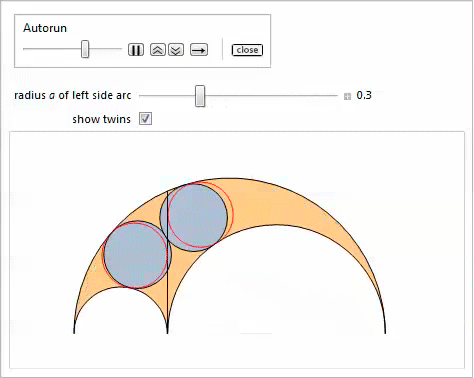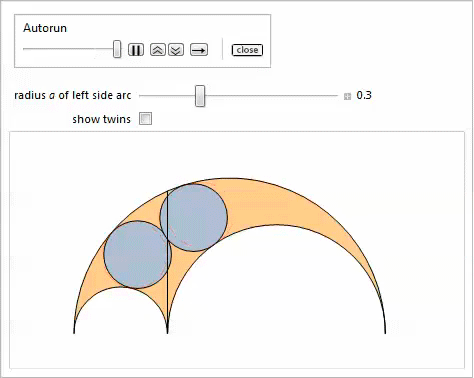
汎化

このセクションでは、アルベロスのジオメトリを一般化し、アークを交差させ、3次元バージョンを検討します。最初の一般化のコンテキストを定義するために、2つの円のラジカル軸の概念を導入します。

ラジカル軸

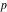
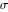
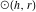
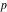
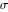
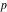
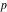
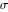
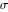
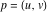
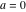
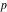
させる -ポイント、および -サークル 。 態度の程度 に ブロードキャスト番号によって決定 。 程度 ポジショニング、ゼロまたはネガティブ 外、上または内 、それぞれ[12]。 させる ; ポイントが属する場合 方程式を満たす その後、次数を決定できます コンピューティングにより 。 同じことが得られる場合 円が直線に縮退する場合、その場合は記号 どこを示します それは比較的まっすぐです：その上、その上、またはその下にそれぞれ。

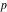
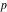
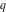
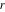
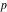
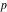
これは、ポイントの次数の非常に興味深い特性です。 円といくつかの点を与えてみましょう 。 通過する任意の行を選択します 点で交差する円 そして 。 その後、製品 のみに依存します 通過する線の選択に依存しません 。 この仕事は学位に等しい 。

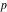
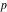
以下のManipulateのデモでは、円周、位置のサイズを変更するための4つのロケーターがあります。 線を傾けます 。





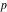
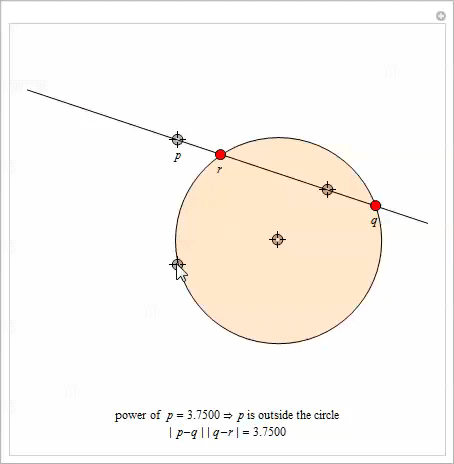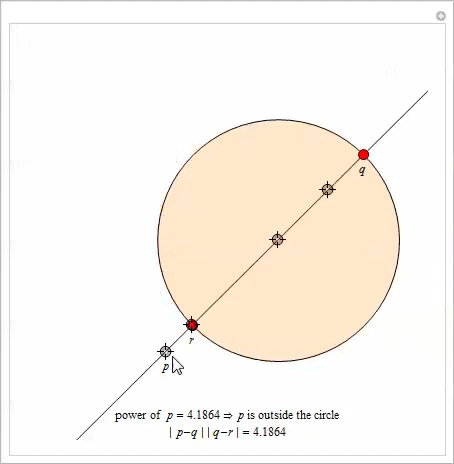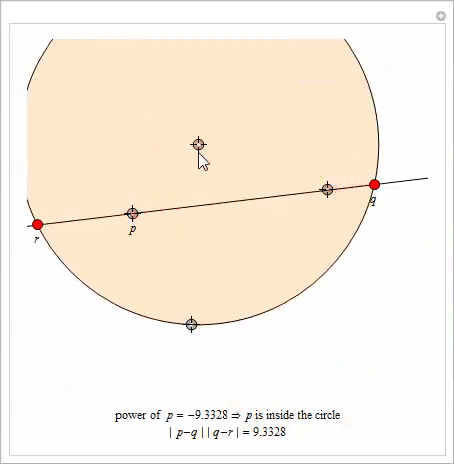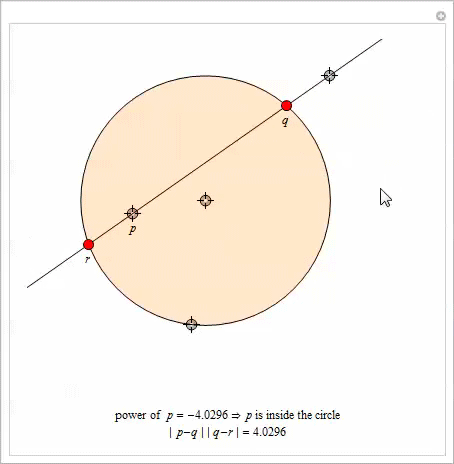
異なる点に中心を持つ2つの円を指定します。 それらのラジカル軸は 、各円に関して同じ次数を持つすべてのポイントを含む直線として定義されます。 この声明の証拠は[10]にあります。

定理3
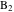
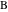
2つの円が点で交差する場合 そして その過激な軸は共通の割線です 。 2つの円が接触する場合 その場合、それらのラジカル軸は、 。

結果1
中心が同じ線上にない3つの円を指定します。 その場合、それらのラジカル軸はペアワイズ平行になり、一致しません。

定理4
2つの円の基軸は、それらに描かれた接線が同じ長さを持つ点の軌跡です。

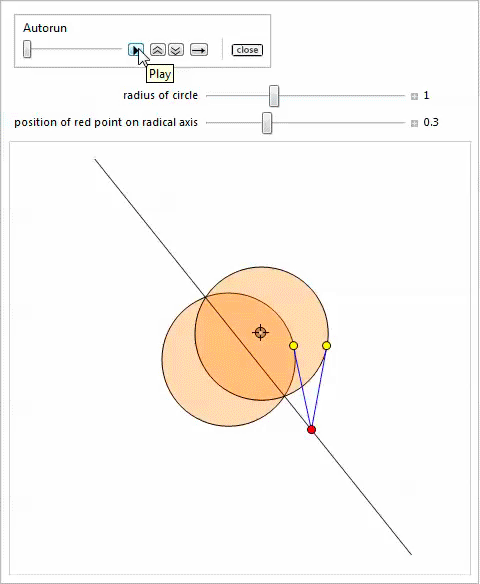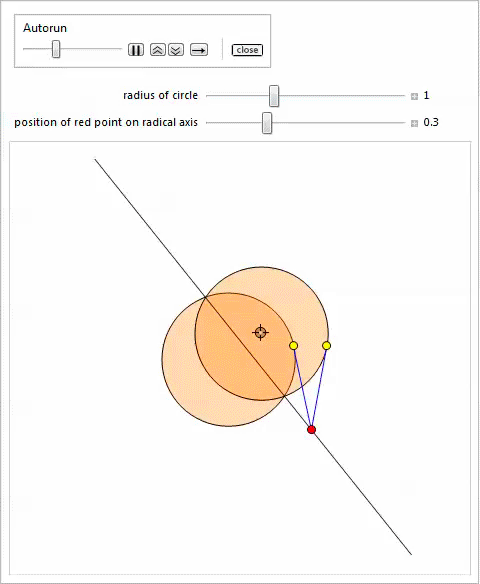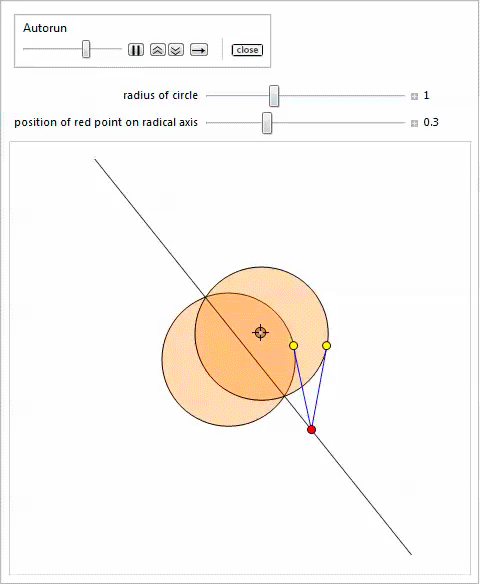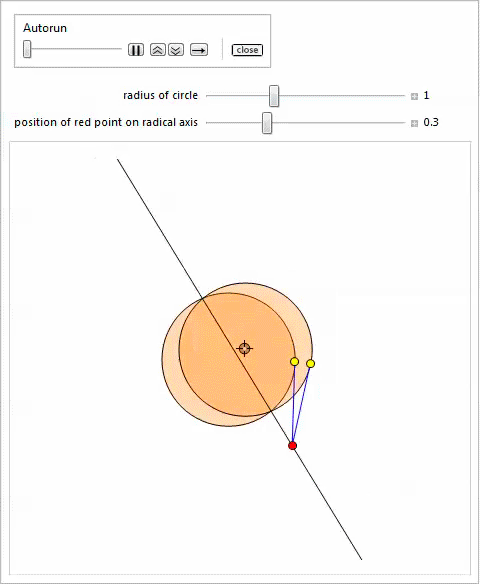
以下のManipulateのデモでは、2つの円を示しています。 1つは固定されており、他の円のサイズと中心は、ロケーターを移動し、スライダーの位置を変更することで変更できます。 別のスライダーを使用して、ラジカル軸上の赤い点の位置を変更して、定理4を説明できます。

二次元と三次元のアルベロスの交差点

このデモは、2つの一般化を示しています。





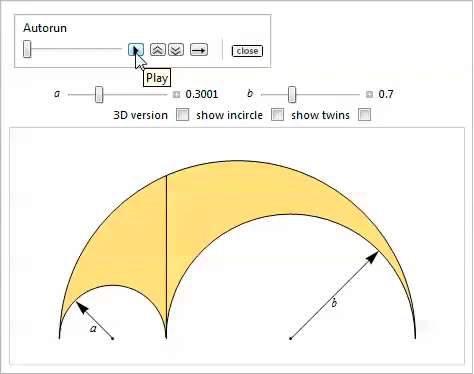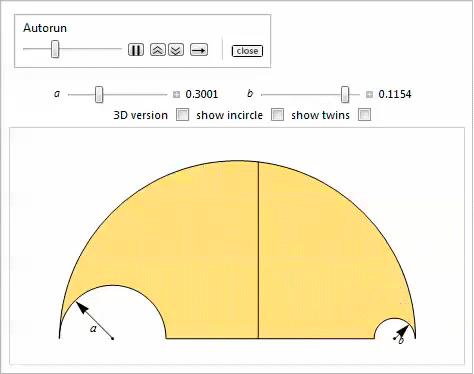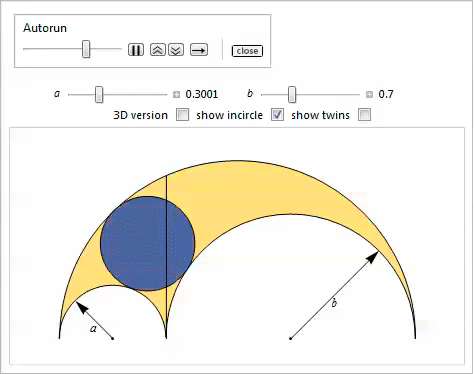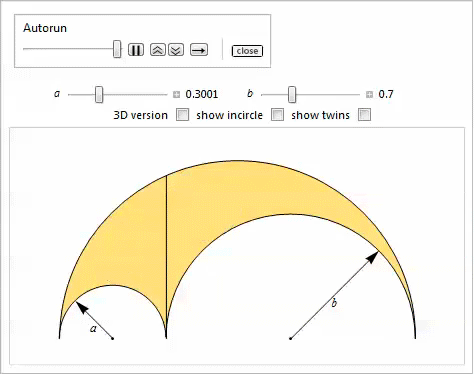物件28
内接円は、外側および上部のアーチのラジカル軸に接触し、一般化されたアルベロスの各アークは同じ半径を持っています。

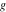
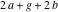
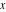
させる -ベース間のギャップの長さ（つまり、上部アークの直径は ）としましょう -ラジカル軸と軸の交点の横座標 、開始点がアルベロスの極左点にあると仮定します[10]。

定理5
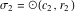
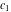
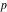
円が そして 交差しない場合、それらのラジカル軸はセグメントと交差します その時点で そのように 。

この定理を使用して、値を計算します 。





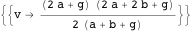
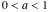
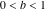
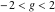
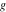
一般化を失うことなく、我々はそれを仮定することができます 、 、そして （ 負の値を取る場合があります）。 内接円を次のように呼び出します そして 。 これらのパラメータの値は、次のように取得されます。





次に、少なくともいくつかの中心を無視することができますが、半径はいずれの場合も同じになります。

言葉のない証明

実際、ここにはアルベロスの3つのプロパティがあります。 どのプロパティが関係しているかを推測できるかどうか、コントロールを試してみましょう[24,25]。

最初の操作では、サイドアーチを移動できます。





2番目の操作では、サイドアーチのタッチポイントを中心に線を回転できます。





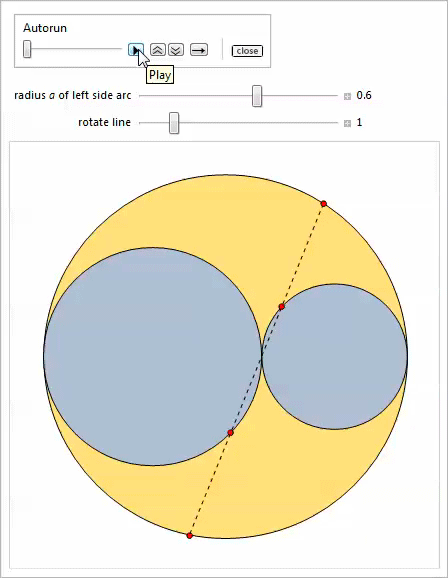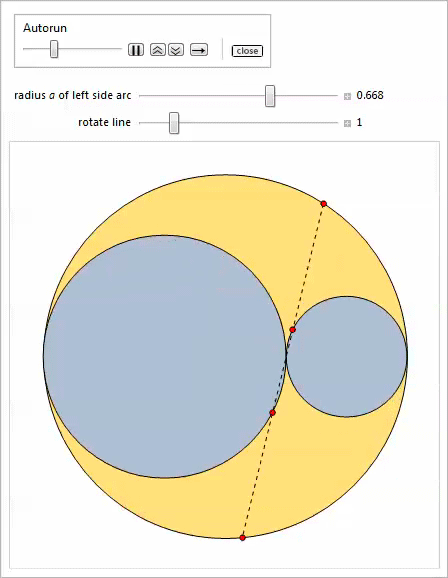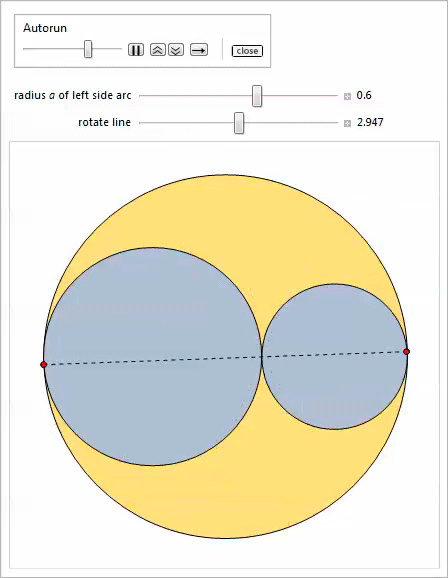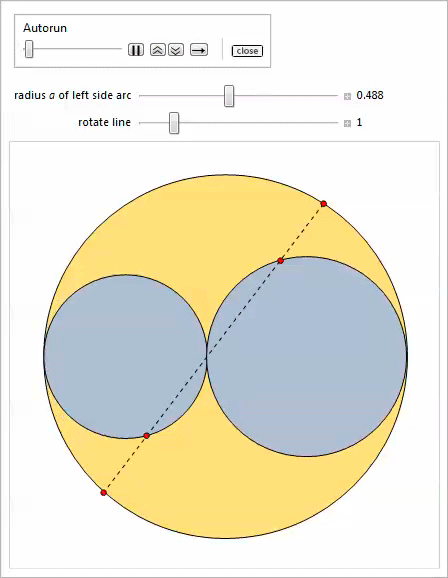
最後に、3番目のManipulateは、双子の無限のファミリーを特徴としています。

参照資料

[1] F.ヴァンラモーエン。 「アルキメデスのサークルのオンラインカタログ」（2014年1月22日） home.planet.nl/~lamoen/wiskunde/arbelos/Catalogue.htm

[2] S.ガルシア・ディートヘルム。 Wolframデモンストレーションプロジェクト— Wolfram Webリソースの「平面応力回転」。 demos.wolfram.com/PlanarStressRotation 。

[3] CW Dodge、T。Schoch、PY Woo、およびP. Yiu、「それらのユビキタスアルキメデスの円」、 Mathematica l Magazine、 72 （3）、1999ページ。 202-213。 www.jstor.org/stable/2690883

[4] HP Boas、「Reflection on the Arbelos」、 American Mathematical Monthly 、 113 （3）、2006ページ。 236-249。

[5] HDDörrie、 初等数学の100の大きな問題：その歴史と解決策 （D. Antin、trans。）、ニューヨーク：Dover Publications、1965。

[6] J.Rangel-Mondragón。 Wolframデモンストレーションプロジェクト— Wolfram Webリソースの「再帰演習II：パラドックス」。 demos.wolfram.com/RecursiveExercisesIIAParadox 。

[7] RB Nelsen、「言葉のない証明：アルベロスの領域」、 Mathematics Magazine 、 75 （2）、2002 p。 144。

[8] A.ガダラ。 Wolfram Demonstrations Project — A Wolfram Web Resourceの「Area of​​ the Arbelos」。 demos.wolfram.com/AreaOfTheArbelos 。

[9] J.Rangel-Mondragón、「計算上の非ユークリッド幾何学で選択されたテーマ。 パート1.逆幾何学の基本的な特性」、 The Mathematica Journal 、2013年。 www.mathematica-journal.com/2013/07/selected-themes-in-computational-non-euclidean-geometry-part-1

[10] D. Pedoe、 Geometry：A Comprehensive Course 、ニューヨーク：Dover、1970。

[11] M.シュライバー。 Wolfram Demonstrations Project — A Wolfram Web Resourceの「Orthogonal Circle Inversion」。 demos.wolfram.com/OrthogonalCircleInversion 。

[12] MGウェルチ、「アルベロス」、修士論文、1949年カンザス大学数学部

[13] L.バンクオフ、「The Marvelous Arbelos」 、数学の軽い側面 （RK GuyとRE Woodrow編）、ワシントンDC：アメリカ数学協会、1994年。

[14] GLアレクサンダーソン、「レオンバンクオフとの会話」、 The College Mathematics Journal 、 23 （2）、1992ページ。 98-117。

[15] S.カバイ。 Wolfram Demonstrations Project — A Wolfram Web Resourceの「Tangent Circle and Arbelos」。 demos.wolfram.com/TangentCircleAndArbelos

[16] G.マルコフスキーとC.ウルフラム。 Wolframデモンストレーションプロジェクト— A Wolfram Webリソースの「フクロウの目の定理」。 demos.wolfram.com/TheoremOfTheOwlsEyes 。

[17] PY Woo、「Arbelosの内接円の単純な構成」、 Forum Geometricorum 、1、2001ページ。 133-136。 forumgeom.fau.edu/FG2001volume1/FG200119.pdf

[18] B.アルパート。 Wolframデモンストレーションプロジェクト— A Wolfram Webリソースの「アルキメデスの双子の円」 demos.wolfram.com/ArchimedesTwinCirclesInAnArbelos 。

[19] J.Rangel-Mondragón。 Wolfram Demonstrations Project — A Wolfram Web Resourceの「Twins of Arbelos and Circles of a Triangle」 demos.wolfram.com/TwinsOfArbelosAndCirclesOfATriangle 。

[20] H.奥村、「歪んだアルベロスの双子円の詳細」、 フォーラム幾何学 、11、2011、pp。 139-144。 forumgeom.fau.edu/FG2011volume11/FG201114.pdf

[21] EWヴァイスシュタイン。 Wolfram MathWorldからの「ポイントライン距離— 2次元」— Wolfram Webリソース。 mathworld.wolfram.com/Point-LineDistance2-Dimensional.html

[22] L.バンクオフ、「アルキメデスの双子の円は本当に双子ですか？」、 Mathematics Magazine 、 47 （4）、1974 pp。 214-218。

[23] F. Power、「アルベロスのアルキメデスの輪」、 フォーラムGeometricorum 、5、2005、pp。 133-134。 forumgeom.fau.edu/FG2005volume5/FG200517.pdf

[24] AV Akopyan、 図の幾何学 、CreateSpace Independent Publishing Platform、2011。

[25]奥村H.および渡辺M.、「アルキメデスの円の無限集合の特性」、 フォーラム幾何学 、7、2007、pp。 121-123。 forumgeom.fau.edu/FG2007volume7/FG200716.pdf