Habrの最初の記事を書くというアイデアは、サーバーシステムを作成するための「石の収集」プロセスで生まれました。その主なタスクは次のとおりです。
- いくつかの典型的な連続的な「重い」計算のためにユーザーからアプリケーションを受け取ります。
- 計算の実装。
- 残りの計算時間に関する情報の発行(要求に応じて);
- 完了時に計算結果が発行されます。

研究の多くの状況を明確にする必要があります。
- 逐次計算とは、複数のプロセッサコア(非並列化可能プロセス)によって実行される計算を意味します。 システムを作成するこの段階では、計算自体を並列化するタスクには価値がありません。 将来、「シーケンシャル」という単語は省略されます。
- 計算は典型的です、すなわち 同じアルゴリズムが計算に使用されます。特定のコンピューティングシステムの実行時間は、実際の値ではなく、主にソースデータの次元(次元は数値Nで示されます)に依存します。
- 計算は主に「重い」と想定されており、完了するにはかなりの時間(数秒から数時間、場合によってはそれ以上)が必要です。
- 計算の適用の強度の変化の性質と、次元Nの対応する値が想定されます。
計算時間を予測しようとする著者の最初の試みは精度が低かった。 「目による」アルゴリズムでは、平均偏差を最小化するために、Nに対する時間の依存性がべき乗係数を使用して選択されました。 このようなテスト計算の結果、あまり快適な結果は得られませんでした。
| N | リアルタイム(秒) | 推定時間(秒) |
| 417 | 9.60 | 5.04±0.96 |
| 689 | 26,20 | 18.33±3.50 |
| 1165 | 78.40 | 70.56±13.48 |
| 2049 | 264.60 | 300.34±57.40 |
| 3001 | 654.20 | 799.24±152.74 |
| 3341 | 875.80 | 1,052.50±201.13 |
| 4769 | 2323.60 | 2 621.69±501.01 |
| 5449 | 3424.10 | 3 690.10±705.18 |
| 6129 | 4811.80 | 4 988.97±953.40 |
よくあることですが、これを助けるために、古典が登場しました。 長い間忘れられていた「補間」、「外挿」という言葉を思い出し、選択された方向の正しさを疑ってインターネットで検索が開始されました。 多くの投稿、記事、その他のリソースが再読されました。 主な結論は次のとおりです。1つの変数の未知の関数の値を予測する問題を解決するために、チェビシェフまたはラグランジュ多項式が最もよく使用されます。 既存の「引数値」のセットに信頼がなく、逆の場合はラグランジュ多項式が適している場合、チェビシェフ多項式を使用するのが理にかなっていることがわかりました(原則として、MNCもそれらを置き換えることができます)。 2番目は必要なものに見えました。 実際、特定のシステムで計算アルゴリズムをテストするための「理想的な」条件を作成し(100%の負荷でカーネルを割り当て)、ラグランジュ多項式を構築するのに十分な統計を収集してみませんか?
一方、ラグランジュ多項式を構築するためにすでに実装されているアルゴリズムは、たとえば
ここにあります 。 タスクに適応したアルゴリズムは、増加する統計セットに外挿すると同様の(モジュロ偏差)結果を示し始めました(N = 1165の予測では、N = 417およびN = 689でリアルタイムが使用され、N = 2049での予測ではN = 417、N = 689およびN = 1165など):
| N | リアルタイム(秒) | 推定時間(秒) |
| 417 | 9.60 | - |
| 689 | 26,20 | - |
| 1165 | 78.40 | 55.25 |
| 2049 | 264.60 | 253.51 |
| 3001 | 654.20 | 617.72 |
| 3341 | 875.80 | 863.74 |
| 4769 | 2323.60 | 2899.77 |
| 5449 | 3424.10 | 2700.96 |
| 6129 | 4811.80 | 5862.79 |
ラグランジュ多項式で補間すると、N = 2049から結果が印象的でした(1つの測定がサンプルから順次除外され、除外された測定の引数に従って計算が行われました)。
| N | リアルタイム(秒) | 推定時間(秒) |
| 417 | 9.60 | - |
| 689 | 26.20 | 2,58 |
| 1165 | 78.40 | 98.35 |
| 2049 | 264.60 | 245.74 |
| 3001 | 654.20 | 664.15 |
| 3341 | 875.80 | 862.91 |
| 4769 | 2323.60 | 2,407.75 |
| 5449 | 3424.10 | 3251,71 |
| 6129 | 4811.80 | - |
実際、N = 689およびN = 1165の場合、予測値の実際の値からの偏差はそれぞれ約
90%および25%でしたが、これは許容できませんが、N = 2049以降では、偏差は
1.5-7%以内に維持され
ました良い結果として扱います。
多項式: F(x)= -5.35771746746065e-22 * x ^ 7 + 1.23182612519573e-17 * x ^ 6-1.14069960055193e-13 * x ^ 5 + 5.44407657742344e-10 * x ^ 4-1.39944148088413e-6 * x ^ 3 + 0.00196094886960409 * x ^ 2-1.22001773413031 * x + 263.749105425487
必要に応じて、アルゴリズムの次数をわずかに変更することにより、多項式の次数を必要なものに減らすことができます(原則として、著者のタスクのために3次は不要です)
この多項式のグラフ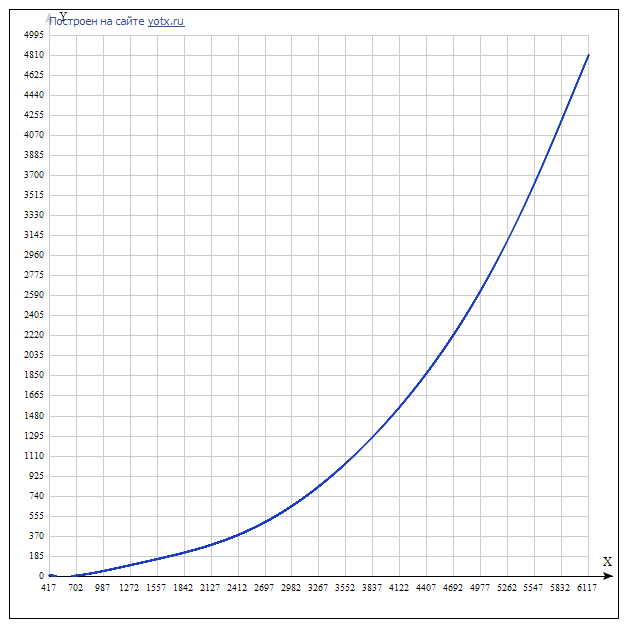
多項式は補間であることに注意することが重要です。つまり、範囲[N
min ; N
max ]の範囲外の値に対しては、予測の質には多くのことが望まれます。
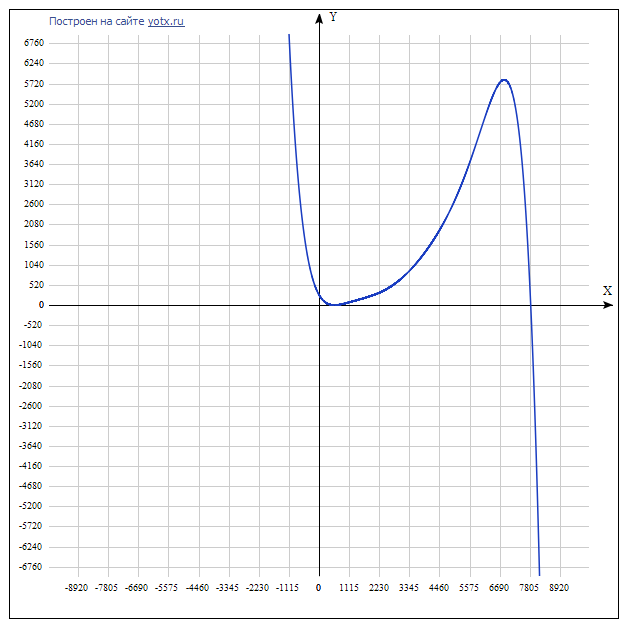
結論: 「理想的な」条件下(特にNの値が大きい場合)で事前に十分な統計を収集し、ラグランジュ多項式を構築し、アプリケーションの受信時に、完成した多項式にN iを代入して計算時間の予測を受け取ることは理にかなっています。このアプローチは非常に明確ですが、プロプロセッサ(マルチコア)システムについて話すとき、状況はより複雑になります。
- まず、上記のアプローチは、アプリケーション(実行されるタスク)の数がX <= Y(Yはコアの数)の場合に適しています。 つまり、システムは計算のみを行い、各タスクには対応するコアの100%リソースが提供されます。
- 次に、X> Yの場合、OSはタスク間でコンピューティングリソースを共有する必要があります(たとえば、Ubuntuサーバー14.04で画面からタスクを手動で開始する場合、コンピューティングリソースはX / Y * 100%の式に従ってタスク間で均等に分割されました)。
- 第三に、アプリケーションの受信と対応するNの値の性質は事前にわからないため、コンピューティングリソースの分布式(たとえば、同じX / Y * 100%)を使用して時間を予測することはできません。
これらの側面の分析により、リードタイムを事前に予測することは不可能であることが示されましたが、この値は、計算に割り当てられた現在のコンピューティングリソースに影響するイベントが発生したときに調整し、ユーザーに発行できます。 そのようなイベントは次のとおりです。
新しいタスクの到着とタスクの
完了 。 これらのイベントが発生すると、予測の修正が提案されます。
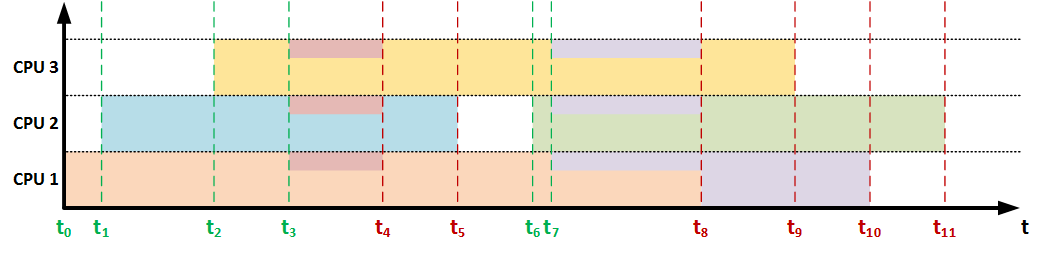
これらのイベントのいずれかが発生すると、各タスクに割り当てられたリソースを再計算する必要があることが明らかになります(タスク間のリソースの既知の分布の場合)、または組み込み(言語または操作)手段を使用して何らかの方法でこの値を取得し、残りの時間を再計算する必要があります割り当てられたリソースを考慮に入れます。 ただし、このためには、プロセスによってすでに完了している作業の量を知る必要があります。 そのため、必要な情報を含むストレージ(DBMSのテーブルなど)を整理することをお勧めします。たとえば、次のとおりです。
| タスクID | 開始する | 終わり | ラグランジュ(N) | 完了 | 最後のリクエスト | 最終修正 | 現在のCPU |
| 2457 | 12:46:11 | ... | ラグランジュ(N) | 0.45324 | ... | 12:46:45 | 1.00 |
| 6574 | 12:46:40 | ... | ラグランジュ(N) | 0,08399 | ... | 12:46:45 | 1.00 |
| 2623 | 12:44:23 | 12:46:45 | ラグランジュ(N) | 1.00 | ... | 12:46:45 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... |
次のアルゴリズム(メタコード)を実装することになっています。
- ユーザーがタスクステータスを要求する場合:
- <Done> + =(<Request Moment>-MAX(<Last Request>、<Last Correction>))* <現在のCPU> / <Lagrange(N)>;
- <最後のリクエスト> = <リクエスト時間>;
- ユーザー<Done>および<Current CPU>に戻ります。
- 新しいタスクが到着すると:
- 新しい<タスクID>を作成します。
- <Start>に実行の開始時間を記録します。
- <Lagrange(N)>の「理想的な」条件下で実行時予測を計算して記録します。
- <完了> = 0;
- <最後のリクエスト> = 00:00:00;
- 修正手順を呼び出します。
- タスクの最後に、レコードを完全に削除できますが、いずれにしても、修正手順を呼び出します。
- 修正手順:
- すべてのエントリの場合:<最終修正> = <現在時刻>(この値を別の場所に保存することは理にかなっています);
- 各タスクの対応する<Current CPU>を取得して記録します。
結論: 「理想的な」条件の事前予測を行うことで、システムの負荷が変化したときに「重い」逐次計算の予測割合を実際に「オンザフライ」で調整し、要求に応じてこれらの値をユーザーに提供できます。特定の実装には、人生を複雑化または単純化する独自の特性がある場合がありますが、この記事の目的は、デリケートなケースを分析することではなく、読者の公正な裁判に対する上記のアプローチを提供することです(主に実行可能性に関して)。