気象効果の実現。 降水量

天気の影響を正しくシミュレートするタスクは、ゲーム業界のまさに設立からほぼ伸びています。 天気は私たちの生活の不可欠な部分です。つまり、天気の影響のないゲームは完全ではありません。 これが、珍しいゲームが少なくとも非常に原始的な天気シミュレーションなしで行う理由です。 タスクは非常に古いため、明らかに効率が低いにもかかわらず、現在も使用され続けている多くの古いソリューションがあります。 そして、通常の霧ですべてが単純な場合、降水量の実装は特定の困難を引き起こします。

では、現実の世界で雨や雪とは何ですか？

これらは、地球自体から雲までの空間をほぼ均等に埋める数十億個の小さな粒子です。 無制限のコンピューティングリソースがある場合-降水量をシミュレートするために行う必要があるのは、場所に均等に分散されたこの10億個の粒子を処理することだけです。 しかし、私たちの計算能力は非常に限られており、地形、物体、その他すべてを含まない場所が降水のみで構成される場合に限り、リアルタイムで100万個の粒子でさえ計算できます。 十億について何と言えますか。

この点で、降水量を実装するプロセスでは、3つの個別のタスクに直面します。

• パーティクルの数を10億から許容可能な20〜5万に減らします。
• 各パーティクルの計算量を最小限に減らします。
• すべてのコンピューティングをGPUに転送します。

まず、これをどのように達成するかを検討してください。
単純な結論に基づいて、パーティクルの数を減らします。オブザーバーは10億個のパーティクル全体を見ることはありません。 彼は彼の後ろに、あまりにもはるかに上下に粒子を見ません。 これにより、すでにパーティクルの数が3〜4回削減されます。 しかし、2億は多すぎます。 ここで私たちの助けに少しのトリックが来ます。 実際には、粒子は非常に小さく、実際にはすでに数メートルの距離で均一なベールに変わります。 したがって、「正直に」、約10メートルの距離で観測者の前にパーティクルのみを描画する必要があります。 これらの条件下での50,000個の粒子は、非常に密な降雪の外観を作成するのに十分です。 現実の世界では、粒子サイズはミリメートル単位で測定されることを理解することも重要です。 コンピュータシミュレーションの場合、粒子サイズを数センチメートルまで簡単に増やすことができます。 オブザーバーには、粒子を調べ、そのサイズを周囲のオブジェクトと比較する機会がありません。

以下は、次の設定の降雪のある場所です。15メートル以内の粒子数25,000、粒子サイズ-10センチメートル、20〜100メートルの距離で密度80％の白い霧。



降水が無効になっている同じ場所を次に示します。



粒子サイズが不自然に大きいという事実にもかかわらず、これは観察者によって絶対に正常であると認識されます-結局のところ、彼は粒子までの距離を推定することができず、大きな粒子は非常に近いため大きいと思われます。 現実にはそうではありませんが。

2番目の重要なタスクは、各パーティクルの計算を最小限に抑えることです。 各フレーム内の25,000個のパーティクルでさえ、目に見える負荷です。 したがって、少しでも最適化が重要です。 それで、思い出してみましょう：私たちが素直にそれをとるならば、私たちは粒子に対してどんな計算をする必要があるのか​​：

• XYボリュームのランダム座標での発生
• 重力加速
• Z空気抵抗
• X、Y空気抵抗（風）
• ジオメトリとの交差（粒子が、観察者がいる家の屋根などの障害物を通過しないようにするため）。

これらのパラメータは、正確なシミュレーションに取り組んでいる場合に非常に重要です。 ただし、ゲームでは、視覚的コンポーネントが重要であり、物理シミュレーションの精度ではありません。 オブザーバーには特定の粒子の挙動を追跡する機会がないため、ランダム性と正直な計算を安全に取り除くことができます。 粒子が変更せずにサイクルからサイクルへ同じパスを通過しても、オブザーバーはこれに気付かないでしょう。 別の24,999個のパーティクルがパスに沿って近くに移動します（ループしている場合でも）。
したがって：

• 粒子は常にブロックに対して同じ座標に表示されます。 これらの座標は、頂点バッファーを介して送信される座標です。
• Zの加速と抵抗は無視し、互いに重なると考えます。 つまり、パーティクルは一定の速度で移動します。
• 正直な計算を無視し、粒子の初期XY座標に風速*時間を追加します。
• すべての静的ジオメトリを高さマップにベイク処理し、粒子のZ位置と粒子の高さをXY座標で単純にチェックします。 この時点で粒子が高度を下回った場合-描画しません。

ジオメトリとの単純化された交差が常に機能するとは限らず、場合によってはアーティファクトが作成されることもあります。 視覚的には、ボイドからの粒子の外観のように見えます。



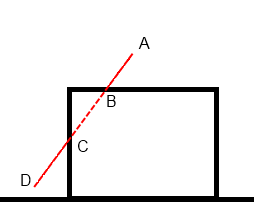
パーティクルは、家の上にあるポイント「A」でパスを開始し、ポイント「B」まで下降する限り、すべて正常です。 彼女は幾何学の上にいます。 彼女が高さ「B」を越えるとすぐに、彼女は見えなくなりました。 屋根の下にあります。 これは、ポイント「C」を通過するまで続きます。 風の影響により、粒子は家の外に移動し、ジオメトリよりも高いことが判明しました。その結果、粒子は再び見えるようになりました。 視覚的には、家の壁から粒子が「見える」ように見えます。 これはかなり不快なアーティファクトであり、存在することを念頭に置く必要があります。 粒子ベクトルとジオメトリの交差を「正直に」計算しようとすると、降水システムの動作が非常に遅くなる危険があります。 しかし、かなり単純なヒントがあります。風による粒子の偏差に従って高さマップを変更します。

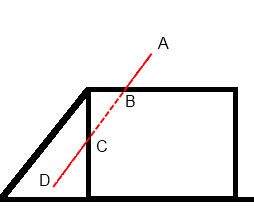
このソリューションの唯一の欠点は、風が変わったときに標高マップを再構築する必要があることです。

Igrostroyは常にアーティファクトと速度の妥協点であり、このケースはそのような妥協案の一例にすぎません。 アーティファクトは、風速が高いほど顕著になります。

最適化の最後の段階は、コンピューティングのGPUへの移行です。 実際、前のステップの後に特別な計算はありませんでした。

XY座標は、原点と風によって追加されたオフセットから計算されます。
XY = Start.xy +風*時間;
Z座標は、落下速度の初期座標から時間を引いて計算されます。
Z = Start.z-速度*時間
さて、最後に-粒子の可視性は、この点で得られたZ座標とジオメトリの高さを比較することで決定されます。
IsVisible = MapHeight（XY）<Z

これら3つの操作はすべて、GPUに簡単に転送できます。 観察者からの距離、照明の使用、その他のささいなことを考慮して、透明度の計算もあります。 しかし、それらはすでにGPUに適用されており、明らかに、転送中に問題になることはありません。

上記のすべての特定の実装の説明に進む前に、実装の別の重要な側面について詳しく説明する価値があります。 つまり、作成したパーティクルのブロックを世界のどこに描画するか、およびどのような形状にするかを決定する際に。

実装時に最初に頭に浮かぶのは、円柱の一部であり、観察者の座標と錐台の面に沿ったセクションを中心としています。



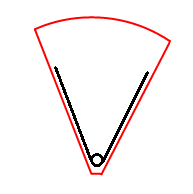
これは非常に魅力的なオプションです。 結果として生じる円柱の一部内でのみ粒子を生成するため、観察者が見るゾーンでのみ作業することができます。 つまり、生成された50,000個のパーティクルのほぼすべてが画面に表示されます！ とても経済的です！ しかし、観察者にカメラを動かしたり回転させたりする能力を与えると、すべてが壊れます。 粒子が錐台の内部に残るためには、観測者とともに円柱を移動する必要があります。 つまり、観察者がどのように移動して回転するかに関係なく、彼は常に同じ粒子を見ます！ これはダメです。 したがって、別のオプションに焦点を当てます。退化した粒子がたくさんありますが、カメラの回転と移動は粒子システムの仕事を壊しません。カメラを移動して回転させると、実際には同じ粒子ですが、新しい粒子を見ているように感じます粒子。

アイデアは、キューブの形のゾーンで作業しているということです。 初期初期化中に、粒子は立方体の寸法に従ってXoY平面にランダムに配置されます。

粒子座標は、ブロックのサイズで世界の原点にある正方形のピースを塗りつぶします。



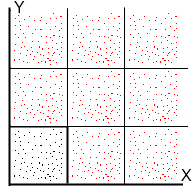
黒い点は、そのまま粒子の座標を示します。 赤は同じ粒子で、ブロックのサイズによってのみ相殺されます。 仕組み：観測者の錐台があります。 キューブを取り、錐台に入れます。 刻印の主な条件は3つです。

1）ユニットは回転しません。 碑文は移動することによってのみ実行されます。
2）オブザーバーの座標はブロックに含まれている必要があります。
3）観察者から錐台の両面とブロックの側面の交点までの距離は、できるだけ等しくする必要があります。

錐台にブロックを刻んだ後、次のような結果が得られます。



錐台は私たちのブロックよりもはるかに大きいですが、問題ではありません。 粒子は、観測者からわずか数メートル離れている必要があります。

内接ブロックの座標を取得したら、風の適用を考慮して、各粒子のXY座標を計算します。 簡単にするために、この例では、風がないため、粒子の座標はXY座標を変更していないと仮定します。



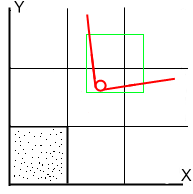
内接ブロックに入るように、各パーティクルを移動します。 これを行うには、XとYのパーティクルを移動しますが、スムーズではなく、ブロックのサイズに等しいステップで移動します。



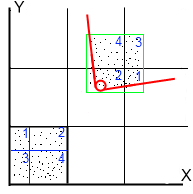
粒子はそれぞれ単独ではなく、ブロック単位で移動することがわかります。 たとえば、ブロック「1」に入る粒子は、Xに沿って2サイズ、Yに沿って1サイズ移動します。

したがって、すべての粒子は、グリッド上の変位に応じて、投影上のゾーン内にあります。
移動すると、オブザーバーはゾーンを移動し、パーティクルはそれぞれ新しい投影に移動します。
たとえば、オブザーバーが現在の位置からXから右に移動すると、ブロック「4」と「2」が減少し、逆にブロック「3」と「1」が増加します。 左側のゾーンから落下する粒子は、右側にジャンプします。 その結果、移動すると、観測者はますます多くの新しい粒子を見ますが、実際にはこれらはゾーンから落ちた古い粒子です。 回転の場合と同じ状況で、観察者の位置が変わってもゾーンだけは変わりませんが、錐台の境界が変わるためです。

実用的な実装

すべての堆積物粒子は1つのDIPで描画されます。 頂点バッファーは静的に一度初期化され、変更されません。 各パーティクルは1つの頂点で表され、ブロック内にランダムなXYがあります。 ジオメトリシェーダーは、上からパーティクルを作成します。 雪の例で作られました。 雨の場合は、球形の看板ではなく、円筒形のものを使用する必要があります。 そして、それに応じて、粒子は正方形ではなく、長方形です。

すべての粒子に対してグローバルに次のデータが必要です。
mat4 ModelViewProjectionMatrix; -座標をモデル空間からカメラ空間に変換し、スクリーン平面に投影するための投影モデルビューマトリックス。
フロート時間; -秒単位のグローバル時間。
フロート速度; -粒子落下率;
フロートトップ; -粒子が落下し始める高さ;
フロート底; -粒子の落下が止まる高さ。
float CircleTime; -粒子が最高点から最低点に移動する時間。
vec2風; -風速;
float TileSize; -ブロックサイズ。
vec2 Border; -ブロック座標。 ブロックの左上隅。 右下はBorder + vec2（TileSize、TileSize）です。
float ParticleSize; -粒子サイズ;
sampler2Dテクスチャ。 -粒子のテクスチャ。

各パーティクルの属性：
vec2位置; -位置。 この値はブロック内でランダムに設定されます。 Z座標が設定されていないのは、 シェーダー内で計算されます。
float TimeShift; -0を基準とした時間のパーティクル変位。値はCircleTime内でランダムに設定されます。

この値をTimeに追加すると、パーティクルのランダムな開始位置が取得されます。
float SpeedScale; -0.9-1.1の範囲のランダムな値。 このSpeedの値を乗算すると、パーティクルごとにわずかに異なる速度が得られます。
頂点シェーダー：

uniform mat4 ModelViewProjectionMatrix; uniform float Time; uniform float Speed; uniform float Top; uniform float Bottom; uniform float CircleTime; // (Top-Bottom)/Speed uniform vec2 Wind; uniform float TileSize; uniform vec2 Border; in vec2 Position; in float TimeShift; in float SpeedScale; out vec4 Position3D; void main(void) { float ParticleCircleTime = CircleTime / SpeedScale; float CurrentProgress = mod(Time + TimeShift, ParticleCircleTime); vec3 Pos = vec3(Position.xy + Wind*CurrentProgress , Top - Speed*SpeedScale*CurrentProgress); Pos.x = mod(Pos.x, TileSize); Pos.y = mod(Pos.y, TileSize); float c; c = floor(Border.x/TileSize); if (c*TileSize+Pos.x < Border.x) Pos.x = Pos.x + (c+1)*TileSize; else Pos.x = Pos.x + c*TileSize; c = floor(Border.y/TileSize); if (c*TileSize+Pos.y < Border.y) Pos.y = Pos.y + (c+1)*TileSize; else Pos.y = Pos.y + c*TileSize; Position3D = ModelViewProjectionMatrix * vec4(Pos,1.0); } 

幾何学的なシェーダー：

 layout(points) in; layout(triangle_strip, max_vertices=12) out; const vec3 up = vec3(0.0,1.0,0.0); const vec3 right = vec3(1.0,0.0,0.0); uniform vec2 ParticleSize; in vec4 Position3D []; out float TexCoordX; out float TexCoordY; void main(void) { vec3 u = up * vec3(ParticleSize.y); vec3 r = right * vec3(ParticleSize.x); vec3 p = Position3D[0].xyz; float w = Position3D[0].w; gl_Position = vec4 ( p - u - r, w ); TexCoordX = 0.0; TexCoordY = 1.0; EmitVertex (); gl_Position = vec4 ( p - u + r, w ); TexCoordX = 1.0; TexCoordY = 1.0; EmitVertex (); gl_Position = vec4 ( p + u + r, w ); TexCoordX = 1.0; TexCoordY = 0.0; EmitVertex (); EndPrimitive (); // 1st triangle gl_Position = vec4 ( p + u + r, w ); TexCoordX = 1.0; TexCoordY = 0.0; EmitVertex (); gl_Position = vec4 ( p + u - r, w ); TexCoordX = 0.0; TexCoordY = 0.0; EmitVertex (); gl_Position = vec4 ( p - u - r, w ); TexCoordX = 0.0; TexCoordY = 1.0; EmitVertex (); EndPrimitive (); // 2nd triangle } 

フラグメントシェーダー：

 uniform sampler2D Texture; in float TexCoordX; in float TexCoordY; out vec4 color; void main(void) { color = texture(Texture, vec2(TexCoordX, TexCoordY)); } 

与えられたシェーダーが何をするかを詳しく見てみましょう。
すべての基本的な操作は、頂点シェーダーで実行されます。 ジオメトリシェーダーはポイントをボリュームパーティクルにアンパックしますが、フラグメントシェーダーは単にテクスチャを適用します。 コードが単純であるため、ジオメトリシェーダーとフラグメントシェーダーは考慮されません。

頂点シェーダーを考えてみましょう：
最初に行う必要があるのは、パーティクルが現在どの位置にあるかを調べることです。 私たちの位置は時間に結びついているため、時間を計算する必要があります。 これは、2つの操作で行われます。

float ParticleCircleTime = CircleTime / SpeedScale;
float CurrentProgress = mod（Time + TimeShift、ParticleCircleTime）;
最初の行は、特定の粒子のサイクルに合計サイクル時間を与えます。 なぜなら サイクルは速度に依存し、SpeedScaleでは速度が異なるため、必要なことは、合計サイクル時間を速度係数で除算することだけです。

2行目では、現在のグローバルパーティクル時間を取得し、1サイクルの時間で除算し、CurrentProgressの除算の残りを取得します。 これは、特定のパーティクルの現在のサイクルの開始から経過した時間です。

次のステップは、経過時間に従って位置を計算することです。 XYを計算するには、風から受け取ったオフセットを開始位置に追加する必要があります（Zの場合）-落下速度に時間を掛けます。
vec3 Pos = vec3（Position.xy + Wind * CurrentProgress、Top-Speed * SpeedScale * CurrentProgress）;
粒子は風によりブロックの外を飛ぶ可能性があるため、粒子をブロックに戻す必要があります。
Pos.x = mod（Pos.x、TileSize）;
Pos.y = mod（Pos.y、TileSize）;
その結果、ブロック内の粒子の座標を取得します。



ただし、原点ではなく、観測者の周囲にパーティクルが必要です！ この点に関して、粒子を錐台の周りで説明したゾーンに移動します。

c = floor（Border.x / TileSize）;
if（c * TileSize + Pos.x <Border.x）
Pos.x = Pos.x +（c + 1）* TileSize;
他に
Pos.x = Pos.x + c * TileSize;

c = floor（Border.y / TileSize）;
if（c * TileSize + Pos.y <Border.y）
Pos.y = Pos.y +（c + 1）* TileSize;
他に
Pos.y = Pos.y + c * TileSize;


投影された座標はスクリーンに投影されます：Position3D = ModelViewProjectionMatrix * vec4（Pos、1.0）;

次に、ジオメトリシェーダーが頂点をパーティクルにアンパックします。

上記のコードは、snowの最も単純な実装です。 グローバルライティング、点光源、ジオメトリとの交差点の追加-タスクは非常に簡単で、自分で処理できると思います。 また、粒子だけではシャワーや降雪を作り出すのに十分ではないことを忘れないでください。 粒子はあまり多くありません。 この状況では、霧が助けになり、その助けを借りて雪や雨の覆いが作られます。

注：
この記事は数年前に未出版の本の一部として書かれました。
かなり大規模なプロジェクトで作業を完了した後、振り返ってみると、長年の開発の間に、興味深い話題になる可能性のあるタスクがあることがわかりました。 その結果、本が登場しました。 この本は2012年に執筆および編集されましたが、どこにも出版されていません。 対象読者は明確ではありませんでした。

今日、私はこの本のテキストに出会い、おそらくそれからいくつかの章がHabrコミュニティにとって興味があると思いました。

テストとして、天気効果の実装に関する章を公開します。 コミュニティがこの記事を歓迎している場合は、あと数章を公開します。