内容

1. テンソルとは何ですか、なぜ必要ですか？
2. ベクトル演算とテンソル演算。 テンソルランク
3. 曲線座標
4. テンソル博覧会のポイントのダイナミクス
5. テンソルのアクションとその他の理論的な質問
6. 自由固体の運動学。 角速度の性質
7. ソリッドの最終回転。 回転テンソルのプロパティとその計算方法
8. Levi-Civitaテンソルの畳み込みについて
9. 最終回転のパラメーターによる角速度テンソルの導出。 頭とマキシマを適用
10. 角速度ベクトルを取得します。 欠点に取り組む
11. 自由な動きでの体のポイントの加速。 ソリッドの角加速度
12. 固体運動学におけるロドリゲハミルトンパラメーター
13. テンソル式の変換の問題におけるSKA Maxima。 ロドリゲ・ハミルトンのパラメーターにおける角速度と加速度
14. 剛体のダイナミクスの非標準的な紹介
15. 非自由な固体運動
16. 固体の慣性テンソルの特性
17. ナットジャニベコバのスケッチ
18. ヤニベコフ効果の数学的モデリング

はじめに

不可解なほど嬉しい読者は、 前の記事が好きでした。 私はすぐに予約をします-テンソルがうまくいかないような大容量の概念について話すために-多くの情報があります。 サイクルの終わりまでにモザイクが発達すると約束できます。

そして最後に、斜めベースでベクトルの表現を調べ、それが2つの異なる（共変および反変）座標セットによって表されることを決定したという事実に落ち着き、空間メトリックの変化を考慮したスカラー積の一般式を得ました。 したがって、我々は非常に慎重にテンソルの概念にアプローチしました

テンソルは、座標系が変化しても変化しない数学的なオブジェクトであり、そのコンポーネントのセットと基底を変更するときのコンポーネント変換ルールによって表されます。

スカラー作業は良好です。 しかし、残りの操作はどうでしょうか？ それらは空間の幾何学とどのように関係し、テンソル形式で表現可能ですか？ もちろん、ベクトルは...テンソルなので、想像できます！ また、スカラーもテンソルです。 おなじみの数学的オブジェクトは、より一般的な概念、つまりテンソルの特定の例にすぎません。

それは私たちがカットの下で話をするものです。

1.計量テンソルの幾何学的意味

推論の一般性にあまり影響を与えない明確にするために、3次元空間に制限します。 次のステートメントを証明しましょう-計量テンソルの行列式は、基底ベクトルにまたがる平行六面体の体積の二乗に等しいです。




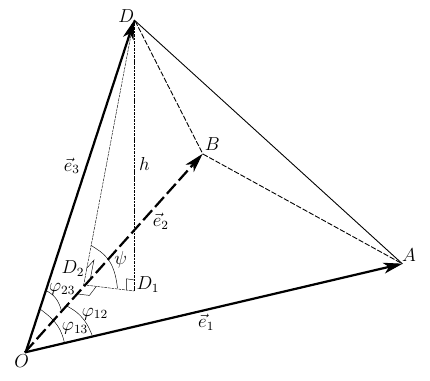
図 1.基底によって形成される三面角の関係

任意の基礎を考える


ステレオメトリーで一般的なように、基底まで引き伸ばされた平行六面体の体積を計算します


ここで、 Sは平行六面体の底面の面積です。 hは、このベースに描画される高さです。

基本面積は、簡単に計算されます-ベクトル積のモジュールとして


高さの決定では、いじくり回す必要があります。 角度を知っていたら あなたは簡単に高さを見つけるだろう


角度 三面角の線形および二面角に接続


三面角の最初の余弦定理です。 それから、二面角の余弦を表現します


結果のコサインを通して必要な角度のサインの二乗を表現します


Sと高さhを2乗することを忘れずに、（6）から（2）までの連続置換を実行します。 計算はかなりかさばるので、SKA（MapleまたはMathematica）を使用してそれらを取得し、平行六面体の体積の二乗を取得できます。


ここで、計量テンソルの行列式を計算します。 これは、行列の行列式と呼ばれ、テンソルの成分で構成されます。 その中に含まれる基底ベクトルのスカラー積を明示的な形式で書きます


計算すると、体積の2乗と同じ結果が得られます


したがって、ステートメント（1）は真です。 したがって、計量テンソルの行列式から根を抽出することにより、基底にまたがる平行六面体の体積を取得できます。


どこで 簡潔にするために、行列式の値を示します。

根（7）は、RTGのような一般相対性理論と重力の代替理論に関する文献によく見られます。 この値は基本的に重要であり、少し後で有用になります。

2.ベクトルのテンソル積。 ダイアド。 テンソルのランク。 畳み込み

スカラー積の式に注意してください

価値


2つのベクトルのテンソル積またはdyadと呼ばれます。 テンソルが乗算され、結果がテンソルになるため、この積はテンソルと呼ばれます。この場合は2番目のランクです。 。 テンソルのランクは、そのインデックスの数です。 ベクトルは、突然、テンソルでもあり、最初のランクのみです。 はい、これは理解できます-幾何学的エンティティとしてのベクトルは、考慮される座標系に依存しないためです。 そのコンポーネントのみが、座標系の選択に依存します。

もちろん、第2ランクのテンソル（8）は、その成分の行列で表されます


（8）を使用すると、スカラー積を次の形式で書き直すことができます。


これは、結果のテンソルのランクを下げるという事実のため、 畳み込みと呼ばれるテンソル積でもあります。 （10）のすべてのインデックスは「ダム」であり、メトリックテンソルとダイアドのコンポーネントを二重合計するために使用され、結果は数値cになります。

注意深い読者は、出力がテンソルであるべきだと言うでしょう。 したがって、テンソルはスカラーであることが判明し、テンソルでもあります。 インデックスがなく、基底を変更するときに変換できないため、ゼロランク。 スカラー積は基底変化に対して不変です。これは、スカラー積に含まれるベクトルの長さもベクトル間の角度も基底変化から変化しないためです。 したがって、スカラーはゼロランクテンソルです。

ただし、すべての数値がスカラーではありません。 スカラーは、ベクトルの長さ、ベクトルのスカラー積、物体の質量、絶対温度、および座標系に依存しない他の量です。 ベクトル成分はもはやスカラーではなく、基底が変化すると変化します。

テンソルのランクとコンポーネントのタイプについては少し後で説明しますが、今のところは次の燃え上がる質問に進みます。

3.ベクター製品。 Levi-Civitaテンソル

ベクトルに戻って、ベクトル乗算を実行しましょう


他のオプションがない場合、ブラケットを慎重に開き、操作の非可換性を記憶します




もちろん、私たちは大学でよく勉強し、それ自体のベクトルのベクトル積がゼロに等しいことを知っています。 しかし、単純化を急ぐことはありません。これは間違いなく楽しい事実に加えて、もう1つ、ダイアドのコンポーネント（9）が見えるからです。 しかし、ゼロ積に関連付けられた共線ベクトルの単純化を除けば、何も観察されなくなりました。 私たちは、その最も純粋な形で任意の基礎で作業します。

トリックを適用する-ベクトルを掛ける 最初の基底ベクトルに対するスカラー 今考えて



角括弧内の係数は、ベクトルの混合積です。 ベクトルが同一平面上にある（同じ平面にある）場合、そのような積はゼロに等しくなります。 つまり、混合製品で少なくとも1つのベクトルが繰り返される場合、ゼロに等しくなります。 したがって、9つの項のうち2つの項しかありません。これらの項では、混合乗算時にベクトルが繰り返されません。


だから、今それを覚えている -ベクトルの共変成分 。 最後に、最初の項のベクトル積のベクトルを再配置し、ベクトル積の規則に従ってマイナスを追加します


同様に、残りのコンポーネントを選択します



式（11）-（13）は、ベクトル積の混合からの因子まで、ベクトル代数のコースからベクトル積の射影を計算するための式を非常に連想させます。 しかし、我々はデカルトベースで作業しているわけではありません。何らかの違いを期待するのは自然です。 ところで、この乗数は何ですか？ 結局のところ、ベクトルの混合積は幾何学的な意味を持っています...それは同じです...それに含まれるベクトルがまたがる平行六面体の体積です。 そして、基底まで引き伸ばされた平行六面体の体積は、計量テンソルの行列式の根です！ それは


そのため、使用されたスペースのメトリックである表面化されました。 したがって、特定のテンソル、ベクトル積の結果である共変ベクトルを与える初期ベクトルの畳み込みを構築することが可能です。 さらに、このテンソルは計量テンソルに関連しています。 このような第3位のテンソルは、イタリアの数学者Levi-Civitaにちなんで名付けられました。

Levi-Civitaテンソルの成分が関係によって決定されることを確認するのは難しくありません


27個ありますが、それらのほとんど、つまり21はゼロに等しくなります。 これらは、インデックスが少なくとも1回繰り返されるコンポーネントです。 非ゼロのコンポーネントは6つのみで、非反復インデックスに対応しています。 モジュロは等しい しかし、そのうちの3つは正で、他の3つは負です。 式（11）-（13）では、ベクトルを所定の位置に再配置し、マイナスを追加してダイアドの係数を正にし、式自体はベクトル代数の過程に精通しているように見えます。 今、私たちはすべてをその場所に戻します




混合製品の符号は、インデックスの順序によって異なります。セット（1,2,3）、（2,3,1）、（3,1,2）では正、セット（1,3,2）、（2,1 、3）および（3,2,1）は負です。 ベクトルが正しい座標系で与えられている場合、それらの混合された積は、ベクトルが正しいトリプルを形成する場合、正になることが知られています。 最初の用語（16）-（18）では、基底ベクトルの正しいトリプルが現れます。 2番目の用語では、混合製品では同じベクトルが参加しますが、左のトリプルと見なされます。

どのトリプルが基底ベクトルを与えるかを決定する方法は？ 順序付けられており、番号1、2、3が割り当てられているため、非常に簡単です。ベクトルの順序に従うと、使用する座標系に対応するトリプル、つまり（1,2,3）-右のトリプルが得られます。

そして、最初にベクター2を取得した場合 次に、ベクトル3が順番に続きます。 そして次は何ですか？ そして、次のベクトル1、最初からやり直しますが、ベクトルの順序に違反することなく、つまり（2,3,1）-右のトリプル、および（3,1,2）-また右のトリプルに違反しません。 組み合わせ論の言語では、順序付けられたトリプルの基底ベクトルは、偶数の順列を形成します（つまり、要素のシーケンスに違反しません）。 トリプル内のトレースベクトルの順序が受け入れられたものと反対の場合、その順列は奇数になります。 したがって、順列（3,2,1）、（2,1,3）、（1,3,2）は奇数であり、ベクトルのトリプルは左利きです。

上記のすべてを使用して、関数を導入します


そして、（14）と（19）に基づいて、最終的にLevi-Civitaテンソルを書きます


正しい座標系のために


左座標系用。

その後、ベクトル積の式をテンソル形式で書き出すことができます


したがって、これはベクトル積であり、Levi-Civitaテンソルによるダイアドの畳み込みであり、出力コベクトル 、つまり共変成分によって定義されるベクトルを提供します。

4.ベクトルの混合（ベクトル-スカラー）積

習得した知識で武装して、私たちは今そのような操作を考えます


ベクトルを使用せずに、すぐにテンソル形式で記述しようとします。 まず、スカラー積は可換であるため、


ここで、スカラー積をテンソルとしてペイントできることを思い出してください
ベクトルカバー作業


（21）に基づいて、ベクトル積はコベクトルを与えるだけです。つまり、


つまり、最後に、テンソル形式の混合製品


ここで、Levi-Civitaテンソルが再び関与します。

式（22）は、ベクトルを操作することで取得できます。これも、Levi-Civitaテンソルの定義になりますが、ご覧のとおり、テンソル表記を使用する方が合理的です。

5.テンソルのランク。 共変成分と反変成分

したがって、ベクトル演算を分析する過程で、テンソルは、既知の多くの数学オブジェクトのプロパティと演算を一般化する数学オブジェクトであるという結論に達しました。 スカラーとベクトルは両方ともテンソルです。 それらは、共変成分と反変成分のランクと数が異なります。 ランクはテンソルインデックスの総数に等しく、括弧内の整数のペア（ p、q ）で示されます。ここで、 pは反変インデックスの数、 qは共変インデックスの数です。 テンソルはランクp + qの p倍反変、 q倍共変であると言われています。

1. ランクテンソル（0,0）はスカラーで、その値は単一の数値として表現でき、座標系の変化に対して不変の値を持ちます。 スカラーにはインデックスがなく、基底が変更されてもまったく変換されません。 ただし、すべての数値がスカラーではありません。 たとえば、ベクトルまたはテンソルの成分はスカラーではありません。基底が変化すると変化するためです。
   
2. ランクテンソル（1,0）はベクトルです。 ベクトルの場合、自然に反変な表現が必要です;ベクトルのスカラー積を計算するには、メトリックテンソルとの畳み込みが必要です。
   
   ベクトルのコンポーネントは、線形演算子を適用することによって変換されます。基本的には、ベクトルのコンポーネントを含む列を変換行列に乗算することにより、テンソル形式で表示されます
   
   
   
   
   
3. ランク（0,1）のテンソルはコベクトルです。 検討中の空間で非縮退計量テンソルが定義されている場合
   
   
   
   
   その場合、ベクトルとコベクトルは同じ幾何学的オブジェクトの2つの異なる表現、つまりベクトルです。 直交基底（ベクトルが相互に垂直である）では、反変座標と共変座標が一致します。 ある表現から別の表現への遷移は、メトリックテンソルとの畳み込みによって実行されます
   
   
   
   
   どこで 成分が行列である反変計量テンソル、
   逆行列テンソル成分 。
   
   ベクトルによるコベクトルのスカラー乗算では、メトリックテンソルを使用する必要はありません。ベクトルとの直接畳み込みによって生成されます。
   
   
   
   
   コベクトル成分の変換も線形演算子を適用して実行されますが、ベクトルとは異なり、コベクトル成分を含む行には座標変換行列が乗算されます
   
   
   
   
   
4. ランク（0,2）のテンソルは双線形形式であり、その例は2共変計量テンソルg _ijです。 メトリックテンソルのコンポーネントは、線形座標変換演算子を二重に適用することにより変換されます。これは、転置変換行列とメトリックテンソルの行列の乗算、および結果の変換行列との乗算に対応します。
   
   
   
   
   
5. ランクテンソル（2.0）-例はダイアド（8）です。 一般に、ランク（k、0）のすべてのテンソルはポリベクトルまたはポリアド （トライアド、 テトラッドなど）と呼ばれ、対応する数のベクトルのテンソル積の線形結合として形成されます。 それらの成分は、線形の適用量によって適切なランクに変換されます
   元のベクトルを変換する演算子。
   
6. ランク（1,1）のテンソルは線形演算子です。 例は、回転行列またはベクトルとコベクトルの他の座標変換です。 一般に、線形演算子の適用は、行列乗算の操作に還元されます。
   
   
   
   
   どこで -変換の結果。 -ソースベクトル。 線形演算子の行列のコンポーネントです。 線形演算子を変換するプロセスを検討してください。 Sをある基底から別の基底への遷移行列とする。 次に、基底を変更すると、両方のベクトルが変換されます-引数と結果の両方
   
   
   
   
   （24）を（23）に代入すると、
   
   
   
   
   ここで、左の行列を掛けます 私たちは得る
   
   
   
   
   どこで -マトリックス成分 。 一方、新しい基底のベクトルの場合、
   
   
   
   
   （25）と（26）を比較すると、線形演算子の変換式が得られます
   
   
   
   
   これらのオブジェクトにはすべて共通のプロパティがあります。コンポーネントのセットと、基底を変更するときの変換ルールがあります。
   

結論

結果の一部を要約します。

まず、ベクトル演算をテンソル関係に縮小できることを発見しました。これにより、エキゾチックな座標系を使用したり、空間の次元を増やしたりするたびに式を導出する不便さがなくなります。 関係は同じままで、空間のジオメトリに関連するテンソルの内部とその中での正の回転方向の選択のみが変更されます。 物理学、数学、力学の多くの方程式がベクトル量で動作することを考えると、テンソルを使用すると方程式を1回だけ書くことができます。 さらに、テンソルの記録はコンパクトです-それは計算を簡素化します。

第二に、多くの数学オブジェクト（スカラー、ベクトル、双線形形式、線形演算子）はすべてテンソルの特殊なケースであるため、より複雑な仲間のテンソルの強力な翼の下でプロパティを一般化できることを理解しています。

将来、テンソル表記法を使用して、共通の観点から非常に散文的な問題にアプローチし、研究者の生活を楽にする方法を検討します。

継続するには...