内容

はじめに

だから、私たちが理論的に長い間議論してきたことすべてを実践する時が来ました。このノートでは、主に以前の記事の資料を使用します。ここには、テンソルトピックに関する以前の出版物へのリンクがあります。

そして、我々は力学に従事します。テンソル計算を扱うようになったのは、力学の問題の解決策でした。そして、複雑な機械システムの運動を分析するために使用される第2種のラグランジュ方程式について説明します。これらの方程式の形式は、この分野のほとんどの専門家によく知られています

$\ frac {d} {dt} \ left（\ frac {\ partial T} {\ partial \ dot {q} ^ i} \ right）-\ frac {\ partial T} {\ partial q ^ i} = Q_i \ quad i = \上線{1、s}$

ここで、 sは機械システムの自由度の数です。 $q ^ i$ -一般化された座標; $T = T \左（\ vec {q}、\、\ dot {\ vec {q}} \右）$ -機械システムの運動エネルギー。 $Q ^ i$ -一般化された力。

これらの方程式に出くわした人は、運動エネルギーの三重微分を実行した後、一般化された座標の二次導関数の線形結合とその一次導関数の積の線形結合によって表される式が得られることに気づかなければなりません。そして、これは、少なくとも私にとっては、運動エネルギーを一般的な形で一度微分し、得られた一般的な式を使用して運動方程式を単純に構成できることを示唆しています。これを自分でやろうとしただけで、私は成功しませんでした。

それでも、一般にテンソル計算に依存している場合、運動エネルギーの微分に頼らずにこれを行うことができます（ただし、このアプローチも可能です）。とりあえずはこの記事でこれを行いますが、とりあえずは一点だけですが、同時に、検討中のアプローチの有効性を示すあまり複雑でない問題を解決します。

さあ、始めましょう！

1.任意の座標での質点の運動学

力学のプレゼンテーションの伝統は、点の動きを指定するベクトルの方法です

図 1.ポイントモーションを設定するベクトル方法

このモーション設定方法では、空間内のポイントの位置は、あるポイントOから解放された半径ベクトルによって決定されます。これは、参照ボディを意味します。この半径ベクトルは時間の関数です

$\ vec {r} = \ vec {r} \、（t）\ quad（1）$

関数（1）が与えられると、彼らは点の運動の法則が与えられると言います。点の運動の法則を知っていると、その速度と加速度を得ることができます

$\ vec {v} = \ frac {d \ vec {r}} {dt}、\ quad \ vec {a} = \ frac {d \ vec {v}} {dt} = \ frac {d ^ 2 \ vec {r}} {dt ^ 2} \ quad（2）$

半径ベクトル、速度、および加速度はベクトルです。つまり、これらをランク（1,0）のテンソルと見なします。さらに、デカルト座標系は使用しません。曲線座標を使用します

$q ^ i = q ^ i \、（t）\ quad i = \ overline {1、s} \ quad（3）$

どこで $q ^ i$ -空間内のポイントの位置を一意に特徴付ける一連の独立したパラメーター。そして、これらのパラメーターは必ずしも3つである必要はなく、それらのパラメーターの数が少ない場合もあります。すべてのパラメーターは、与えられたポイントの自由度に依存します。このような座標は、分析力学では一般化と呼ばれます。

自由度の数の決定は、2つの方法で定式化されます

物体の自由度の数は、空間内の物体の位置を一意に設定する従属座標の数nと、結合の物体rに課せられる方程式の数との差です。

$s = n-r$

空間内のポイントの位置を定義する座標の数はn = 3です。ポイントの移動が制約によって制限されていない場合、自由度の数も3になります。

ポイントが特定のサーフェスに沿って移動する場合、その移動は制限されます。サーフェスは、ポイントのデカルト座標に条件を課す接続です。この条件は、ポイントが移動する表面の方程式であり、通信方程式です。このような点の自由度の数はs = 2です。一般化された座標の数も2です。これらは、表面に沿ってカウントされる曲線座標です。

ポイントが特定の曲線に沿って移動する場合、2つの接続が既にその曲線に重ねられています。空間内の曲線は、2つのサーフェスの交線として定義されます。そのような点の自由度の数はs = 1であり、一般化された座標は1です—点が曲線に沿って通過した円弧の長さです。

したがって、座標（3）は、ポイントに重ねられた結合のジオメトリを自動的に考慮します。これにより、分析力学では、運動方程式から結合を除外できます。

自由度の数の別の定義は

物体の自由度の数-空間内の物体の位置を一意に決定する独立したパラメーターの数

関係の理解も含まれますが、よりベール化された形式です。

（3）点の運動の法則を呼び出します。運動の法則を知って、ポイントの速度と加速度のベクトルを取得します。時間の点の半径ベクトルを微分する

$\ vec {v} = \ frac {d \ vec {r}} {dt} = \ frac {\ partial \ vec {r}} {\ partial q ^ i} \、\ frac {dq ^ {\、i} } {dt} = \ frac {\ partial} {\ partial q ^ i} \ left（q ^ {\、j} \、\ vec {e} _j \ right）\ frac {dq ^ {\、i}} {dt} = \ frac {dq ^ {\、i}} {dt} \ vec {e} _i \ quad（4）$

（4）でアインシュタインのルールが機能し、式の右辺がミュートインデックスiおよびjで合計されることを思い出します。偏微分 $\ frac {\ partial} {\ partial q ^ i} \ left（q ^ {\、j} \、\ vec {e} _j \ right）= \ vec {e} _i$ 微分が発生するコンポーネントの係数です。式（4）は、曲線ベースでの速度ベクトルの展開です。

$\ドット{q} ^ {\、i} = \ frac {dq ^ {\、i}} {dt} \ quad（5）$

速度ベクトルには反変成分があります。ここで、加速度ベクトルを取得するために、時間で微分します（4）

$\ vec {a} = \ frac {d \ vec {v}} {dt} = \ frac {\ partial \ vec {v}} {\ partial q ^ {\、i}} \、\ dot {q} ^ {\、i} \ quad（5）$

前の記事の共変微分の定義を思い出し、一般化された座標に関する速度ベクトルの微分を書きます（前の出版物の式（33）を参照）

$\ frac {\ partial \ vec {v}} {\ partial q ^ {\、i}} = \ left（\ frac {\ partial \ dot {q} ^ {\、k}} {\ partial q ^ {\ 、i}} + \ Gamma_ {ji} ^ {k} \ dot {q} ^ {\、j} \右）\ vec {e} _k \ quad（6）$

どこで $\ Gamma_ {ji} ^ {k}$ -第2種のクリストッフェル記号

（6）を（5）に代入

$\ vec {a} = \ left（\ frac {\ partial \ dot {q} ^ {\、k}} {\ partial q ^ {\、i}} + \ Gamma_ {ji} ^ {k} \ dot { q} ^ {\、j} \右）\ dot {q} ^ {\、i} \、\ vec {e} _k = \ left（\ frac {\ partial \ dot {q} ^ {\、k} } {\ partial q ^ {\、i}} \、\ dot {q} ^ {\、i} + \ Gamma_ {ji} ^ {k} \、\ dot {q} ^ {\、j} \、 \ドット{q} ^ {\、i} \右）\、\ vec {e} _k \ quad（7）$

式（7）では、括弧内の最初の項

$\ frac {\ partial \ dot {q} ^ {\、q}} {\ partial q ^ {\、i}} \、\ dot {q} ^ {\、i} = \ ddot {q} ^ {\ 、k} \ quad（8）$

時間の一般化された座標の二次導関数。（8）を考慮して、最終的に点加速ベクトルの反変成分の式を書き留めます。

$a ^ k = \ ddot {q} ^ {\、k} + \ Gamma_ {ji} ^ {k} \、\ dot {q} ^ {\、j} \、\ dot {q} ^ {\、i }、\ quad（9）$

2.可能なポイント移動

定義することから始めましょう

可能（または運動学的に可能）なのは、ポイントに課された接続が侵害されないポイントのそのような動きです。

この概念は分析力学の基本です。非自由点の動きを考慮してください（図2）。ポイントをサーフェスに沿って移動させます。その座標は、軌道のすべてのポイントがこのサーフェス上にある値のみを取ることができます。このような座標は運動学的に可能と呼ばれ、それらは表面方程式によって相互接続されます。この場合、曲線座標を選択すると便利です $q ^ {\、i}$ 、ポイントが表面から離れないという事実を考慮します（結合をクリアするための条件を考慮しません）。上で述べたように、そのような座標は一般化と呼ばれます。

図 2.非自由点の可能な変位。

一般化された座標を変更します。つまり、座標の変化の法則に無限小関数を追加します。 $\デルタq ^ {\、i}$ 一般化座標のバリエーションと呼ばれる

$\チルダ{q} ^ {\、i} = q ^ {\、i} + \ delta q ^ {\、i} \ quad（10）$

ポイントがどのような動きをするかを計算します

$\ delta \ vec {r} = \ frac {\ partial \ vec {r}} {\ partial q ^ {\、i}} \、\ delta q ^ {\、i} = \ vec {e} _ {\ 、i} \、\ delta q ^ {\、i} \ quad（11）$

ベクトル $\デルタ\ vec {r}$ また、ポイントが移動する可能性があり、ポイントが移動する表面に接線方向に向けられます。（11）からわかるように、このベクトルは、一般化された座標のバリエーションである反変成分の観点から、ローカルベースに沿って分解されます。 $\デルタq ^ {\、i}$ 。一般化された座標は独立しているため、それらのバリエーションも独立しています。この事実は、将来的に私たちに役立つでしょう。

3.ポイントダイナミクスの一般方程式

図2に戻りましょう。非自由点は、結果が $\ vec {F} ^ {\、a}$ 。点は自由ではないため、結合の反応が適用され、その結果は $\ vec {R}$ 。ニュートンの第二法則と力の作用の独立の原理により、ベクトル方程式

$m \、\ vec {a} = \ vec {F} ^ {\、a} + \ vec {R} \ quad（12）$

点の可能な変位（11）をスカラーで乗算（12）

$m \、\ vec {a} \ cdot \ delta \ vec {r} = \ vec {F} ^ {\、a} \ cdot \ delta \ vec {r} + \ vec {R} \ cdot \ delta \ vec {r} \ quad（12）$

点に課せられた結合の理想性を想定します。つまり、それらの反応は点の可能な動きに作用しないことを意味します。

$\ vec {R} \ cdot \ delta \ vec {r} = 0 \ quad（14）$

原則として、これは常に許可されます。不完全な結合が存在する場合、特定の条件下でのそれらの反応は、アクティブな力のカテゴリに転送される可能性があり、タスクを複雑にしますが、基本的な困難ではありません。分析力学はこの仮定に基づいて動作します。同じように進み、正義（14）を入れて方程式に進みます

$m \、\ vec {a} \ cdot \ delta \ vec {r} = \ vec {F} ^ {\、a} \ cdot \ delta \ vec {r}$

ここで、関係（11）で提案されているように、一般化された座標（反復インデックスの合計を意味する）の変化によって可能な変位を拡張します。

$m \、（\ vec {a} \ cdot \ vec {e} _ {\、i}）\、\ delta q ^ {\、i} =（\ vec {F} ^ {\、a} \ cdot \ vec {e} _ {\、i}）\、\ delta q ^ {\、i} \ quad（15）$

式（15）の左側は、ポイントの加速度の共変射影であり、右側は、結果のアクティブな力の共変射影です。

$m \、a _ {\、i} \、\ delta q ^ {\、i} = Q _ {\、i} \、\ delta q ^ {\、i} \ quad（16）$

分析力学 $Q _ {\、i}$ 一般化されたアクティブな力と呼ばれます。（15）に基づいて、一般化された力は、結果のアクティブな力の共変成分であると結論付けます。

次に、（9）を計量テンソルで折りたたみ、（16）の結果を代入します

$m \、g_ {ij} \、\ left（\ ddot {q} ^ {\、j} + \ Gamma_ {kl} ^ {\、j} \、\ dot {q} ^ {\、k} \、 \ドット{q} ^ {\、l} \右）\、\ delta q ^ {\、i} = Q _ {\、i} \、\ delta q ^ {\、i} \ quad（17）$

一般化された座標の変化は独立しているため、係数はそれらと同一視でき、方程式のs （一般化された座標の数）を取得します。

$m \、g_ {ij} \、\ left（\ ddot {q} ^ {\、j} + \ Gamma_ {kl} ^ {\、j} \、\ dot {q} ^ {\、k} \、 \ドット{q} ^ {\、l} \右）= Q _ {\、i} \ quad i = \上線{1、s} \ quad（18）$

結果の方程式（18）を思い出させませんか？これは、第2種のラグランジュ方程式のすべての導関数を取得した後に得られる運動方程式に非常に似ています。さらに、これは2次のラグランジュ方程式です。運動エネルギーを微分し、速度ベクトルの反変成分で表現することで方程式（18）に到達できます。

同様に、第2種の分析方程式は、本質的に一般化された力で記述された一般的なダイナミクスの式である（15）に類似した式に基づいて分析力学で導出されます。さらに、式（15）は、その左辺と右辺がベクトルのスカラー積であるため、座標変換に関して不変です。そして、我々が思い出すように、スカラー積は基底の変化に関して不変です。

したがって、一般化された座標における質点の運動の微分方程式を取得しました。次に、それらを適用して、既知の問題を解決します。

4.中心力の作用下でのポイントの動き。ビネット方程式

引力/反発中心Oから放射状に向けられた力の作用下での平面内の重い点の動きを考えます。この問題は、中央フィールド内のポイントの動きの典型的な問題であり、単純な分析ソリューションを備えています。方程式（18）を使用してそれを解決し、それらを検証するのに十分なほど単純です

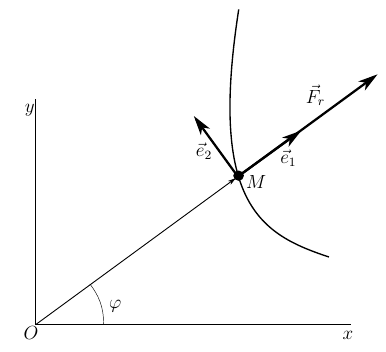
図 3.中央フィールド内のポイントの動き。

極座標で問題を解決します

$q ^ 1 = r、\クワッドq ^ 2 = \ varphi$

既知のメトリック（ここで確認できますが、取得できますが、非常に簡単です）

$\ mathbf {g} = \ begin {bmatrix} 1＆amp;＆amp; 0 \\ 0＆amp;＆amp; r ^ 2 \ end {bmatrix}$

極座標の場合、第2種のクリストッフェル記号を見つけることは難しくありません。それらのうち5つはゼロに等しく、3つだけがゼロ以外の値を持ちます。

$\ Gamma_ {22} ^ 1 = -r$

$\ Gamma_ {12} ^ 2 = \ Gamma_ {21} ^ 2 = \ frac {1} {r}$

これらのデータを使用して、方程式の左辺を書き出すことができます（18）

$m \、g_ {11} \左（\ ddot {q} ^ {\、1} + \ Gamma_ {22} ^ 1 \、（\ dot {q} ^ {\、2}）^ 2 \右）= m \左（\ ddot {r}-r \、\ dot {\ varphi} ^ 2 \右）$

$m \、g_ {21} \、\ left（\ ddot {q} ^ {\、1} + 2 \、\ Gamma_ {12} ^ 2 \、\ dot {q} ^ 1 \ dot {q} ^ 2 \右）+ m \、g_ {22} \、\左（\ ddot {q} ^ {\、2} + 2 \、\ Gamma_ {12} ^ 2 \、\ dot {q} ^ 1 \ dot { q} ^ 2 \右）= m \、r ^ 2 \、\左（\ ddot {\ varphi}-\ frac {2} {r} \、\ dot {r} \、\ dot {\ varphi} \右）$

力 $\ vec {F} _r$ 放射状に向けられており、考慮中の平面の任意の点でベクトルに沿って向けられます $\ vec {e} _1$ そしてベクトルに垂直 $\ vec {e} _1$ 、および一般化された力は、対応する基底ベクトルから生じるベクトルのスカラー積によって決定されるという事実に基づいて、次のように記述できます。

$Q_1 = F_r、\クワッドQ_2 = 0$

つまり、点の運動方程式を取得します

$\ ddot {r}-r \、\ dot {\ varphi} ^ 2 = \ frac {F_r} {m} \ quad（19）$

$r ^ 2 \、\ ddot {\ varphi}-2 \、r \、\ dot {r} \、\ dot {\ varphi} = 0 \ quad（20）$

式（20）は簡単に統合できます

$\ frac {d} {dt} \左（r ^ 2 \、\ドット{\ varphi} \右）= 0$

$r ^ 2 \、\ dot {\ varphi} = c \ quad（21）$

さらに、（21）はセクター速度の不変性を表します。これは中央フィールドの動きの特性です。（21）から、極角に関する微分を表現し、（19）に代入します。

$\ ddot {r}-\ frac {c ^ 2} {r ^ 3} = \ frac {F_r} {m} \ quad（22）$

（22）では、時間に関する微分から極角に関する微分に移ります。

$\ dot {r} = \ frac {dr} {d \ varphi} \、\ dot {\ varphi} = \ frac {c} {r ^ 2} \、\ frac {dr} {d \ varphi} = -c \、\ frac {d} {d \ varphi} \ left（\ frac {1} {r} \ right）\ quad（23）$

$\ ddot {r} = \ frac {d \ dot {r}} {d \ varphi} \、\ dot {\ varphi} = \ frac {c} {r ^ 2} \、\ frac {d \ dot {r }} {d \ varphi} =-\ frac {c ^ 2} {r ^ 2} \、\ frac {d ^ 2} {d \ varphi ^ 2} \左（\ frac {1} {r} \右）\クワッド（24）$

（24）を（22）に代入

$-\ frac {c ^ 2} {r ^ 2} \、\ frac {d ^ 2} {d \ varphi ^ 2} \左（\ frac {1} {r} \右）-\ frac {c ^ 2 } {r ^ 3} = \ frac {F_r} {m} \ quad（25）$

そして最後に、両側（25）に $-\ frac {r ^ 2} {c ^ 2}$ 私たちは得る

$\ frac {d ^ 2} {d \ varphi ^ 2} \左（\ frac {1} {r} \右）+ \ frac {1} {r} =-\ frac {F_r \、r ^ 2} { m \、c ^ 2} \ quad（25）$

この方程式は、中央フィールド内のポイントの運動に対するバイネット微分方程式として知られています。運動がニュートン重力の影響下で発生する場合、

$F_r =-G \、\ frac {m \、M} {r ^ 2}$

そして、一般的な解決策を次の形式で取得します

$\ frac {1} {r} = C_1 \ cos \ vaphi + C_2 \ sin \ varphi-\ frac {G \、M} {c ^ 2}$

これは、極座標の円錐曲線（円、楕円、放物線、双曲線）の方程式です

おわりに

この記事では、質点のダイナミクスに適用されるテンソル関係を使用するアプローチを示します。質点の動きは、任意の一般化された座標で記述できます。得られた方程式は、分析力学の一般原則に直接従い、2次ラグランジュ方程式と同等です。

このアプローチは、機械システムの動きの記述に適用できます。しかし、これについては少し後で説明しますが、今のところは、この作品を読んでくれた皆さんに感謝します。

継続するには...

テンソル代数の魔法：パート4-テンソルステートメントのポイントダイナミクス

内容

はじめに

1.任意の座標での質点の運動学

2.可能なポイント移動

3.ポイントダイナミクスの一般方程式

4.中心力の作用下でのポイントの動き。ビネット方程式

おわりに

More articles:

テンソル代数の魔法：パート4-テンソルステートメントのポイントダイナミクス

内容

はじめに

1.任意の座標での質点の運動学

2.可能なポイント移動

3.ポイントダイナミクスの一般方程式

4.中心力の作用下でのポイントの動き。 ビネット方程式

おわりに

More articles:

4.中心力の作用下でのポイントの動き。ビネット方程式