ジョルジア・フォーチュナの翻訳後投稿「 2 Pi or Not 2 Pi？ 」。
翻訳に協力してくれたキリル・グゼンコに深く感謝します。
3か月前、世界（または少なくともオタクの世界）はPi Day（03/03/15 ...）を祝いました。 今日（6/28-2015年6月28日）は別の数学的な日-日2π、または
タウ日 （2π= 6.28319 ...）です。
タウは実際に祝う日であり、πではなく
τ （=2π）が最も重要な定数であるべきだと言う人もいます。 それはすべて、2001年にユタ大学の数学者である
ボブ・ペールの有名なエッセイからの紹介から始まりました。
「一部の人はそれを冒aspと見なすことを知っていますが、πは間違いだと思います。」
これにより、一部のサークルではタウの日を祝いました-または、多くの人が言うように、2つのパイ（角）を食べることができる唯一の日（2pies≈2π-英語でしゃれ）。
しかし、
τがより良い定数であることは本当ですか？ 現代の世界では、これは非常に簡単に確認でき、
Wolfram言語はこのタスクをさらに簡単にします（実際、
番号piの
100周年記念日のスティーブン・ウォルフラムの投稿に触発され
た番号piの日付に関する Michael Trottの最近のブログ投稿は、Wolfram言語で非常に活発でした）。
arXiv.orgの 32万件のプレプリントを見て、実際に2πを含む数式の数と、他の要因を含むπまたはπを単に含む数式を比較しました。
以下は、2πを含む
WordCloud関数を使用して
作成されたいくつかの数式のクラウドです。
問題の数式の18％のみに2πが含まれていることがわかりました。これは、
τを使用するように切り替えることは適切な選択ではないことを意味します。
しかし、
τを使用する支持者は、なぜこの新しいシンボルの使用に進むべきだと信じているのでしょうか。 1つの理由は、
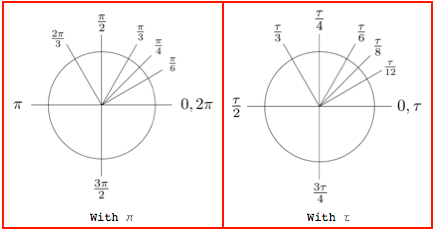
τを使用すると三角法の学習と理解が容易になるからです。 最後に、三角法では角度ではなくラジアンを使用し、円には2πラジアンが含まれます。 これは、円の4分の1が何かの4分の1ではなく、1/2πラジアンまたはπ/ 2に対応することを意味します！ この不正は、シンボル
τを導入することで排除でき、円の各部分は
τの同じ部分に対応します。 たとえば、1/4円は角度
τ / 4に対応します。
個人的に、私のπ数の使用は強い否定的な感情を引き起こさず、正直に言うと、
τを使用すると、三角法をより早く学ぶことができるとは思いません。 最も重要な2つの三角関数、サインとコサインを思い出しましょう。 おそらく、三角法の研究で最も重要な式は罪です
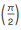
= cos（2π）= 1、およびsin（
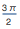
）= cos（π）= –1。 その値が覚えやすいので、常に余弦を使用することを好むだけでなく（πと2πに小数値がない）、常に1つの関数がπの倍数である点で非ゼロ値を取るという点で正弦と余弦が異なることも覚えています、他方はπの小数部分でゼロ以外の値を取ります。
τを使用すると、この対称性が失われ、sin
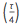
= cos（
τ ）= 1およびsin
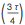
= cos
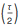
= –1。
上記を考えると、
τまたはπの使用は個人の好みの問題であることがわかります。 これは公正な結論ですが、どの定数がより有用であるかを判断するには、より厳密なアプローチが必要です。
最初に私が従ったアプローチでさえ、誤った結論につながる可能性があります。
タウのマニフェストで、マイケル・ハートルは
、しばしば2πを見つけることができる場所の例を挙げています。
実際、
τを使用すると、これらの式はすべて単純に見えます。 ただし、これらは科学者が定期的に使用する膨大な量の6つの公式であり、前述したように、2πを含む数式は多くありません。 それでも、2πを含まない式が
τを介して記述された場合、より単純になる可能性は十分にあります。 たとえば、式4π²は、単純にτ²と記述されます。
そこで、科学記事に戻って、2πの代わりに
τ （およびπの代わりに
τ / 2）を使用すると式が簡単になるかどうかを調べました。 たとえば、
τを使用するとより簡単になるものを次に示します。
そして、以下はそうではないものの一部です：
たとえば、よりシンプルな形式の記述で私が意味することを説明しましょう：
マニフェストのタウ式（上記参照）で表の左下の式にπを含む部分を取る場合：
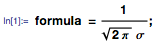ReplaceAll関数を使用してπを
τ / 2に置き換えて、以下を取得できます。
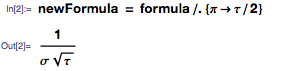
これら2つの式を見ると、2番目の式の方が簡単であることがわかります。 そして、ここでのポイントは直観ではありません-2番目では、単に文字が少なくなります。 明確にするために、
TreeForm関数を使用して、対応するツリーグラフを検討できます。
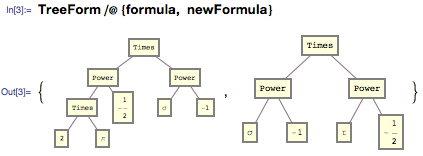
それらの差の数値表現を取得するために、元の式の文字数に対応する木の枝の数を使用できます。
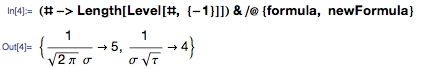τを使用した結果、式が単純化されるかどうかを判断するために、使用する定数（πまたは
τ）に応じて、記事からの式のπを含む各式（木の枝の数で決定）の複雑さを計算しました。 精度を高めるために、まず、πまたは2πに等しいまたは同等のすべての式を削除しました。 それらを考慮することは不公平だと感じました。なぜなら、それらはしばしば式の外で自分で発生するからです。 次に、
τを使用して式を単純化した場合と、複雑な場合の式を比較し、
τを使用して式の単純化が行われたのは43％のみでした。つまり、
τを使用すると式が複雑になります。 言い換えれば、この比較から、引き続きπを使用する必要があるということです。 しかし、これで話は終わりではありません。
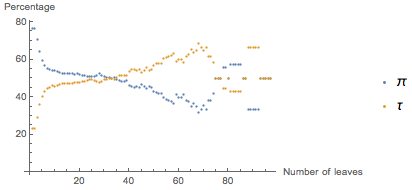
私はこれに気付きました：式が多少複雑になると、それが持っている分岐の数が40未満であることを意味します。実際、πまたは
τを使用すると簡単になる式の割合を見て、特定の値よりも少ない分岐の数を持っている場合、次の図が表示されます。
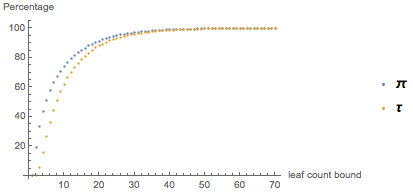x軸は、枝
の数の
上限を表します。 したがって、ほとんどすべての式では、分岐の数が50未満の場合にのみ、その複雑さはシンボルの選択に依存します。
より重要な観察結果は、式の複雑さが増すにつれて、状況が劇的に変化することです。 上記で考慮した式のように、複雑度が3を超える式を選択した場合でも
πを使用した方が簡単になるのは、
τの 52％に対して、式の48％だけです。 以下のグラフは、式の割合（πまたは
τを使用する方が簡単です）が複雑さによってどのように変化するかを示しています。
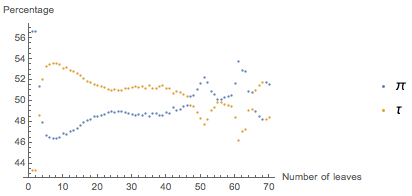
ご覧のとおり、ブランチの数が48を超えると、グラフィックはランダムに動作し始めます。 これは、サンプル式の0.4％のみが50を超える複雑さを持っているという事実の結果です。それらについて特に具体的なことは言えません。過去の経験から、これは本当に必要ないことがわかります。
また、このグラフから、日常生活の中で、次のようなものよりも複雑ないくつかの表現についてもわかります
、式を単純化するために、必ず
τを使用する必要があります。 しかし、もう触れていない点がもう1つあります。 さまざまなアプリケーション領域についてはどうですか？
おそらく、物理学では、式は
τで簡単に見えますが、他の領域ではそうではありません。 最初は、さまざまな分野の記事の検索に含めました。 ただし、πを含む式がいずれかの知識分野に属しているかどうか、または
τを使用してより簡単になる式が一部の限られたサブセットに属しているかどうかはチェックしませんでした。 実際、数学的記事のみを考慮すると、結果は次のようになります。
τを使用してより単純になるのは、すべての式の23％だけであり、それでもかなり複雑な式の場合のみです。 これは次のようなものです。
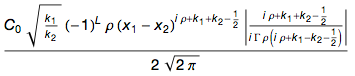τを使用して記述する方が簡単ですが、これらの式のほとんどは非常にまれです。 異なる分野の科学者は、それぞれの分野に固有の式に応じて異なる規則を使用するか、誰もが
τの使用に切り替える必要がありますが、実際には、これは一部の分野ではあまり意味がありません。 結局のところ、民主主義は大多数の満足を意味し、例外なく全員を満足させることは不可能です。
ただし、上記の式には、他に注目したいものが含まれています。
τに見える：
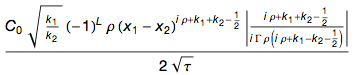τを使用して式を実際に簡単に記述できますが、このような改善はごくわずかであるため、無視できます。 たとえば、次の2つの式とそのブランチの数を考えてみましょう。
τの対応する式：
最初の式は
τでより単純ですが、ブランチの数は元の数よりも1/13だけ少なくなり、2番目の式はπで記述しやすくなり、置換後はその複雑さが1/6増加します。 つまり、最初のケースの改善は1/13で、2番目のケースでは-1/6でした（マイナス記号は劣化を意味します）。 ベクトルの平均値
は-0.044-負の数です。つまり、これら2つの式で
τを使用すると、ベクトル全体が0.044悪化します。
このようなベクトルアプローチは、方程式のサイズが考慮されていなかった以前に使用されたアプローチとは異なります。 単純化された式の数ではなく、改善点の数を考慮します。これにより、以前の結論が逆さまになります。 複雑さが以下に制限されている数式用にこれらのベクトルを取得しました-すべては前の例と同じです。 πを
τに置き換えるときの全体的な改善は、複雑さが増すにつれて減少することがわかります。
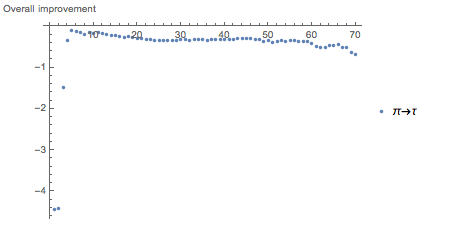
そして、最小の-0.04の劣化は難易度5で達成されます。ご覧のとおり、全体的な改善は常にマイナスです。 これは、より多くの数式でも
τの表記がより短いことを意味します（地域によって異なります）が、一般に、数式のすべての「単純化」の合計は、すべての「複雑さ」よりも重要です。
このすべての研究の結果として、私はこの立場を形成しました：私たちは古い友人πに満足し、
τの使用に切り替えるべきではないと思います。
最後に2つの発言があります。 1つは、
τがより積極的に使用される世界に住んでいた場合、結論は完全に反対になるということです。 式がすでに
τで記述されており、πの使用と単純化の問題への切り替えの問題を調査する場合、ベクトルの合計のグラフは次のようになります。
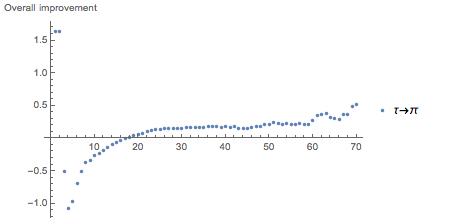
この違いは、グラフを構築するために使用されるベクトルが初期の困難に依存し、したがって変化すると変化するという事実によって説明されます。
複雑さが2より大きく18より小さいほとんどの式では、
τをπに置き換えることによる改善は負になります。 残念ながら、
τの支持者にとって、私たちはまだπの世界に住んでいます。
Michael Trottが私に指摘した2番目のポイントは、
Tauマニフェストの 2/3の式（投稿の冒頭の緑の表）に2πだけでなく、複雑な式2πiが含まれていること
です。 これはおそらく、私が答えようとしていた質問のポーズが間違っていることを示唆しています。 おそらく次の定式化の方が良いでしょう：複素数
2πiに新しい記号
τを導入するのは理にかなっていますか？
この新しい表記法では、πiをτ/ 2に置き換える必要もありますが、これはπiの複雑さに影響しません。 一般に、πiを含む数式は複雑さを軽減または保持します。 以下は、より単純になる数式のクラウドです。
そのため、彼らは
τを 2πiに置き換えた後、次のようになります。
式の改善率は十分に高くなく、2πiから
τへの移行
は不当であると主張することができます。 ただし、事実は逆のことです。πiを含むすべての式の75％はより簡単になり、残りの25％は複雑さのレベルを保持します。つまり、より複雑になる式はありません。 これは強力な議論ですが、私はこの考えを実装する立場にはありません。 しかし、等式
τ =2πi
は τ =2π
よりも有望である（そして歴史的に難しくない）と信じています。
τについてのあなたの意見がどうであれ、タウで素晴らしい一日を過ごしたことを願っています。 今日2つのpi（角）をお楽しみください。