繰り返しになりますが、C ++ 11標準の機能を使用してKaratsuba乗算を実装する方法に触れたいと思います。 このアルゴリズムはここで繰り返し検討されています(
「唐Kar法による長い数字の乗算」 、
「2つの数字を乗算する唐Kアルゴリズム」 )。必要なものではありません。
このハックされたトピックに飽きていない人、そしてこのシンプルだが非常に効果的なアルゴリズムを実装するのに苦労しているすべての人のために、読んでください。
目次
はじめに
私たちは皆、学校のコラムで乗算するように教えられました。 これは、何千年もの間知られている最も単純なアルゴリズムです。
アンドレイ・ニコラエヴィッチ・コルモゴロフでさえ1956年に仮説を立てた
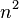
(次数の大きさによる乗算の下限で構成されていました
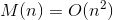
)、他のより高速なアルゴリズムがあれば、そのような非常に長い期間、それが見つかるからです。
単純な乗算の擬似コードは、メソッド自体のように単純です:
multiply(x[0 ... l], y[0 ... r]): res = [0 ... r+l] for (i = 0, i < r; ++i): carry = 0 for (j = 0, j < l; ++j): res[i + j] += carry + x[i] * y[j] carry = res[i + j] / base // base - res[i + j] %= base res[i + l] += carry
簡単にするために、パフォーマンスを支払う必要がある場合がありますが、このアルゴリズムは最適化でき、各ステップで残りを計算しません。
コルモゴロフ仮説の定式化の数年後、
アナトリー・アレクセーヴィチ・カラツバはより速い方法を発見しました。 彼のアプローチは、分割に一般化され、パラダイムを征服しました。 これがどのように機能するかを理解するために、2つの長さの数値を考慮

これを長さの2つの部分に分割します

:
![\\ X = \左[X_l \右] \左[X_r \右] = 10 ^ {\ frac {n} {2}} \ cdot X_l + X_r \\ Y = \左[Y_l \右] \左[ Y_r \ right] = 10 ^ {\ frac {n} {2}} \ cdot Y_l + Y_r](https://latex.codecogs.com/gif.latex?\\X&space;=&space;\left&space;[&space;X_l&space;\right&space;]\left&space;[&space;X_r&space;\right&space;]=10^{\frac{n}{2}}\cdot&space;X_l&space;+&space;X_r&space;\\Y&space;=&space;\left&space;[&space;Y_l&space;\right&space;]\left&space;[&space;Y_r&space;\right&space;]=10^{\frac{n}{2}}\cdot&space;Y_l&space;+&space;Y_r)
[1]:
\cdot\left(10^{\frac{n}{2}}\cdot&space;Y_l+Y_r\right)=\newline=10^n&space;X_l\cdot&space;Y_l+10^{\frac{n}{2}}\left(X_l\cdot&space;Y_r+X_r\cdot&space;Y_l\right)+X_r\cdot&space;Y_r)
4つの乗算を行う必要があり、複雑さは単純なアルゴリズムと変わらないことがわかります。 しかし、Anatoly Alekseevich Karatsubaは、長さの数字を3回掛けるとうまくいくと述べました。

-

、

、
\cdot&space;\left(&space;Y_l&space;+&space;Y_r&space;\right&space;))
。 確かに:
\cdot\left(Y_l&space;+&space;Y_r&space;\right&space;)&space;-&space;X_l\cdot&space;Y_l&space;-&space;X_r\cdot&space;Y_r)
4回ではなく3回の乗算で管理したため、カラツバアルゴリズムの動作時間は次の関係を満たします[2]。
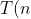=3T\left(\frac{n}{2}\right)+O(n))
、
最終的にはアルゴリズムの全体的な複雑さを与えます
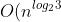)
。
Karatsuba乗算アルゴリズムの擬似コード:
Karatsuba_mul(X, Y):
そして、仕事のメカニズムを修正するための小さな数字の例:
a = 12 b = 81 res = Karatsuba_mul(a, b):
実装
これで、アルゴリズムをC ++で実装する準備が整いました。 インターネット上で、Cスタイルのコード記述を使用する実装をいくつか見つけました。これにより、初心者がコードを読むことが困難になります。 そのため、C ++ 11標準で利用可能な改善を可能な限り使用することにしました。 はい、これによりコードが遅くなりますが、ここでは主に理解と読みやすさの単純さに関心があります。
- 番号の保管。 C ++に精通しているすべての人が精通している標準整数ベクトルを使用します。 行の長い数値を読み取り、最後から選択したベースに対応するビットに分割します(先頭-10)。
たとえば、入力は数字を受け取りました:
123456789000000000
コンテナには次のように保存されます。
|0|1|2|3|4|5|...|n| 0 0 0 0 0 0 ... 1
Get_number()関数コード vector<int> get_number(istream& is) { string snum; vector<int> vnum;
- 番号を取得します。 入り口では、異なる長さの数字を受け取ることができます。アルゴリズムを正常に動作させるには、同じ長さの2の倍数にすることをお勧めします(「長い」数字を常に半分に分割するため) 関数extend_vec()を書いてみましょう。これは、ベクトルを受け取り、次のようにそれを長くします。
first = {4};
Extend_vec()関数コード void extend_vec(vector<int>& v, size_t len) { while (len & (len - 1)) { ++len; } v.resize(len); }
- 乗算 ここで、価値のあるいくつかの最適化について説明します。 残差をカウントせず、各再帰呼び出しで上位ビットに転送しますが、最後にこれを行います。 そして、たとえば128より短い長さで2つの数値を乗算するには、単純なアルゴリズムを使用します。これは唐津アルゴリズムよりも小さい定数であるためです。
機能コードnaive_mul() vector<int> naive_mul(const vector<int>& x, const vector<int>& y) { auto len = x.size(); vector<int> res(2 * len); for (auto i = 0; i < len; ++i) { for (auto j = 0; j < len; ++j) { res[i + j] += x[i] * y[j]; } } return res; }
機能コードkaratsuba_mul() vector<int> karatsuba_mul(const vector<int>& x, const vector<int>& y) { auto len = x.size(); vector<int> res(2 * len); if (len <= len_f_naive) { return naive_mul(x, y); } auto k = len / 2; vector<int> Xr {x.begin(), x.begin() + k}; vector<int> Xl {x.begin() + k, x.end()}; vector<int> Yr {y.begin(), y.begin() + k}; vector<int> Yl {y.begin() + k, y.end()}; vector<int> P1 = karatsuba_mul(Xl, Yl); vector<int> P2 = karatsuba_mul(Xr, Yr); vector<int> Xlr(k); vector<int> Ylr(k); for (int i = 0; i < k; ++i) { Xlr[i] = Xl[i] + Xr[i]; Ylr[i] = Yl[i] + Yr[i]; } vector<int> P3 = karatsuba_mul(Xlr, Ylr); for (auto i = 0; i < len; ++i) { P3[i] -= P2[i] + P1[i]; } for (auto i = 0; i < len; ++i) { res[i] = P2[i]; } for (auto i = len; i < 2 * len; ++i) { res[i] = P1[i - len]; } for (auto i = k; i < len + k; ++i) { res[i] += P3[i - k]; } return res; }
- 正規化 すべての転送を行うために残っており、結果を表示できます(または、さらに計算するために使用できます)。
機能コードfinalize() void finalize(vector<int>& res) { for (auto i = 0; i < res.size(); ++i) { res[i + 1] += res[i] / base; res[i] %= base; } }
そして、10より大きい基数を使用する場合はゼロで補完して結果を導き出します。
機能コードprint_res() void print_res(const vector<int>& v, ostream& os) { auto it = v.crbegin();
ナイーブアルゴリズムとカラツバアルゴリズムの速度の比較
テストプログラムをビルドするために、Clang ++に-O3スイッチを付けて使用しました。 10を底とする数値の表現のテスト結果を図1に示します。
製品の計算時間(基数10)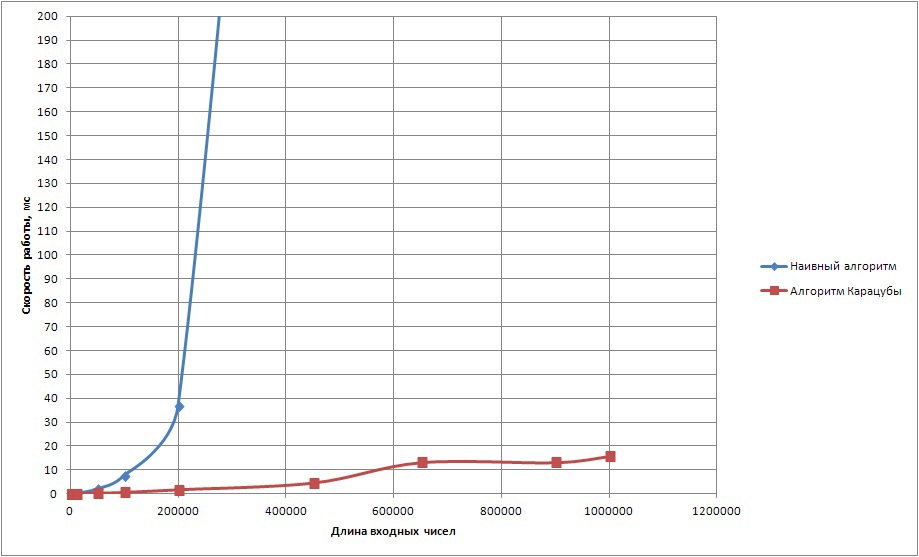 図1. 10を基数とするビューを使用した2つの数値の積の計算時間
図1. 10を基数とするビューを使用した2つの数値の積の計算時間 単純なアルゴリズムは、長さが長い入力数値では大幅に遅くなることがわかります。
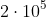
。
図2は、同じアルゴリズムの結果を示していますが、最適化はほとんど行われていません。 これで、100を基数として長い数字がベクターに配置され、生産性が大幅に向上します。
製品の計算時間(ベース100)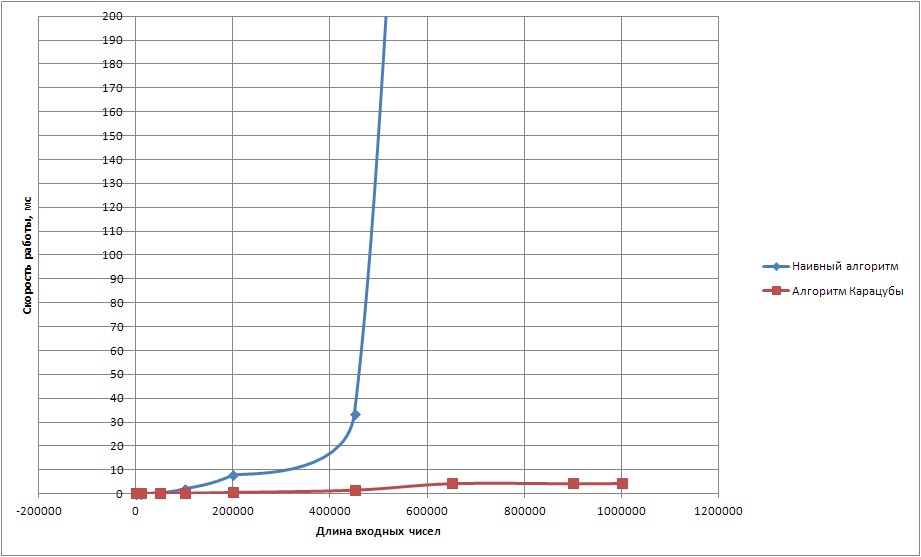 図2.基数が100のビューを使用した2つの数値の積の計算時間
図2.基数が100のビューを使用した2つの数値の積の計算時間 結論
以上で、この簡単で効果的な乗算方法を整理しました。 この資料が役に立つことを願っています。アルゴリズムを勉強し始めたばかりの多くの初心者がもうlonger迷に陥らないことを願っています(まあ、彼は私に一度も行ったことはありません)。
この実装を最適化することはまだたくさんあります。
- ベクトル内の数値が格納されるベースを増やします。 これで、数値の正規化が最後に行われ、C ++で標準型のオーバーフローが発生します。 unsigned long long型の配列/ベクトルに数値を保存し、乗算の各段階で残りをハイフンで計算する価値があるかもしれません。 または、残りの「長い」表現を使用します。
- 配列を優先してベクトルを破棄し、イテレータを使用して数値の左右の部分の割り当てを使用しないでください。
それだけです、ご清聴ありがとうございました。
記事を書くときに使用された元のプロジェクトは
こちらです。
使用された文献のリスト
- S.ダスグプタアルゴリズム:A. S.クリコフ編集によるA. S.クリコフによる英語からの翻訳[テキスト] / S.ダスグプタ、H。パパディミトリウ、U。ワジラニ -モスクワ:ICMMO、2014-320 p。
- Karatsubaアルゴリズム[電子リソース] / Wikipedia-URL: en.wikipedia.org/wiki/Karatsuba_algorithm
- A. S. Kulikovアルゴリズムとデータ構造[電子リソース] / A. S. Kulikov-URL: https ://stepic.org/course/Algorithms- and data structures-63 / syllabus