内容

はじめに

剛体の角速度テンソルを取得することを約束し、最終回転のパラメーターの観点から表現することを約束したので、時間の順序によってすでにリークしています。 KDPVを見ると、なぜこれほど長い間考えていたのかが明らかになります。テーブル上の紙の束が私の思考の流れです。

テンソル式の変換はまだ楽しいです...

残酷なテンソルは単純化したくありませんでした。むしろ、彼らはそれを望んでいましたが、変換中に、不注意のために括弧が開くと、小さなエラーが発生し、全体像を見ることができませんでした。その結果、結果が得られました。これにおける最後の役割は、主にEugeneKalentevの記事のおかげで、私が頼ったSKA Maximaによって果たされたわけではありません。この記事の重点は、特定のデータ構造で表されるテンソルを使用した計算作業にシフトしました。抽象テンソルを扱う問題に興味がありました。 Maximaがそれらを使用できることが判明しましたが、それは望んでいる方法ではありませんが、それでも私の人生を大幅に簡素化しました。

したがって、ソリッドのメカニズムに戻り、同時にMaximaでテンソルを使用する方法を確認します。

1.回転テンソルの最終的な表現について少し

前回の記事で、Levi-Civitaテンソルの積の畳み込みの原理を研究した私たちは、回転テンソルのこの表現を得ました。

$B_k ^ {\、m} = u ^ {\、m} \、g_ {jk} \、u ^ {\、j}-\ cos \ varphi \、\ left（\ delta_ {j} ^ {\、m } \、\ delta_ {k} ^ {\、q}-\ delta_ {k} ^ {\、m} \、\ delta_ {j} ^ {\、q} \右）\、u_ {q} \、 u ^ j + \ sin \ varphi \、g ^ {mi} \、U_ {ik} \ right \ quad（1）$

まだ簡略化できます。このため、2番目の用語の括弧内の式を使用します

$\左（\ delta_ {j} ^ {\、m} \、\ delta_ {k} ^ {\、q}-\ delta_ {k} ^ {\、m} \、\ delta_ {j} ^ {\、 q} \右）\、u_ {q} \、u ^ j = \ delta_ {j} ^ {\、m} \、\ delta_ {k} ^ {\、q} \、u_ {q} \、u ^ j-\ delta_ {k} ^ {\、m} \、\ delta_ {j} ^ {\、q} \、u_ {q} \、u ^ j =$

$= u ^ m \、u_ {k}-\ delta_ {k} ^ {\、m} \、u ^ q \、u_ {q} = u ^ m \、u_ {k}-\ delta_ {k} ^ {\、m} \ quad（2）$

なぜなら、たとえばテンソルとクロネッカーデルタの畳み込みにより、サイレントテンソルインデックスがクロネッカーデルタのフリーインデックスに置き換えられるためです。 $\ delta_ {k} ^ {\、q} \、u_ {q} = u_ {k}$ 。このように行動し、ベクトル $\ vec {u}$ 長さが1に等しい。これは畳み込みを意味する $u ^ {q} \、u_ {q} = 1$ 、（2）を取得します。回転テンソルの式はさらに単純に見えます

$B_k ^ {\、m} = \左（1-\ cos \ varphi \右）u ^ {\、m} \、u _ {\、k} + \ cos \ varphi \、\ delta_ {k} ^ {\ 、m} + \ sin \ varphi \、g ^ {mi} \、U_ {ik} \ right \ quad（3）$

第7回の記事で推測するために長くて退屈な試みのために試みたまさに表現。途中で何も研究できないというルールをもう一度確認します...

なぜ私はこれをすべてしたのですか？最初に、最終的に読者の目にリハビリをすること。第二に-結果を比較するために、Maximaで少し低くなる結果が得られるようにします。そして第三に、表現（3）で私たちの甘い生活が終わり、巨大な変容の地獄が始まると言うことです。

2. Maximaを使用して角速度テンソルを導出します

itensorモジュールは、Maximaの抽象テンソル、元のドキュメント、ロシア語に翻訳されたドキュメント、およびドキュメントに基づいた別の本で作業する責任があります。

少なくともコンソールで、少なくともグラフィックフロントエンドの1つを使用してMaximaを起動し、

 kill(all); load(itensor); imetric(g); idim(3);

ここでは、メモリを消去し（ kill()関数）、すべての定義とロードされたモジュールを削除し、 itensorパッケージをロードします（ load()関数）、メトリックテンソルはg （ imetric()関数）と呼ばれ、また、空間の次元（ idim()関数）を指定します。これは、SKAがデフォルトでリーマンメトリックの4次元時空で機能すると見なすためです。古典力学の3次元空間で作業しており、メトリックはねじれのない非縮退です。

回転テンソルを紹介します

 B:ishow( u([],[l])*g([j,k],[])*u([],[j]) - cos(phi)*'levi_civita([],[l,q,i])*u([q],[])*'levi_civita([i,j,k],[])*u([],[j]) + sin(phi)*g([],[l,i])*'levi_civita([i,j,k])*u([],[j]))$

itensorテンソルは識別子によって宣言されます。その後、共変および反変のインデックスのリストは、コンマ付きの括弧で示されます。 levi_civita()関数は、Levi-Civitaテンソルを定義し、その前の素数は、このテンソルを計算する必要がないことを意味します。 Maximaは、可能であれば式を計算および単純化する方法で知られています。ストロークが入力されない場合、Levi-Civitaテンソルは「カボチャ」に変わり、具体的には、計画に含まれていない一般化クロネッカーデルタを介してそれを決定しようとします。

$文字はセミコロンの代替であり、変換結果の表示を禁止します。 ishow()を使用して情報を表示します。代入された式は、テンソルレコードの通常のインデックス表記で画面に表示されます。画面では次のようになります

さらに、反対称テンソルを導入せずに、その単純化されていない形式を二重ベクトル積で導入します $\ mathbf {U}$ 最初の段階で（3）を取得し、マシンがテンソル式をどのように単純化するかを確認するため。人間的には、この表現は次のようになります

$g_ {j \、k} \、u ^ {l + j}-\ varepsilon_ {i \、j \、k} \、\ cos \ Phi \、\ varepsilon ^ {i \、l \、q} \、 u_ {q} \、u ^ {j} + g ^ {i \、l} \、\ varepsilon_ {i \、j \、k} \、\ sin \ Phi \、u ^ {j}$

ただし、最初の項のインデックスの合計は、私たちには未知の特別な魔法の疑いを示唆しています。しかし、この結論は、呪文を使用してマキシマによって直接生成されます

 load(tentex); tentex(B);

これにより、LaTeXコードの形式で出力を取得できます。欠点の中で-インデックスと回転角度を示す大文字のシャーマニズム、両方とも原則的に修正可能ですが、MaximaはTeX出力がMapleほど冗長ではないという事実に満足しています。

どうぞ次に、回転テンソルを介して角速度を決定する式を思い出します

$\ Omega _ {\、mk} = g _ {\、mp} \、B_ {l} ^ {'\、p} \、\ dot {B} _ {k} ^ {\、l} \ quad（4）$

ここで、時間に関して（3）を微分し、導関数に逆行列（3）と計量テンソルを掛ける必要があると想像してください。これは手動で行うことができますが、このプロセスを終了すると、テーブル上のシートのスタックは3倍厚くなります。

まず、導入された回転テンソルを単純化します

 B:ishow(expand(lc2kdt(B)))$

lc2kdt()関数は、Levi-Civitaテンソルを含む式を単純化するために特別に設計されています。彼女はこのテンソルを可能な限り崩壊させ、クロネッカーデルタの和と積の組み合わせを出力に与えようとします。結果は次のようになります

括弧を展開する関数expand() 、 lc2kdt()結果にも適用されます。これがないと、Maximaはたぶん畳み込みを実行します。

それでは、畳み込みを実行して、結果の式を計算してみましょう。 contract()関数は、畳み込みを実行する最も信頼できる方法の1つです。

 B01:ishow(contract(B))$

出力を取得します（可能な場合、 tentex()関数を使用してMaximaによって生成されたLaTeX出力を引用します）

$\ delta_ {k} ^ {l} \、\ cos \ Phi \、u_ {q} \、u ^ {q} -u_ {k} \、\ cos \ Phi \、u ^ {l} + u_ {k } \、u ^ {l} + g ^ {i \、l} \、\ varepsilon_ {i \、j \、k} \、\ sin \ Phi \、u ^ {j}$

これは式（3）に似ています。これにより、プログラムの正しさと自分の行動の正しさを確信しました。だから、先に進むことができます。

Maximaが考慮しない唯一のことは、回転が行われるベクトルの長さが1に等しいことです。したがって、彼は表現を崩壊させません $u ^ {q} \、u_ {q}$ スカラーへ。注意深く検索しましたが、どうして彼にこのことを伝えることができなかったのでしょうか。将来的には、これは深刻な困難をもたらしますが、これについてはお話ししますが、今のところは松葉杖で出て、不快なテンソルをユニットに置き換えました

 B01:ishow(subst(1, u([],[q]), B01))$ B01:ishow(subst(1, u([q],[]), B01))$

最終的な回転のパラメータに関する回転テンソルの表現には、逆行列を取得することで（3）の反対の符号で回転角度を置き換えることになるという快適な特性があります。確かに、他の方向への転換は逆変換です。これは、回転行列の特性に基づいて、厳密に数学的に証明できます。私はこれを行っており、この記事では不要なリードだと考えています。逆テンソルを取得するだけです

 B10:ishow(subst(-phi, phi, B01))$

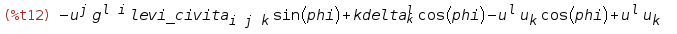
導関数を取得するので、Maximaはどのテンソルと数値パラメーターが時間に依存するかを知る必要があります。回転軸の方向と回転角度は時間に依存することを示します

 depends([u,phi], t);

テンソルが式（4）に対応するように、インデックスの名前を変更します

 B10:ishow(subst(p,l,B10))$ B10:ishow(subst(l,k,B10))$ B10:ishow(subst(i1,i,B10))$ B10:ishow(subst(j1,j,B10))$ B10:ishow(subst(s,q,B10))$

したがって、（4）での正しい乗算のために、フリーインデックスの名前を変更し、サイレントインデックスの名前を再定義しました。規則によれば、乗算されたテンソルのサイレントインデックスの名前は一致しないと想定されています。

ここで、回転テンソルの時間微分を取ります

 dBdt:ishow(diff(B01,t))$

出る

差別化が正しく実行されたことを確認します。最後に、式（4）を導入し、Levi-Civitaテンソルを考慮して、括弧の開きと単純化を順次適用します

 exp1:ishow(lc2kdt(expand(g([m,p],[])*B10*dBdt)))$

結果は表示するのが怖いですが、もしあなたが

この混乱の中で何かを理解することは困難です。しかし、 %後の数字を含むダムインデックスの奇妙な指定で、クロネッカーデルタの組み合わせ（ kdelta()関数が任意のランクのクロネッカーデルタを設定するkdelta()が出たことは明らかです。事実は、Maximaが変換するとき、愚かなインデックスを数えるということです。これをすべて単純化してみましょう

まず、もう一度、Levi-Civitaテンソル（ lc2kdt() ）を考慮に入れた単純化を通して式を実行してみましょう。次に、畳み込みを行います（ contract() ）。その後、 canform()関数を適用して「ワニ」の単純化を試みます。これにより、サイレントインデックスが列挙され、テンソルが単純化されます。この機能は、単純化のために開発者によって推奨されています。

 exp2:ishow(canform(contract(lc2kdt(exp1))))$

その結果、「ワニ」の深刻な体重減少が観察されます

しかし！最初の項では、それ自体の回転軸の単位ベクトルのベクトル積が見られ、ゼロでなければなりません。 Maximaはこれをまだ理解していないため、このような単純化の可能性を指摘する必要があります。私たちはそれを構造にします

 exp3:ishow(canform(contract(expand(applyb1(exp2,lc_l,lc_u)))))$

applyb1()関数は、単純化された式に含まれる部分式を単純化するためのルールを設定します。式とルールのリストが引数として渡されます。 2つのルールがあります： lc_lおよびlc_u下位（ lc_l ）および上位（ lc_u ）インデックスを持つLevi-Civitaシンボルを持つ部分式を変換するためのルール。同時に、部分式の変換後に表示されるブラケットを再度開き、畳み込みと単純化を実行します。その結果、ワニの質量の別の減少が観察されます

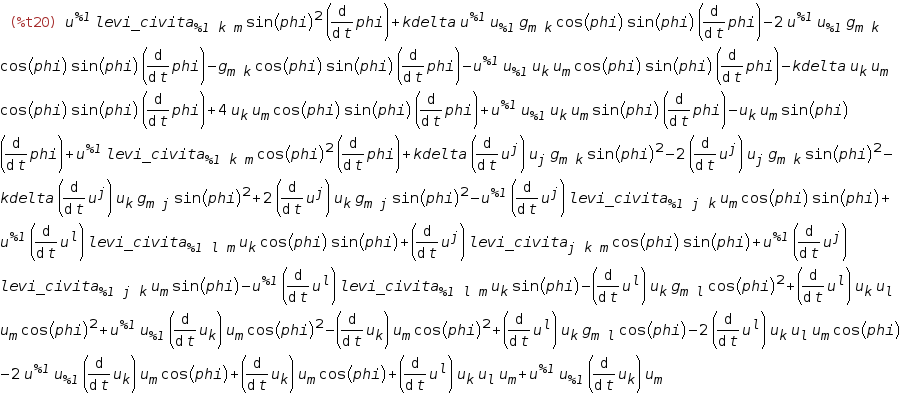
おそらくこれは制限ではありません。しかし、おそらく無知と経験不足に驚いた。

kdelta変数に注意してkdelta 。 Maximaでの実験により、これがランク2のクロネッカーデルタのトレースであり、空間の次元（単一行列のトレース）に等しいことがわかりました。私たちの場合、これは数字の「3」です。 kdelta代わりに立つべき3つです。しかし、何らかの理由で価値がない場合は、テンソルパッケージの構成変数が何らかの形で誤って構成されている可能性があります。 kdeltaを3にすると、さまざまな類似した類似の用語の束が形成され、合計でゼロになります。
すべてのビューの畳み込み
$u ^ {i} \、u_ {i}$

これは回転単位の単位ですが、変化せず、1に等しくなります。私にとってMaximaについてこれを言う方法はまだ明確にされていません。
それは前の問題から流れます
$u ^ i \、u_i = 1$

つまり

$\ dot u ^ {i} \、u_ {i} + u ^ {i} \、\ dot u_ {i} = 0＆quot;$

そこから、スカラー乗算演算の可換性により、

$\ dot u ^ {i} \、u_ {i} = 0、\ quad u ^ {i} \、\ dot u_ {i} = 0＆quot;$

上記の結果には、最近の表現がよく見られます。

これらの問題を知っている人々の助けに非常に感謝します。ドキュメントの研究は解決策にまだ光を当てていないからです。 subst()置換関数はここでは機能しません。

この点で、私は再びペンと紙を取り上げて角速度テンソルを「単純化」しました。しかし、マキシマは私のためにタスクを大いに促進しました。

3.ペン、紙、ファイル、タンバリンの使用...

ゼロ以外のすべての用語を書き、同様の用語を提示し、共通の要素を角かっこから取り出します。驚くべきことに、すべてが美しく、すばやく式に崩れます

$\ Omega _ {\、km} = \左（1-\ cos \ varphi \右）\左（\ dot u _ {\、k} \、u _ {\、m}-u _ {\、k} \、\ dot u _ {\、m} \ right）+ \ sin \ varphi \、\ left（1-\ cos \ varphi \ right）\、u ^ {\、i} \ left（\ varepsilon _ {\、ijk} \、\ドットu ^ {\、j} \、u _ {\、m}-\ varepsilon _ {\、ilm} \、\ dot u ^ {\、l} \、u _ {\、k} \右）+$

$+ \ sin \ varphi \ cos \ varphi \、\ dot u ^ {\、j} \ varepsilon _ {\、jkm} + \ dot \ varphi \、\ varepsilon _ {\、ikm} \、u ^ {i} \ quad （5）$

この式は、直交ベースで取得され、行列形式で表される式に似ています。

Pogorelov D. Yu。身体システムのダイナミクスのモデリング入門。 ページ 31。

テンソル（5）は非対称で、インデックスを再配置し、対応する式の符号を変更します。最初の項は共変テンソル積の差であり、2番目は転置された最初であり、そのような合計は出力に反対称テンソルを与えます。残りの項にはLevi-Civitaテンソルが含まれており、インデックスを再配置すると符号が変わります

$\ Omega _ {\、mk} = \ left（1-\ cos \ varphi \ right）\ left（\ dot u _ {\、m} \、u _ {\、k}-u _ {\、m} \、\ dot u _ {\、k} \右）+ \ sin \ varphi \、\左（1-\ cos \ varphi \右）\、u ^ {\、i} \左（\ varepsilon _ {\、ilk} \、\ドットu ^ {\、l} \、u _ {\、m}-\ varepsilon _ {\、ijm} \、\ dot u ^ {\、j} \、u _ {\、k} \右）+$

$-\ sin \ varphi \ cos \ varphi \、\ dot u ^ {\、j} \ varepsilon _ {\、jmk}-\ dot \ varphi \、\ varepsilon _ {\、imk} \、u ^ {i}$

繰り返しますが、最後の2つの用語のインデックスを再配置します

$+ \ sin \ varphi \ cos \ varphi \、\ varepsilon _ {\、mjk} \、\ dot u ^ {\、j} + \ dot \ varphi \、\ varepsilon _ {\、mik} \、u ^ {i} \クワッド（6）$

そのため、その畳み込みは、行列積でのベクトル積の表現に馴染みのあるスキュー対称行列を生成します。

デカルト基底を受け入れれば、さらに（6）の単純化が可能です。次に、共変成分と反変成分が一致し、Levi-Chevitaテンソルの非ゼロ要素がモジュロになり、（6）をさらに簡略化できます。しかし、この式は任意の基準で取得しました。

おわりに

それで、Maximaテンソルツールのおかげで、最終的な回転のパラメーターを使用して角速度テンソルを表現するタスクがようやくわかりました。同時に彼は、SKAでテンソルを使用した実例を読者に示しました。

次回、（6）から角速度と角加速度の擬似ベクトルを取得し、固体の運動学のテンソル記述に近づきます。

ご清聴ありがとうございました！

継続するには...

テンソル代数の魔法：パート9-最終回転のパラメーターによる角速度テンソルの導出。マキシマを適用

内容

はじめに

1.回転テンソルの最終的な表現について少し

2. Maximaを使用して角速度テンソルを導出します

3.ペン、紙、ファイル、タンバリンの使用...

おわりに

More articles:

テンソル代数の魔法：パート9-最終回転のパラメーターによる角速度テンソルの導出。 マキシマを適用

内容

はじめに

1.回転テンソルの最終的な表現について少し

2. Maximaを使用して角速度テンソルを導出します

3.ペン、紙、ファイル、タンバリンの使用...

おわりに

More articles:

テンソル代数の魔法：パート9-最終回転のパラメーターによる角速度テンソルの導出。マキシマを適用