内容

1. テンソルとは何ですか、なぜ必要ですか？
2. ベクトル演算とテンソル演算。 テンソルランク
3. 曲線座標
4. テンソル博覧会のポイントのダイナミクス
5. テンソルのアクションとその他の理論的な質問
6. 自由固体の運動学。 角速度の性質
7. ソリッドの最終回転。 回転テンソルのプロパティとその計算方法
8. Levi-Civitaテンソルの畳み込みについて
9. 最終回転のパラメーターによる角速度テンソルの導出。 頭とマキシマを適用
10. 角速度ベクトルを取得します。 欠点に取り組む
11. 自由な動きでの体のポイントの加速。 ソリッドの角加速度
12. 固体運動学におけるロドリゲハミルトンパラメーター
13. テンソル式の変換の問題におけるSKA Maxima。 ロドリゲ・ハミルトンのパラメーターにおける角速度と加速度
14. 剛体のダイナミクスの非標準的な紹介
15. 非自由な固体運動
16. 固体の慣性テンソルの特性
17. ナットジャニベコバのスケッチ
18. ヤニベコフ効果の数学的モデリング

はじめに

この記事では、2つの問題を解決します。 前の記事で計画したよりも詳細に議論したロドリゲハミルトンパラメーターを通じて角速度と角加速度の式を取得します。 同時に、この目的のためにオープンマキシマSKAを使用する方法をデモンストレーションします。これは、判明したように、テンソルにうまく対処します。特定のスキルがあれば、科学的問題を解決する上で深刻な助けになります。 私にとって、Maximaは新製品です。それ以前は、Mapleで、そしてMathematicaでかなり働いていました。 したがって、おそらく私が使用するいくつかのトリックは、専門家ではないように見えるかもしれません。


SKAは私たちを助ける準備ができており、合理的なチームを待っています...


前回は、四元数代数を使用して回転変換を表現する方法を示すことに焦点を当てました。 ユニットによって指定された回転軸の方向を知る 座標系を回転させる角度 コンポーネントにユニットクォータニオンを構築できます

そして、ベクトルの回転の直接変換 乗算クォータニオンに減少

および逆変換

ベクトルに対して実行される変換（2）および（3）は、最終回転を記述するロドリゲ公式を直接与えることを示しました。 ここでの目標は、回転四元数パラメーターを回転テンソルと角速度および角加速度の擬似ベクトルに接続することです。

1.ロドリゲ・ハミルトンのパラメーターにおける回転テンソル

回転テンソルの式はすでによく知っています。



四元数を導入し、そのベクトル部分を反変成分として提示します



この場合、（5）から（4）への置換は手動で行うことができ、このプロセスには特別なことは含まれません。 しかし、Maximaですべてを行うと同時に、さらなる作業のためにいくつかの初期データを準備します。 3次元空間のテンソルで動作するようにMaximaを構成します

/*   */ kill(all); /*         LaTeX  */ load(itensor); load(tentex); /*         */ imetric(g); idim(3); 

回転テンソルの式（4）を紹介します

 B:ishow(2*sin(phi/2)^2*u([],[m])*u([k],[]) + (cos(phi/2)^2 - sin(phi/2)^2)*kdelta([k],[m]) + 2*sin(phi/2)*cos(phi/2)*g([],[m,i])*'levi_civita([i,j,k],[])*u([],[j]))$ 

ニュアンスに注意してください-半分の角に移動しました。 それ以外の場合、三角法を単純化しようとすると、Maximaは何も単純化せず、半引数式の計算を含むhalfanglesフラグを設定してもhalfanglesません。 これは私が適用しなければならなかった最初の松葉杖です。 おそらく無知から。

最終回転のパラメーターと四元数の成分の関係を設定します

 Lambda0:p0 = cos(phi/2); Lambda:ishow(p([],[j]) = sin(phi/2)*u([],[j]))$ 

ここでは、簡潔にするために（毎回lambdaを入力するための怠laz）、四元数の成分は文字p示されます。

四元数のベクトル部分を通して回転軸の単位ベクトルを表現します

 Solv1:ishow(solve(Lambda, u([],[j])))$ 

式の配列の形式で方程式の解を出力で受け取る



得られた式では、回転テンソルには回転単位ベクトルの共変成分が含まれているため、インデックスを省略する必要があります。 これを行うには、この前に取得した式をメトリックテンソルで折りたたみます

 u_k:ishow(contract(Solv1[1]*g([k,j],[])))$ 

さらに、共変成分のインデックスjをmに置き換えます

 um:ishow(subst(m, j, Solv1[1]))$ 

その結果、回転テンソルへの置換の準備ができた2つの式を取得します。



これで、回転軸のorthコンポーネントを回転テンソルの式に置き換えることができます。 この場合のステージング関数subst()は2つの引数を取ります。2番目の引数に付属する式に置き換える必要がある式です。 この場合、最初の引数の左部分が変換された式で検索され、その右部分に置き換えられます

 B_1:ishow(subst(u_k, B))$ B_1:ishow(subst(um, B_1))$ B_1:ishow(subst(Solv1[1], B_1))$ 

出口には



さて、四元数のベクトル部分のコンポーネントが回転テンソルに表示されます。 三角法を簡素化する

 B_2:ishow(trigsimp(B_1))$ 

trigsim()関数は、三角関数式を単純化します。 この場合、ドキュメントに記述されているように、デフォルトでは、主な三角関数のアイデンティティと三角関数の偶数/奇数が考慮されます。 ただし、テンソル代数パッケージのロードがそのような効果があるかどうかにかかわらず、この関数は、上記のコックされたフラグがあっても、単一引数と半引数の関数を含む分数の単純化に出くわします。 それにもかかわらず、準備作業を実行し、出力で単純化された式を取得します



回転の半角の余弦と正弦の二乗を四元数のスカラーパラメータに置き換えるために残ります。このため、括弧の開示の形で置換と単純化を実行します。

 B_3:ishow(subst(p0,rhs(Lambda0), B_2))$ B_3:ishow(expand(subst(1-p0^2,sin(phi/2)^2, B_3)))$ 

結果を賞賛するために、LaTeXで出力します

 tentex(B_3); 

表示されたコードに左部分のみを追加しました



Maximaが生成するLaTeX表記は、自然な数学表記に非常に近いものであり、Mapleについては言えません。Mapleは、読みやすい式の導出で採用されたすべての規約を含む巨大なコードを準備します。 クロネッカーデルタを含む用語はグループ化されており、共通の要因は私たち自身によってまとめられています。 さて、「ラムダ」の場所に戻って



Rodrig-Hamiltonパラメーターに関して回転テンソルの式を取得しました。 このテンソルから、空間内の剛体の方向を記述する他のパラメーターに移動できます。

ウォームアップは終了したと見なすことができます。 もっと深刻な仕事が待っています

2. Rodrigue-Hamiltonのパラメーターにおける角速度の擬似ベクトル

Maximaに、角速度の疑似ベクトルについてすでに知っている式を導入します。 自然な形では、このように見えます



そして、Maximaでは、単一の角度の関数を半分の等価な関数で置き換えることになります

 Omega:ishow(2*sin(phi/2)^2*'levi_civita([],[i,m,r])*u([i],[])*diff(u([m],[]),t) + diff(u([],[r]),t)*2*sin(phi/2)*cos(phi/2) + u([],[r])*diff(phi, t))$ 

Levi-Civitaテンソルは、特にそのプロパティを使用して式を単純化する計画がある場合は、計算を抑制して導入することをお勧めします。 それ以外の場合、Maximaはそれを一般化されたクロネッカーデルタに変換しますが、これは計画に含まれていません。 計算を抑制するには、このテンソルを定義する関数の名前の前にアポストロフィを置きます。

角速度テンソルのインデックスの指定に従って、インデックスを省略し、回転単位ベクトルのインデックスの名前を変更します

 u_i:ishow(contract(Solv1[1]*g([i,j],[])))$ u_m:ishow(subst(m, i, u_i))$ ur:ishow(subst(r, j, Solv1[1]))$ 

置換で使用する式を取得します



単位ベクトルと回転角からの回転軸の導関数が必要です。 四元数のパラメータを介してそれらを表現する必要があります

 /*        */ du_mdt:ishow(diff(u_m, t))$ /*       */ dLambda0dt:diff(Lambda0, t); /*     */ Solv2:solve(dLambda0dt, diff(phi,t)); 

Maximaはすべての操作を正しく実行します



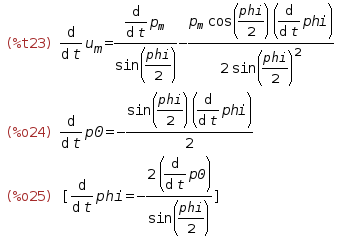
しかし、ここでもう1つ微妙な違いがあります。 結果の式から導関数を削除する必要があります。 それは完全に削除することです。 Maximaは式を単純化する一方で、それらに十分に応答しないためです。 たとえば、同じ導関数がサインの平方の係数と同じ角度の平方のコサインの係数として式にある場合、三角法を単純化するとき、Maximaは主要な三角関数のアイデンティティを強調として見ません。 そして、デリバティブが通常の表現で置き換えられると、アイデンティティは簡単に1つに崩れます。 同じことがテンソル変換にも当てはまります-操作に関与するテンソルの1つが他のテンソルの時間導関数によって表される場合、インデックスを省略し、Levi-Civitaテンソルで丸くなることは好ましくありません。 私はそれらを探していますが、問題の解決策を直接示すことはまだできていませんが、今のところ松葉杖の2番目を適用します-代替品を紹介します。 まず、角速度の式で、四元数のスカラーパラメーターの導関数を置き換えます

 dphidt:subst(v0, diff(p0,t), Solv2[1]); 

直接置換を実行しますsubst()関数の最初の引数は、2番目の引数によって裏切られた式を3番目の引数の式で置き換えるために必要なものです。 結果

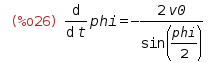
私たちに合っています。 次に、この角速度を、回転軸の単位ベクトルの秘密の導関数の式に代入します

 du_mdt:ishow(subst(dphidt, du_mdt))$ 

四元数の残りのパラメータの導関数を置き換えます

 du_mdt:ishow(subst(v([m],[]), diff(p([m],[]),t), du_mdt))$ 

インデックスを上げて、単位ベクトルの反変成分の導関数を取得します

 durdt:ishow(diff(u([],[r]),t) = contract(expand(rhs(du_mdt)*g([],[r,m]))))$ 

出力には、置換を実行するための式の完全なセットがあります



さて、それらを実行し、途中でブラケットを開き、Maximaに可能な限り小数部を削減させます

 Omega_1:ishow(subst(dphidt, Omega))$ Omega_1:ishow(expand(subst(du_mdt, Omega_1)))$ Omega_1:ishow(expand(subst(durdt, Omega_1)))$ Omega_1:ishow(expand(subst(u_i, Omega_1)))$ Omega_1:ishow(expand(subst(ur, Omega_1)))$ 

結果はすでにかなりまともです



しかし、第2項では、ゼロに等しいクォータニオン自体のベクトル部分のベクトル積が現れます。 SKAを削除するには、スペルを使用します

 Omega_2:ishow(canform(contract(expand(applyb1(Omega_1, lc_l, lc_u)))))$ 

このコマンドの作成の詳細は、 ここで説明します 。 私はポイントだけを思い出します-レビ-チビタテンソルの畳み込みを扱うためのルールに従ってテンソル表現を簡素化します。 呪文はゼロメンバーを削除します



ポイントが小さい-三角法をとかす

 Omega_3:ishow(trigsimp(Omega_2))$ 

残りの余弦をクォータニオンのスカラーパラメーターに置き換えます

 Omega_3:ishow(subst(lhs(Lambda0), rhs(Lambda0) , Omega_3))$ 

その結果、かなりコンパクトな式ができました



LaTeXに持ち込む

 tentex(Omega_3); 

天候はcanform()関数で番号付けされたダムインデックスによって損なわれますが、ここでは必要なインデックス名をすでに処理し、同時にcanform()ハミルトンパラメーターの導関数の場所に戻ります。



式（7）は、Rodrig-Hamiltonパラメーターに関する角速度の待望の式です。 ご覧のとおり、最終回転のパラメーターで記述された元の式よりもはるかにコンパクトです。 しかし、これが唯一のプラスの機能ではありません。 取得すると、別の便利な機能が開きます

3. Rodrigue Hamiltonのパラメーターの角加速度

角加速度を取得するには2つの方法があります。 最初のパス、最も単純なパスは、何らかの理由ですぐには到達しませんでしたが、時間を区別するだけです（7）。 これは簡単かつ迅速に手動で行われます。 正直にクロールした2番目の方法は、Maximaで式を取得し、最終的な回転のパラメーターを使用して既知の角加速度の表現を単純化することでした。



私は両方の方法をデモンストレーションします、私だけがスポイラーの下で長い道を歩むので、私の親愛なる読者が木の後ろの森を失いません。

したがって、（7）の時間微分をとります



最初の項はゼロであり、そのようなものはメンバーの相互破壊まであきらめられ、その結果、多くの困難なく、我々は得る





突然、（7）との完全な類似性が観察されますが、ここでの1次導関数の代わりに2次導関数があります。 導関数の係数は同じです。つまり、角速度と角加速度は、同じ行列（3 x 4）を乗算することにより、ロドリゲハミルトンパラメーターの対応する導関数から取得されます。 ちなみに、これにより、宇宙船の動きのモデリングや、空間で自由に回転する他のオブジェクトのモデリングにおけるクォータニオンアプローチの幅広い適用性が決まりました。

おわりに

この記事では、Maximaのテンソルライブラリを操作する方法に偏りがありました。 上記の仮定があっても、その中のテンソル式を単純化することは非常に便利であると結論付けることができます。

そして最後に、モデリングに便利なロドリゲ・ハミルトンの方向パラメーターを使用して、角速度と角加速度の式を取得しました。 そして、それらを表現する式（7）と（8）はコンパクトであるだけでなく、角速度と加速度ベクトルの成分に対する四元数へのパラメーターの同じ線形変換を使用するという意味で美しいことも確信しました。 このアプローチにより、モデル化プログラムの構成が大幅に簡素化されます。

今日まで、テンソル装置を使用して自由剛体のダイナミクスを検討することに近づきました。 次の記事を犠牲にして、私は興味深いアイデアを持っています。それを実装し、高品質の素材を準備しようとします。

ご清聴ありがとうございました！

継続するには...