一般的な情報
この記事では、算術式のパーサーをソフトウェアで実装するための可能なアルゴリズムの1つと、それらの値のその後の計算の可能性について検討します。
パーサーは、入力算術式を解析するプログラムです。 このクラスのプログラムは、「認識機能」とも呼ばれます。
解析は、入力算術式をより単純なコンポーネントに解析するプロセスです。
パーサーの結果は、形成されたトークンツリーです。 トークンとは、コンポーネント部分にさらに分解されない入力算術式のフラグメントを意味します。
認識アルゴリズムは、プログラミング言語に関係なく説明されています。 この記事は、PHPでのこのアルゴリズムの実装例で終わります。 このアルゴリズムは、ほとんどすべてのプログラミング言語で実装できます(OOPサポートがなくても)。
問題の声明
パーサーが入力で算術式を受け入れると仮定します。これは、
(x + 10.2)^ 2 + 5 * yzという形式の通常の行です。 入力式は算術式の文法に関して正しいです:
- 開き括弧の数は、閉じ括弧の数と同じです。
- 数値の整数部は、ドットで小数部から分離されます。
- 行には、有効な文字のみが含まれます:数字0 ... 9 、演算子+-* / ^ 、括弧、ピリオド、およびパラメーターx、y、z 。
パーサーは、入力式の数値の計算に適したトークンツリーを構築する必要があります。 パラメータ値を、数値の計算を実装するメソッドに渡します。
具体的な式ごとに、オブジェクトツリーが1回作成されます。 次に、結果のオブジェクトツリーを使用して、パラメーター値を考慮して出力式の最終値を計算します。 繰り返し計算は、無制限の回数にすることができます。
アルゴリズムは、括弧の入れ子のレベルを制限することなく、無制限の長さ(合理的な制限内)の入力式の処理を許可する必要があります。
入力式の字句解析
入力式の解析に直接進む前に、意味のない文字(スペースなど)を削除し、統合トークンを形成することをお勧めします。 この手順は、アルゴリズムのフレームワーク内では必須ではありませんが、アルゴリズムとそのソフトウェア実装の理解を大幅に簡素化できます。
例として、上記の算術式の行
(x + 10.2)^ 2 + 5 * yzの考察に戻ります。 字句解析のプロセスでは、指定された文字列は次の構造の文字列の配列に変換されます:
[0] =>”(”、[1] =>” x”、[2] =>” +”、[3] =>” 10.2”、 [4] =>”)”、[5] =>” ^”、[6] =>” 2”、[7] =>” +”、[8] =>” 5”、[9] => ” *”、[10] =>” y”、[11] =>”-”、[12] =>” z” 。
したがって、トークン全体は、演算子(算術演算)、オペランド(1つ以上の数字で構成される数値)、またはパラメーター(
x、y、z )またはブラケット(ストリング内の算術演算の優先順位を変更する要素として)のいずれかです。 )
オブジェクトとしてのトークン
ツリー構造の各統合トークンは、オブジェクトによって記述されます。 「ツリー」のオブジェクトには、一連のプロパティ(フィールド)と特定の動作があります。 トークンをモデル化する各オブジェクトのデータフィールドの提案されたセットをリストします。
- フィールド名 -オブジェクトの一意の名前を定義します。
- lecフィールドは、オブジェクトツリーの特定のノードを頂点とする入力式の部分に関する情報を格納するためのトークンの配列です。
- フィールドconst-このオブジェクトがパラメーターである場合、変数はその名前を格納します。
- フィールドvar-このオブジェクトが数値またはパラメーターの場合、変数はその値を格納します。
各オブジェクトの動作は、メソッドの組み合わせによって特徴付けられます。 この場合、1つのメソッドで十分です。たとえば、calc()です。 オブジェクトがオペランド(数値)またはパラメーターの動作を記述する場合、この数値またはパラメーター値を返す必要があります。 オブジェクトが演算子(算術演算)の1つであるトークンを記述する場合、メソッドはこの演算子を2つの数値に適用した結果を返す必要があります。
ツリー構造のすべてのオブジェクトは1つのクラスに属することができ、オブジェクトを作成するときに1つのメソッドを再定義するだけで十分です。 または、オプションとして、1つの抽象関数
calc()で抽象クラスを記述することができます。 次に、トークンのタイプごとに、抽象クラスを継承し、
calc()メソッドの特定の動作を定義するクラスを説明します。 ソフトウェア実装の例では、最後の方法が選択されたため、必要なコードの量が大幅に少なくなりました。
一部のフィールドは空白のままになる場合があります。特定のオブジェクトモデルがどのトークンに依存するかによって異なります。
ツリー構造のノードとしてのトークン
トークンをモデリングするオブジェクトの構成は、広く明確です。 しかし、ここで、これらのオブジェクトからツリー構造を形成する方法についての疑問が生じますか?
この問題は、ソフトウェアプロジェクトでは非常に一般的です。 ソリューションの本質は、「Linker」という名前のデザインテンプレートから取得できます。 このデザインパターン(パターン)のすべての複雑さのブラインドコピーは計画の一部ではないため、特定のケースで最も重要で必要なものを強調するよう努めています。
オブジェクトをツリー構造で構成するには、各オブジェクトにさらに3つのフィールドを追加します。
- childrenLeftフィールドは、このオブジェクトの左側の「子孫」です。
- childrenRightフィールドは、このオブジェクトの正しい「相続人」です。
- 親フィールドは、このオブジェクトの「親」です。
以下、「親」および「相続人」という用語は、OOPの重要な原則の1つを参照せずに、生成されたツリー構造で指定されたオブジェクトに対する他のオブジェクトの相対位置を示すコンテキストで使用されます。
上記を明確にするために、オブジェクトのすべてのフィールドの値を示す「(x + 10.2)^ 2 + 5 * yz」という式のツリー構造のイメージを提示します。
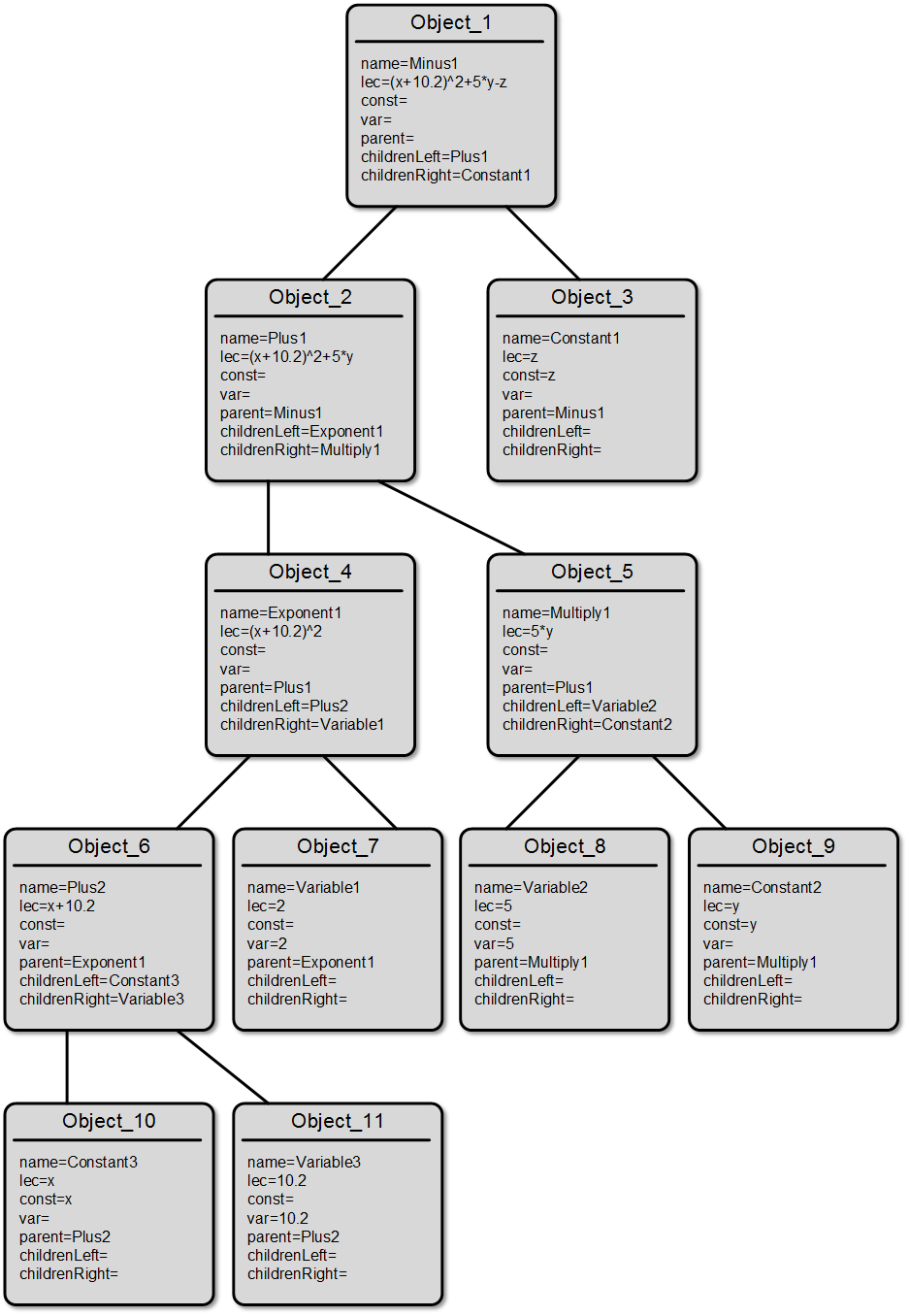
上記の図から、各ノードが「heirs」を2つしか持つことができない、またはまったく持つことができない理由が非常に明らかになります。
結果として生じるオブジェクトの構造は、ダイアグラムの一番上のオブジェクトの
calc()メソッドを呼び出すことにより、算術式の値を計算するのに非常に受け入れられます。
算術式の「変曲点」を検索する
算術式の「変曲点」とは、トークン配列の要素の1つを意味します。これは、演算子(算術演算)であり、他の演算子に対して最大の優先順位値を持ちます。
プログラムで算術演算の優先順位値を評価する機能を入力するには、次の構造を持つ配列を定義するだけで十分です。
[+] => 3、[-] => 3、[*] => 2、[/] => 2、[^] => 1 。
優先度の値が複数の演算子で最大の場合、最後の演算子を選択する必要があります。これにより、数値を正しく計算するツリー構造を作成できます。
次に、「変曲点」の左側の要素が
トークン配列で選択され、左側の「相続人」であるオブジェクトの
lecフィールドに書き込まれます。 「変曲点」の右側にある要素は、右側の「相続人」の同じフィールドに入力されます。 また、変曲点を検索するときは、ソリッドトークンの配列内のブラケットの入れ子のレベルを考慮する必要があることにも注意してください。
ツリー構造の構築
このセクションでは、提案されたアルゴリズムのフレームワーク内でのオブジェクトの「ツリー」の形成シーケンスを詳細に分析します。
ルートオブジェクトとその2つの「heirs」を含む、「ツリー」の最初の3つのオブジェクトを構築する手順を検討します。 入力で算術式全体のトークン全体の配列を受け取ると、その中に「変曲点」が見つかります。 これは常に演算子(算術演算)であることを思い出させてください。 見つかった「変曲点」の値により、構造の最上部にあるオブジェクトのクラスを一意に決定できます。 次に、前述のように、トークンの配列を2つの部分に分割します。 両方の部分のそれぞれに、「変曲点」もあります。これは、左右の「相続人」のオブジェクトのクラスを示しています。 これで、3つのオブジェクトすべてを形成し、それらの間の関係を示すことができます。
最後に、オブジェクトはその後のアクションのために
arNode配列に配置されます。
入力式:
(x + 10.2)^ 2 + 5 * yzの場合、説明されている手順は次のとおりです。 2つの演算子は、変曲点の定義に該当します:「+」(数字「2」と「5」の間)および「-」。 リストの最後の演算子「-」を選択します。 この演算子の値により、ルートオブジェクトの必要なクラスとその名前を選択できます。 特に、
Minusクラスのオブジェクトは
Minus1という名前で形成されます。 トークンの初期配列を2つの部分に分割した後、2つの要素配列
(x + 10.2)^ 2 + 5 * yおよび
zを取得します。 最初のトークンでは、変曲点は「+」で、2番目は1つの要素
zのみで構成されます。 これは、ルートオブジェクトの「相続人」として、
Plus1および
Constant1という名前の
Plusおよび
Constantクラスのオブジェクトをそれぞれ作成する必要があることを意味します。 新たに作成されたオブジェクト
childrenLeft 、
childrenRightおよび
parentのフィールドに入力して、ツリー構造を形成し、オブジェクトを
arNode配列に追加します。
「ツリー」のさらなる形成は、最初の3つを作成する手順と非常に似ていますが、独自の微妙な点があります。
arNode配列で
は 、配列の要素
を単純に検索し、配列内に複数の要素を含む
lecフィールドを持つオブジェクトを探し、同時に空の
childrenLeftフィールドと
childrenRightフィールドを探します。 選択したオブジェクトから
lecフィールドの値を読み取り、「変曲点」で2つの部分に分割します。 次に、結果の両方の部分の「変曲点」を見つけ、上記のロジックに従って、選択したオブジェクトの2つの継承オブジェクトを形成します。 オブジェクト間の関係を形成し、オブジェクト自体を
arNode配列に追加することを忘れないでください。
示された条件に対応するツリー構造のオブジェクトがなくなるまで、示されたアクションのシーケンスを繰り返します。 これで、入力式の「ツリー」が構築され、値を計算する準備ができたと仮定できます。
値の計算
アルゴリズムのソフトウェア実装のリストを表示すると、入力算術式の値を計算するプロセスが非常に明確になります。 いくつかの重要な点について説明します。
計算は、クラス
Mainのオブジェクトの
calc()メソッドを呼び出した後に行われます。 プログラムは、このメソッドを呼び出すときに
x 、
y 、
zの 3つ以下のパラメーターを使用する機能を提供します。 説明したアルゴリズムの特定のアプリケーションのニーズを考慮して、この量を変更するのは簡単です。
最初に、メソッドはパラメータートークンを記述するオブジェクトの配列を検索し、次に
calc()メソッド呼び出しで指定された数値が、見つかったオブジェクトの
varフィールドに入力されます。 これで、
arNode配列
で空の
親フィールド(これはツリー構造のルートオブジェクトになります)
を持つオブジェクトの検索を開始し、その
calc()メソッドを呼び出すことができます。 このメソッドは、算術式の値を返します。
ソフトウェア実装例
ソフトウェア実装全体のリストをレイアウトすることが決定されました。 これにより、試してみたり、改良したりする必要がある場合に、プログラム全体をコピーできます。
<!DOCTYPE html> <html> <head> <meta charset="UTF-8"> <title></title> </head> <body> <?php class Main {
プログラムの最後で3つの連続した
エコー演算子からコメントを削除すると、ツリー構造の形成の正確性を分析し、すべてのオブジェクトのフィールドの値を確認できます。
おわりに
できるだけ詳細にアルゴリズムを説明しようとしましたが、質問がある場合は、書いてください。みんなに答えようとします。 また、本文に記載されている誤りや不正確さの報告をいただければ幸いです。