連続分散ランダムジェネレーター

乱数ジェネレーターはセックスによく似ています。良いときは美しく、悪いときはまだいいです（George Marsaglia、1984）

確率的アルゴリズムの人気は高まっています。 それらの多くは、多数の異なるランダム変数の生成に基づいています。 常に均一に分布しているとは程遠い。 ここでは、既知の分布を持つ高速で正確なランダム値ジェネレーターに関する情報を収集しようとしました。 タスクは異なる場合があり、基準は異なる場合があります。 ある人にとっては、生成時間は重要です。他の人にとっては-精度、他の人にとって-暗号の安定性、他の人にとって-収束の速度です。 個人的には、0から特定のRAND_MAXまで均一に分布した擬似乱数整数を返す特定の基本的なジェネレーターがあるという前提から進めました。

unsigned long long BasicRandGenerator() { unsigned long long randomVariable; // some magic here ... return randomVariable; } 

そして、このジェネレーターは十分に高速です。 つまり、対数を計算したり、それらの1つを累乗したりするよりも、数十個の乱数を生成する方が安価です。 これらは標準のジェネレーターです：std :: rand（）、MATLABのrand、Java.util.Randomなど。 ただし、このようなジェネレーターは深刻な作業に適していることはほとんどありません。 多くの場合、異なる統計テストに失敗します。 また、それらに完全に依存していることを忘れないでください。独自のジェネレーターを使用して、その動作を把握することをお勧めします。

この記事では、アルゴリズムについて説明します。アルゴリズムの本質は、少なくとも確率理論に出くわすことがある人には明らかなはずです。 計測の理論に精通する必要はありません。原則として、分布関数と分布密度関数がどのようなものかを大まかに理解すれば十分です。


各アルゴリズムには、コード、少量の数学、および生成された数千万のランダム変数のヒストグラムを添付します。

均一な分布

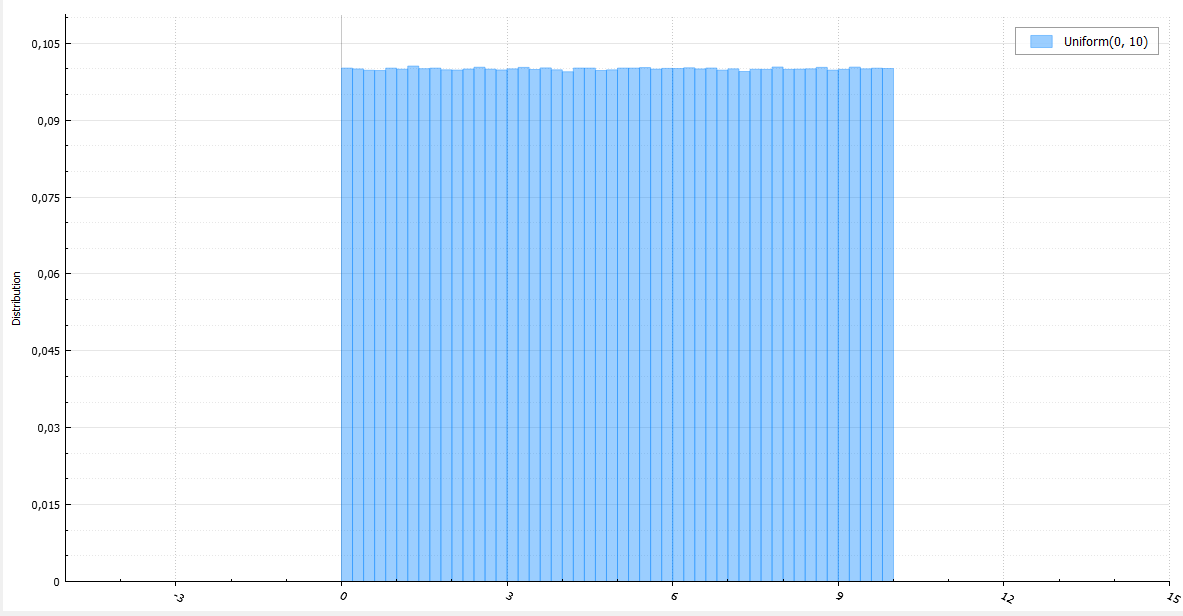
非常にシンプルで普遍的な逆変換サンプリング方法があるため、均一分布を使用してほぼすべてのランダム変数を生成できます.0から1に均一に分布するランダム変数Uを生成し、パラメーターUで逆分布関数（分位点）を返します。確かに：


問題は、分析的に可能な限り、逆分布関数のカウントが長くなる可能性があることです。

一様分布ジェネレーターを使用すると、長時間停止する必要はありません（多数のランダム変数が生成されるため、（b-a）/ RAND_MAXを1回だけカウントすることをお勧めします）。

 double Uniform(double a, double b) { return a + BasicRandGenerator() * (b - a) / RAND_MAX; } 

もちろん、継続性は単なる抽象化です。 現実の世界では、この場合、具体的にはこれはかなり小さなサンプリングステップを意味します。 重要なことは注目に値します。 0から1に均等に分布する乱数を生成する場合、32ビットでは、doubleがこの範囲で取ることができるすべての値をカバーするには不十分です（ただし、floatには十分です）。 品質を向上させるには、64ビット整数を生成するか、2つの32ビット整数を結合する必要があります。

正規分布

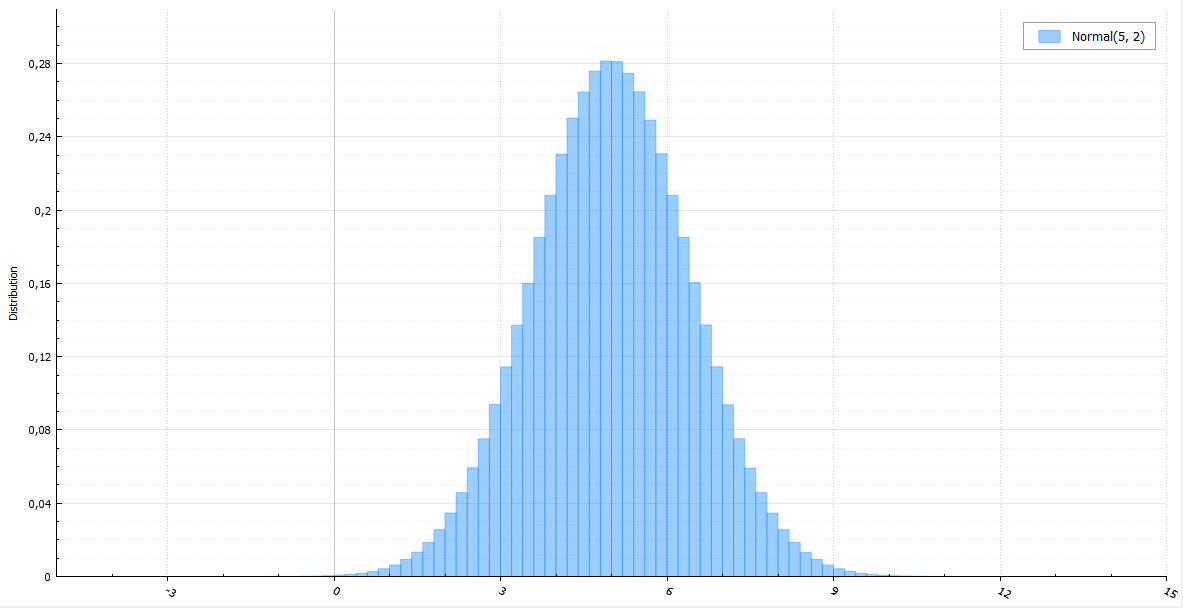
反転法では、逆誤差関数の計算が必要になります。 特別な近似関数を使用しない場合、それは難しく、信じられないほど長くなります。 通常の値の場合、Box-Mullerメソッドが存在します。 それは非常にシンプルで普及しています。 その明らかな欠点は、超越関数の計算です。 Habréでは、 ポーラー法がすでに言及されており、サインとコサインの計算を避けるのに役立ちました。 ただし、対数とその根を数える必要があります。 同じ極法の作者であるジョージ・マルサグリアによって発明された美しい名前のジグラット法は、はるかに高速です。
極座標法は、 受入拒否サンプリングの例です。 文字通り、値を生成し、適合する場合はそれを受け入れます。それ以外の場合は、拒否して再度生成します。 主な例：密度f（x）のランダム変数を生成する必要がありますが、単純な反転法で行うのは非常に困難です。 しかし、f（x）とそれほど変わらない密度g（x）のランダム変数を生成できます。 この場合、M> 1およびほぼすべての場所でf（x）<Mg（x）となる最小の定数Mを取得し、次のアルゴリズムを実行します。

• 分布g（x）からランダム変数Xを生成し、0から1まで一様に分布したランダム変数Uを生成します。
• U <f（X）/ Mg（X）の場合-Xを返し、そうでない場合-繰り返します。

ランダム変数を取る確率：


Mの選択が少ないほど、この確率は高くなりますが、ジェネレーターの動作は速くなります。



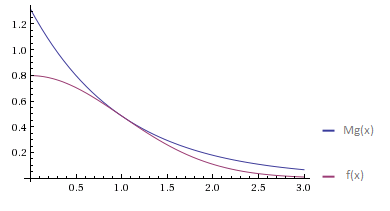
たとえば、標準の標準値のモジュールを生成します。 正規分布の対称性により、得られた値は、等しい確率で値+1および-1をとるランダム変数で乗算され、標準正規分布値Xを取得できます。正規値は、シグマによる標準乗算とmuによるシフトから取得されます。 分布密度関数| X |：


標準の指数分布の密度関数で近似してみましょう。 指数分布についてはまだ話していないので、少し先に進んでいます。 単純に悪名高い反転法によって生成されます-[0、1]に均一に分布した量Uを取り、-ln（U）を返します。


条件f（x）<Mg（x）を満たすMの最小値は、x = 1で達成されます。


次に：


また、通常のランダム変数を生成するためのアルゴリズムは次のとおりです。

1. U-[0、1]に均一に分布するランダム変数を生成します。
2. 指数関数的に分布するランダム変数Eを生成します（-ln（U）をカウントするよりも高速なアルゴリズムについて、以下で説明します）。
3. U <exp（-（E-1） ² ）の場合| X | = E、それ以外の場合は最初のステップに戻ります。
4. 新しいUを生成します。U<0.5の場合、-| X |または| X |を返します。 別の場合。

それは簡単にわかります：


そしてこれは、Uの代わりに、指数関数的に考慮されない別の指数分布量を生成できることを意味します。 新しいアルゴリズムは次のようになります。

1. 標準の指数分布ランダム変数E ₁およびE ₂を生成します。
2. E ₂ >（E 1-1）2/2の場合、| X | = E ₁ 、それ以外の場合は戻ります。
3. Uを生成します。U<0.5の場合、-| X |または| X |を返します。 別の場合。

別のポイント：値E _1が受け入れられると、差E _2- （E 1-1）2/2も指数関数的にかつE ₁とは独立して分布します。 したがって、次回はE _1の代わりに記憶して使用できます。


偏差のあるサンプリングの一般的な問題は、偏差が可能な限り小さくなるように分布密度g（x）のランダム変数を選択することです。 この問題を解決する多くの拡張機能があります。 メソッド自体は、Zigguratを含むほとんどすべての後続アルゴリズムの基礎です。 後者の本質は依然として同じです。正規分布の密度関数を同様の単純な関数でカバーし、曲線の下にある値を返すようにします。 この関数は独特であり、多段構成に似ていますが、実際はアルゴリズムの名前です。


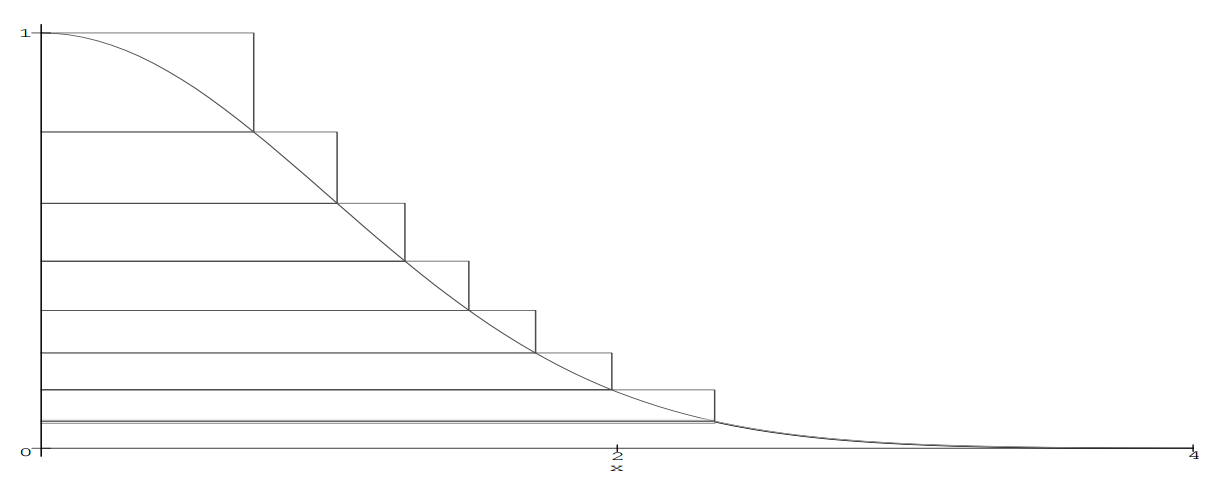
ジグラットは次のように構成されています。 関数f（x）のふもとで、点x ₁およびy ₀ = f（x ₁ ）が選択されます。 長方形の下の領域は（0,0）から（x ₁ 、y ₀ ）+関数fの尾の下の領域（x> x ₁ ）= Aです。したがって、ベースレイヤーを構築しました。 その上部には別の長方形があり、その幅はx ₁ 、高さはy ₁ = A / y _0であり、したがって面積はAと等しくなります。この長方形には、関数f（x）の上にある点が既に含まれています。例：（x ₁ 、y ₁ ）。 2番目の長方形は、ポイント（x ₂ 、y ₁ ）で関数f（x）と交差します-これは、3番目の長方形の右下点の座標になります。関数の最上部にZigguratを構築しません。 各ステップの面積はAに等しくなります。さらなるアルゴリズム（ベースレイヤーに入る処理なし） ：

1. 長方形iがランダムかつ均等に選択され、均一に分布した値Xが0からx _iまで生成されます
2. X <x _{i + 1の}場合、間違いなく曲線の下に落ちます-Xを返します。
3. y _iからy _{i + 1}までのYの新しい一様分布値を生成します。 座標（X、Y）を持つポイントが曲線の下にある場合、つまりY <f（X）の場合、Xを返します。それ以外の場合、最初のステップに戻ります。

ベースレイヤーにいる場合はどうしますか？ 想像上の点x ₀ = A / y _0を入力することにより、そこから面積Aの長方形を作成することもでき_ます 。 次に、（0,0）から（x ₀ 、y ₀ ）までの長方形の面積もAに等しくなります。ベースレイヤーの違いは、新しい想像上の長方形の曲線に該当しない場合、xを拒否してはならないことです。ただ尾を打ちます。 尾については、ジョージ・マルサグリアは、以前に検討したのと同じ方法を使用することを提案します-偏差のあるサンプリング。 いくつかの変更のみ：

1. 密度x _1の標準的な指数分布ランダム変数E ₁と単位密度のE ₂を生成します。
2. E ₂ > E ₁ 2/2の場合、| X | = E ₁ + x ₁ 、それ以外の場合は戻ります。
3. Uを生成します。U<0.5の場合、-| X |または| X |を返します。 別の場合。

すると、アルゴリズム全体は次のようになります。

1. 長方形iはランダムかつ均等に選択され、0からx _iまでの一様分布値Xが生成されます。
2. X <x _{i + 1の}場合、間違いなく曲線の下に落ちます-Xを返します。
3. ベースレイヤー、つまりi = 0にヒットした場合、テールに対してアルゴリズムを実行し、その結果を返します。
4. y _Iからy _{i + 1}までYの新しい一様分布値を生成します。 座標（X、Y）を持つポイントが曲線の下にある場合、つまりY <f（X）の場合、Xを返します。それ以外の場合、最初のステップに戻ります。

問題は、長方形の数に応じて定数Aとx ₁を見つける方法ですか？ それらは通常の数値的方法で見つけることができます。 最初の仮定x ₁を取得し、ベースレイヤーを構築し、Aを計算して、必要な数の四角形を構築するまでジグラットを構築します。 関数よりも高い場合-つまり、x _1の値が小さすぎて、Aの値が大きすぎる場合-新しい値で再構築しようとしています。

アルゴリズム自体は、32ビット整数を使用して不要な乗算を削除するさまざまなトリックによって高速化できます。 詳細については、George MarsagliaおよびWai Wan TsangのThe Ziggurat Method for Generation Random Variablesを参照してください。 ここでは、完全に最適化されているわけではありませんが、理解可能なコードを示します（指数分布を生成できる場合）。

 static double stairWidth[257], stairHeight[256]; const double x1 = 3.6541528853610088; const double A = 4.92867323399e-3; /// area under rectangle void setupNormalTables() { // coordinates of the implicit rectangle in base layer stairHeight[0] = exp(-.5 * x1 * x1); stairWidth[0] = A / stairHeight[0]; // implicit value for the top layer stairWidth[256] = 0; for (unsigned i = 1; i <= 255; ++i) { // such x_i that f(x_i) = y_{i-1} stairWidth[i] = sqrt(-2 * log(stairHeight[i - 1])); stairHeight[i] = stairHeight[i - 1] + A / stairWidth[i]; } } double NormalZiggurat() { int iter = 0; do { unsigned long long B = BasicRandGenerator(); int stairId = B & 255; double x = Uniform(0, stairWidth[stairId]); // get horizontal coordinate if (x < stairWidth[stairId + 1]) return ((signed)B > 0) ? x : -x; if (stairId == 0) // handle the base layer { static double z = -1; double y; if (z > 0) // we don't have to generate another exponential variable as we already have one { x = Exponential(x1); z -= 0.5 * x * x; } if (z <= 0) // if previous generation wasn't successful { do { x = Exponential(x1); y = Exponential(1); z = y - 0.5 * x * x; // we storage this value as after acceptance it becomes exponentially distributed } while (z <= 0); } x += x1; return ((signed)B > 0) ? x : -x; } // handle the wedges of other stairs if (Uniform(stairHeight[stairId - 1], stairHeight[stairId]) < exp(-.5 * x * x)) return ((signed)B > 0) ? x : -x; } while (++iter <= 1e9); /// one billion should be enough return NAN; /// fail due to some error } double Normal(double mu, double sigma) { return mu + NormalZiggurat() * sigma; } 

指数分布

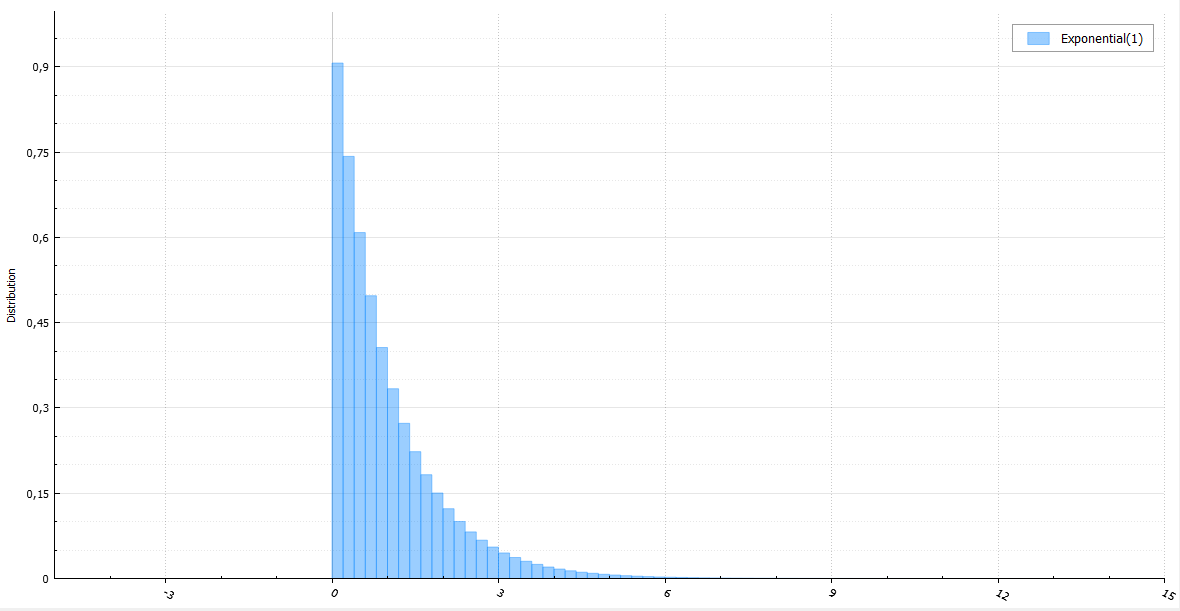
指数分布の場合、均一に分布した量の対数をとることができ、生成を高速化できるとすでに言われています。 任意の指数値は密度による標準的な除算から取得されるため、生成は悪名高いジグラットにすることができます。 末尾に到達した場合、アルゴリズムを新しい方法で実行し、取得した値にx ₁を追加できます。


さらに2つの事実：255個の長方形のテーブルを使用する場合、指数分布の最初の受け入れ確率は0.989で、通常の分布では0.993です。 MATLABでは、バージョン5以降、正規分布にZigguratが使用されています（極法が使用されていました）。 Rでは、通常の量については、私の知る限り、逆誤差関数を多項式で近似し、反転法を使用します。

 static double stairWidth[257], stairHeight[256]; const double x1 = 7.69711747013104972; const double A = 3.9496598225815571993e-3; /// area under rectangle void setupExpTables() { // coordinates of the implicit rectangle in base layer stairHeight[0] = exp(-x1); stairWidth[0] = A / stairHeight[0]; // implicit value for the top layer stairWidth[256] = 0; for (unsigned i = 1; i <= 255; ++i) { // such x_i that f(x_i) = y_{i-1} stairWidth[i] = -log(stairHeight[i - 1]); stairHeight[i] = stairHeight[i - 1] + A / stairWidth[i]; } } double ExpZiggurat() { int iter = 0; do { int stairId = BasicRandGenerator() & 255; double x = Uniform(0, stairWidth[stairId]); // get horizontal coordinate if (x < stairWidth[stairId + 1]) /// if we are under the upper stair - accept return x; if (stairId == 0) // if we catch the tail return x1 + ExpZiggurat(); if (Uniform(stairHeight[stairId - 1], stairHeight[stairId]) < exp(-x)) // if we are under the curve - accept return x; // rejection - go back } while (++iter <= 1e9); // one billion should be enough to be sure there is a bug return NAN; // fail due to some error } double Exponential(double rate) { return ExpZiggurat() / rate; } 

ガンマ分布

生成のためのアルゴリズムはここではすでに複雑であるため、ここではそれらの証拠を説明しません。例のみを示します。 標準値（シータ= 1）を生成するには、それぞれkに依存する4つのアルゴリズムが使用されます。

• kまたは2kが整数で、k <5がGAアルゴリズムの場合。
• k <1の場合-GSアルゴリズム。
• 1 <k <3の場合-GFアルゴリズム。
• k> 3の場合-GOアルゴリズム。

非標準のガンマ確率変数は、シータによる標準の乗算から取得されます。

GAアルゴリズム

パラメーターk1とk2のガンマ分布を持つ2つのランダム変数を追加すると、パラメーターk1 + k2のガンマ分布を持つランダム変数が得られます。 別の特性として、シータ= k = 1の場合、分布が指数関数的であることを簡単に検証できます。 したがって、kが整数の場合、単純に標準の指数分布でk個のランダム変数を加算できます。

 double GA1(int k) { double x = 0; for (int i = 0; i < k; ++i) x += Exponential(1); return x; } 

kが整数ではなく、2kが整数の場合、合計で指数ランダム変数の1つではなく、通常値の2乗の半分を使用できます。 なぜこれが可能かは、後で明らかになります。

 double GA2(double k) { double x = Normal(0, 1); x *= 0.5 * x; for (int i = 1; i < k; ++i) x += Exponential(1); return x; } 

GSアルゴリズム

1. 0から1 + k / eまで一様に分布するEの標準的な指数分布値とUの値を生成します。 U <= 1の場合、手順2に進みます。それ以外の場合、手順3に進みます。
2. x = U ^{1 / k}を設定します。 x <= Eの場合はxを返し、そうでない場合は手順1に戻ります。
3. x = -ln（（1-U）/ k + 1 / e）を設定します。 （1-k）* ln（x）<= Eの場合、xを返します。それ以外の場合、手順1に戻ります。

 double GS(double k) { // Assume that k < 1 double x = 0; int iter = 0; do { // M_E is base of natural logarithm double U = Uniform(0, 1 + k / M_E) double W = Exponential(1) if (U <= 1) { x = pow(U, 1.0 / k); if (x <= W) return x; } else { x = -log((1 - U) / k + 1.0 / M_E); if ((1 - k) * log(x) <= W) return x; } } while (++iter < 1e9); // excessive maximum number of rejections return NAN; // shouldn't end up here } 

GFアルゴリズム

私の知る限り、このアルゴリズムの著者であるノースカロライナ大学のJ. S.フィッシュマン教授は、彼の業績を発表していません。 アルゴリズム自体はk> 1で機能しますが、その平均実行時間はsqrt（k）に比例して増加するため、k <3に対してのみ有効です。

1. 標準的な指数分布を持つ2つの独立したランダム変数E ₁およびE ₂を生成します。
2. E ₂ <（k-1）*（E ₁ -ln（E ₁ ）-1）の場合、手順1に戻ります。
3. x = k * E _1を返します

 double GF(double k) { // Assume that 1 < k < 3 double E1, E2; do { E1 = Exponential(1); E2 = Exponential(1); } while (E2 < (k - 1) * (E1 - log(E1) - 1)); return k * E1; } 

GOアルゴリズム

Dieter and Ahrensアルゴリズムは、パラメーターの増加に伴う分布の漸近正規性に基づいているため、kが大きいほど高速です。 k> 2.533で機能しますが、k <3のフィッシャーアルゴリズムほど効果的ではありません最初に、いくつかの定数を設定する必要があります（kのみに依存）。

 void setupConstants(double k) { m = k - 1; s_2 = sqrt(8.0 * k / 3) + k; s = sqrt(s_2); d = M_SQRT2 * M_SQRT3 * s_2; b = d + m; w = s_2 / (m - 1); v = (s_2 + s_2) / (m * sqrt(k)); c = b + log(s * d / b) - m - m - 3.7203285; } double GO(double k) { // Assume that k > 3 double x = 0; int iter = 0; do { double U = Uniform(0, 1); if (U <= 0.0095722652) { double E1 = Exponential(1); double E2 = Exponential(1); x = b * (1 + E1 / d); if (m * (x / b - log(x / m)) + c <= E2) return x; } else { double N; do { N = Normal(0, 1); x = s * N + m; // ~ Normal(m, s) } while (x < 0 || x > b); U = Uniform(0, 1); double S = 0.5 * N * N; if (N > 0) { if (U < 1 - w * S) return x; } else if (U < 1 + S * (v * N - w)) return x; if (log(U) < m * log(x / m) + m - x + S) return x; } } while (++iter < 1e9); return NAN; // shouldn't end up here; } 

以前の分布の場合と同様に、ガンマ値はシータパラメータによる標準の乗算から生成されます。 一様分布、正規分布、指数分布、ガンマ分布を生成できれば、他の分布のほとんどを簡単に取得できます。これらは上記で簡単に表現できるためです。

コーシー分布

コーシー分布で確率変数をすばやく取得する1つの方法は、2つの正規確率変数を取得し、それらを互いに分割することです。 もっと速くできますか？通常の反転方法を使用できますが、接線の計算が必要になります。これはさらに遅いです。

かどうか？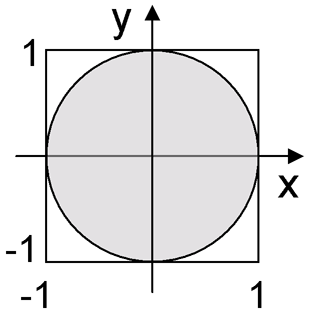

ジョージ・マルサグリアの極法を覚えていますか？彼は、Box-Muller変換で、均一に分布したランダム変数のサインまたはコサインをすばやく取得することを許可しました。接線を取得する方法とまったく同じです。正方形[-1、1] x [-1、1]に2つの均等に分布したランダム座標xおよびyを生成します。（0、0）を中心とする円と単位半径に到達した場合-x / yを返します。それ以外の場合-xとyを再度生成します。たとえば、3回目はすでに0.01未満であるため、円に陥らない確率。

 double Cauchy(double x0, double gamma) { double x, y; do { x = Uniform(-1,1); y = Uniform(-1,1); } while (x * x + y * y > 1.0 || y == 0.0); return x0 + gamma * x / y; } 

ラプラス分布

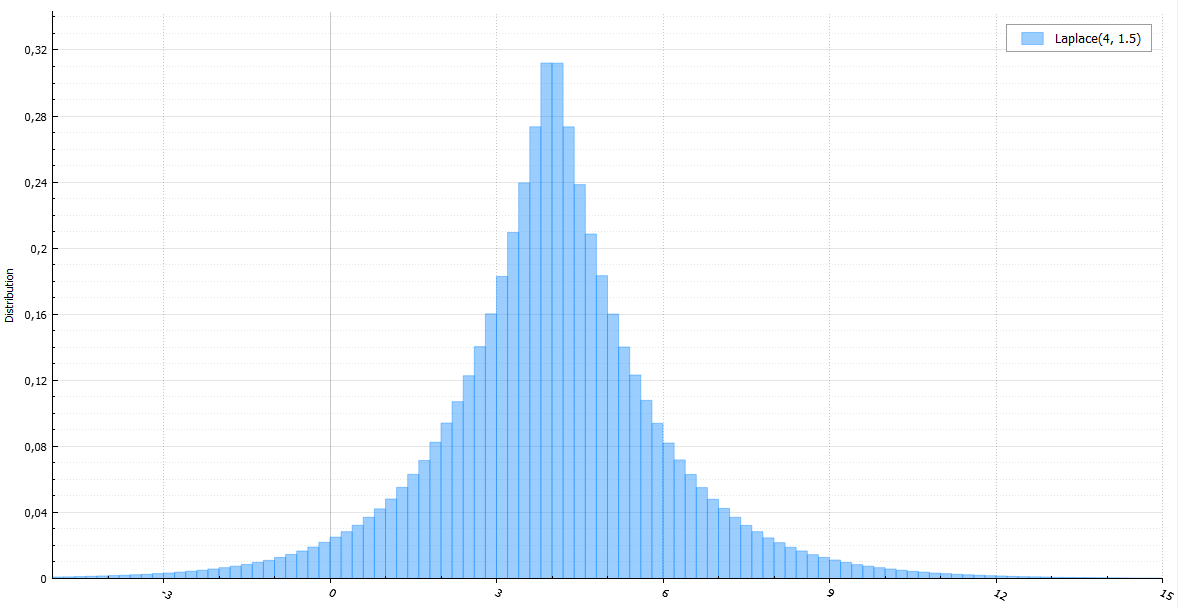ラプラス分布は同じ指数ですが、ランダムな符号を持ちます。

 double Laplace(double mu, double b) { double E = Exponential(1.0 / b); return mu + (((signed)BasicRandGenerator() > 0) ? E : -E); } 

課税分配

分布密度関数がどれほどひどいものであっても、ランダム変数自体は非常に簡単かつ迅速に生成されます。

 double Levy(double mu, double c) { double N = Normal(0, 1); return mu + c / (N * N); } 

カイ二乗分布

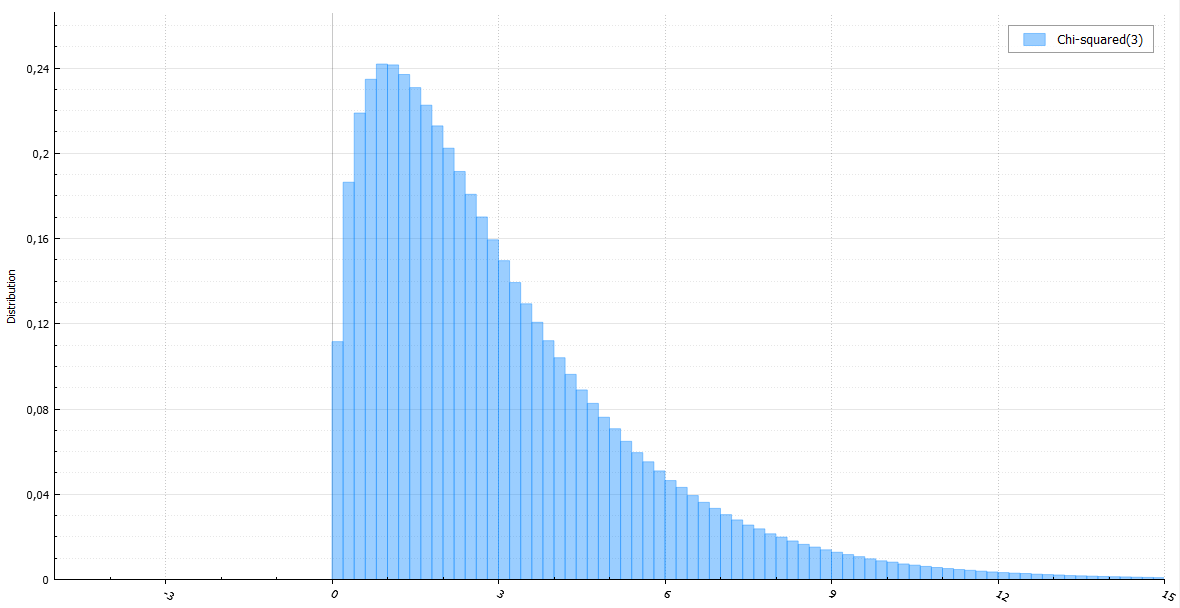ご存知のように、パラメータkのカイ2乗分布を持つ確率変数は、k個の標準正規確率変数の平方和です。kでさえ、これがk / 2指数確率変数（またはアーラン分布）の2倍和であることはあまり知られていません。この関係から、前述のGA2アルゴリズムは以下を導き出します。

 double ChiSquared(int k) { // ~ Gamma(k / 2, 2) if (k >= 10) // too big parameter return GO(0.5 * k); double x = ((k & 1) ? GA2(0.5 * k) : GA1(k >> 1)); return x + x; } 

このプロパティから注目すべき事実があります。平面上の点をランダム座標と法線座標（x、y）で選択すると、（0,0）からこの点までの距離は指数関数的に分布します。

対数正規分布

金融市場で数学モデルを扱う人は、対数正規分布を直接知っています。対数正規分布、対数コーチ分布、対数ロジスティック分布の場合、簡単な方法が1つあります。指数を取ることです。残念ながら、より高速な方法はわかりませんが、レヴィ分布やカイ二乗分布を使用して同様の量を生成する方法があるかもしれません。それらがどれほど似ているかを見てください。それまでの間、このように：

 double LogNormal(double mu, double sigma) { return exp(Normal(mu, sigma)); } 

ロジスティック分布

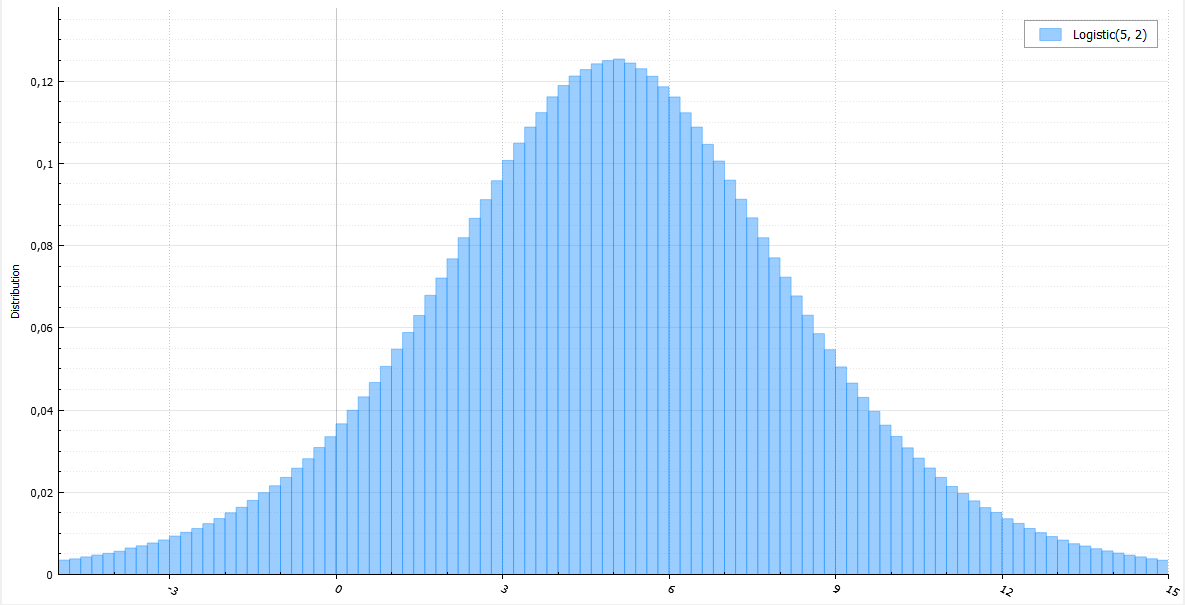ロジスティック分布は正規分布と非常に似ていますが、テールが大きく、標準の均一分布を介して非常に簡単に生成されます。

 double Logistic(double mu, double s) { return mu + s * log(1.0 / Uniform(0, 1) - 1); } 

最後に、常に高速というわけではありませんが、他の一般的なディストリビューション用の非常に単純なアルゴリズムについて簡単に説明します。

 double Erlang(int k, double l) { return GA1(k) / l; } double Weibull(double l, double k) { return l * pow(Exponential(1), 1.0 / k); } double Rayleigh(double sigma) { return sigma * sqrt(Exponential(0.5)); } double Pareto(double xm, double alpha) { return xm / pow(Uniform(0, 1), 1.0 / alpha); } double StudentT(int v) { if (v == 1) return Cauchy(0, 1); return Normal(0, 1) / sqrt(ChiSquared(v) / v); } double FisherSnedecor(int d1, int d2) { double numerator = d2 * ChiSquared(d1); double denominator = d1 * ChiSquared(d2); return numerator / denominator; } double Beta(double a, double b) { double x = Gamma(a); return x / (x + Gamma(b)); } 

C ++ 17でこれらおよび他のジェネレーターを実装する