むかしむかし、私はハブ
に関する記事に出くわしました。そこでは、人々はすべてがいかにクールで、ミンコフスキーメトリックがどれほどうまく機能するかを書いています。 時間は過ぎ去りましたが、私はすべてを望み、望みました。 最後に、私はこの奇跡を適用したいと思ったタスクを見つけました。

いや、いや、いや、今私がやるなら、あなたはその記事さえ読まないでしょう。 なります。 しかし、後で。 そしてその前に、それがすべて始まったタスクを説明したい:
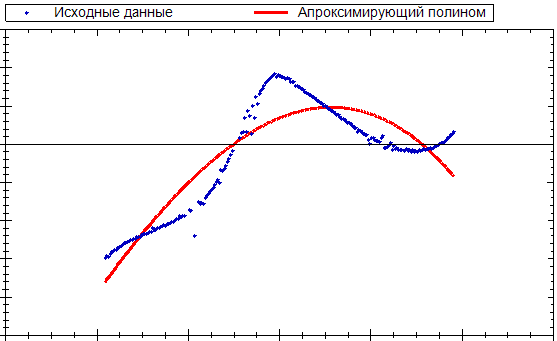

アルゴリズムのすぐ前は、かなり高品質の近似値です。 それを責めるものは何もありません:結果の多項式への収束は非常に遅く、標準偏差は変更に消極的です。また、開始点の数が少ないため(約200個)、残差の分布は通常のように最初の近似に見えます。
そして、普遍的な基準を求めて。 これにより、ランダムシーケンスと通常のシーケンスを区別できるようになります(これが問題全体であることはわかっていますが、それでもなお)、アイデアはフラクタルを使用して思いつきました。 実際、ランダムウォークの次元は1.5です。 残差曲線の次元を計算することにより、1.5 +-妥当な値が得られることが望まれます。
Hausdorff次元の計算はまだ仕事ですが、Minkowskiではすべてが非常に簡単になりました。
最初の記事で使用されているアプローチを適用します。スケールを変更し、曲線が通過する長方形の数Nを考慮します。 依存関係ログ(N(e))/ log(e)を取得したら、最小二乗法を使用して直接近似します。 私たちが探している測定基準は勾配係数です。
public double calculate(IEnumerable<KeyValuePair<double, double>> dataList) { double minY = Double.MaxValue, maxY = Double.MinValue; double minX = minY, maxX = maxY; foreach (var pair in dataList) { if (minY > pair.Value) minY = pair.Value; if (maxY < pair.Value) maxY = pair.Value; if (minX > pair.Key) minX = pair.Key; if (maxX < pair.Key) maxX = pair.Key; } m_bottomLeftY = minY; m_bottomLeftX = minX; return calculate(dataList, maxX, maxY); } public double calculate(IEnumerable<KeyValuePair<double, double>> dataList, double maxX, double maxY) { if( dataList.Count() < 2) return 0; for(int scaleNumber = StartSize; scaleNumber !=FinishSize; ++scaleNumber){ double XScale = (maxX - m_bottomLeftX) / scaleNumber; double YScale = (maxY - m_bottomLeftY) / scaleNumber; var enumerator = dataList.GetEnumerator(); fillBoxes( (ref double x, ref double y) => { var res = enumerator.MoveNext(); if (res) { x = enumerator.Current.Key; y = enumerator.Current.Value; } return res; }, XScale, YScale); int count = calculatedNumberBoxesAndReset(scaleNumber); if (count == 0) count = 1; m_boxesNumber[scaleNumber - StartSize] = Math.Log(count); } m_linearApproximator.approximate(m_scaleArgument, m_boxesNumber); return m_linearApproximator.resultPolinomal.a[1]; } double m_bottomLeftX, m_bottomLeftY;
元の記事とは異なり、スケールを変更するのは等比数列ではなく、算術では、最初のデータが少なすぎます。
m_linearApproximatorはOLSのラッパーであり、スマートで複雑なものではありませんが、OLSは元の記事でも見つけることができます。 MathNet.Numericsのいずれか。
if(count == 0)count = 1という行は、実装の詳細のために発生しました。 1つのポイントしかない場合をカバーします。
すべての魔法はfillBoxesメソッドにあり、これは正方形が塗りつぶされる場所です。
void fillBoxes(GetDataDelegate dataIterator, double stepX, double stepY) { double prevX=0, prevY=0, targetX=0, targetY=0; dataIterator(ref prevX, ref prevY); int indexY = FinishSize, indexX = FinishSize; int currentIndexX= calculateIndex(m_bottomLeftX, stepX, prevX), currentIndexY =calculateIndex(m_bottomLeftY, stepY, prevY) ; m_Boxes[currentIndexY, currentIndexX] = true; double[] CrossPosition = new double[2]; while (dataIterator(ref targetX, ref targetY)) { if(prevX == targetX && prevY == targetY) continue; bool isBottom = targetY - prevY < 0; bool isLeft = targetX - prevX < 0; double a = (targetY - prevY) / (targetX - prevX), fracA=1/a; double b = targetY - a * targetX; double leftBorder = m_bottomLeftX + currentIndexX * stepX, bottomBorder = m_bottomLeftY + currentIndexY * stepY; CrossPosition[0] = (leftBorder + (isLeft ? 0 : stepX)) * a + b; CrossPosition[1] = (bottomBorder + (isBottom ? 0 : stepY) - b) * fracA; while ( (targetY < CrossPosition[0] == isBottom && Math.Abs(targetY - CrossPosition[0]) / stepY > 1E-9) || (targetX < CrossPosition[1] == isLeft && Math.Abs(targetX - CrossPosition[1]) / stepX > 1E-9) )
私のソースデータはポイントのセットです。 知られていないことについて-測定されたプロセスは連続的ですが、プロセス自体は完全にarbitrary意的です。異なる容量のランダムな干渉に対して、付加的な干渉が発生して消滅する可能性があります。 この場合、唯一の解決策は線形補間です。 入力データが小さいため、ラティスノードを通る直線の通過に関連するエラーは許容されません。
これらの条件を考えると、任意の次元に拡張できる普遍的なソリューションは、正方形から正方形への段階的な移行です。 (デモコードでは、ラインが垂直または水平である場合は考慮されない場合、すぐに警告します)
クラス全体 public class MinkowskiDimension { public MinkowskiDimension(int startSize, int finishSzie) { StartSize = startSize; FinishSize = finishSzie; } public MinkowskiDimension() { } public int StartSize { get { return m_startSize; } set { m_startSize = value; if (m_startSize < m_finishSize) { m_scaleArgument = new double[m_finishSize - m_startSize]; for (int i = 0; i != m_scaleArgument.Count(); ++i) m_scaleArgument[i] = - Math.Log(m_startSize + i); m_boxesNumber = new double[m_scaleArgument.Count()]; } } } int m_startSize; public int FinishSize { get { return m_finishSize; } set { m_finishSize = value; m_Boxes = new bool[value, value]; if (m_startSize < m_finishSize) { m_scaleArgument = new double[m_finishSize - m_startSize]; for (int i = 0; i != m_scaleArgument.Count(); ++i) m_scaleArgument[i] = Math.Log(m_startSize + i); m_boxesNumber = new double[m_scaleArgument.Count()]; } } } int m_finishSize; double[] m_scaleArgument; double[] m_boxesNumber; public double calculate(IEnumerable<KeyValuePair<double, double>> dataList) { double minY = Double.MaxValue, maxY = Double.MinValue; double minX = minY, maxX = maxY; foreach (var pair in dataList) { if (minY > pair.Value) minY = pair.Value; if (maxY < pair.Value) maxY = pair.Value; if (minX > pair.Key) minX = pair.Key; if (maxX < pair.Key) maxX = pair.Key; } m_bottomLeftY = minY; m_bottomLeftX = minX; return calculate(dataList, maxX, maxY); } public double calculate(IEnumerable<KeyValuePair<double, double>> dataList, double maxX, double maxY) { if( dataList.Count() < 2) return 0; for(int scaleNumber = StartSize; scaleNumber !=FinishSize; ++scaleNumber){ double XScale = (maxX - m_bottomLeftX) / scaleNumber; double YScale = (maxY - m_bottomLeftY) / scaleNumber; var enumerator = dataList.GetEnumerator(); fillBoxes( (ref double x, ref double y) => { var res = enumerator.MoveNext(); if (res) { x = enumerator.Current.Key; y = enumerator.Current.Value; } return res; }, XScale, YScale); int count = calculatedNumberBoxesAndIbit(scaleNumber); if (count == 0) count = 1; m_boxesNumber[scaleNumber - StartSize] = Math.Log(count); } m_linearApproximator.approximate(m_scaleArgument, m_boxesNumber); return m_linearApproximator.resultPolinomal.a[1]; } double m_bottomLeftX, m_bottomLeftY; void fillBoxes(GetDataDelegate dataIterator, double stepX, double stepY) { double prevX=0, prevY=0, targetX=0, targetY=0; dataIterator(ref prevX, ref prevY); int indexY = FinishSize, indexX = FinishSize; int currentIndexX= calculateIndex(m_bottomLeftX, stepX, prevX), currentIndexY =calculateIndex(m_bottomLeftY, stepY, prevY) ; m_Boxes[currentIndexY, currentIndexX] = true; double[] CrossPosition = new double[2]; while (dataIterator(ref targetX, ref targetY)) { if(prevX == targetX && prevY == targetY) continue; bool isBottom = targetY - prevY < 0; bool isLeft = targetX - prevX < 0; double a = (targetY - prevY) / (targetX - prevX), fracA=1/a; double b = targetY - a * targetX; double leftBorder = m_bottomLeftX + currentIndexX * stepX, bottomBorder = m_bottomLeftY + currentIndexY * stepY; CrossPosition[0] = (leftBorder + (isLeft ? 0 : stepX)) * a + b; CrossPosition[1] = (bottomBorder + (isBottom ? 0 : stepY) - b) * fracA; while ( (targetY < CrossPosition[0] == isBottom && Math.Abs(targetY - CrossPosition[0]) / stepY > 1E-9) || (targetX < CrossPosition[1] == isLeft && Math.Abs(targetX - CrossPosition[1]) / stepX > 1E-9) )
すべての可能な直線でテストしてみましょう:
[TestMethod] public void lineDimensionTest() { var m_calculator = new MinkowskiDimension(3, 10); var data = new List <KeyValuePair<double, double>>(); data.Add(new KeyValuePair<double, double>(0, 1)); data.Add(new KeyValuePair<double, double>(1, 5)); double result = m_calculator.calculate(data); if (Math.Abs(result - 1) > 1E-9) Assert.Fail(); data.Add(new KeyValuePair<double, double>(2, 9)); result = m_calculator.calculate(data); if (Math.Abs(result - 1) > 1E-9) Assert.Fail(); data.Clear(); data.Add(new KeyValuePair<double, double>(0, -1)); data.Add(new KeyValuePair<double, double>(1, -5)); data.Add(new KeyValuePair<double, double>(2, -9)); result = m_calculator.calculate(data); if (Math.Abs(result - 1) > 1E-9) Assert.Fail(); data.Clear(); data.Add(new KeyValuePair<double, double>(0, -1)); data.Add(new KeyValuePair<double, double>(0.5, -3)); data.Add(new KeyValuePair<double, double>(2, -9)); result = m_calculator.calculate(data); if (Math.Abs(result - 1) > 1E-9) Assert.Fail(); }
うまく機能します 正方形を見てみましょう。 ああ、私が警告したことに出くわしました。 しかし、問題ではないので、正方形を裏返して、縮退したケースを追加しましょう。
[TestMethod] public void squareDimensiontest() { var m_calculator = new MinkowskiDimension(3, 15); var data = new List<KeyValuePair<double, double>>(); data.Add(new KeyValuePair<double, double>(0, 1)); data.Add(new KeyValuePair<double, double>(1, 0)); data.Add(new KeyValuePair<double, double>(0, -1)); data.Add(new KeyValuePair<double, double>(-1, 0)); data.Add(new KeyValuePair<double, double>(0, 1)); double result = m_calculator.calculate(data); if (Math.Abs(result - 2) > 1E-9) Assert.Fail(); }
結果
1.1 Brr、なんて奇妙だ。 しかし、もちろん、2は平面図用であり、長方形用であり、その輪郭用ではありません。 まあ、それは理解できます。 スケールの数を追加しましょう。 1.05; さらに追加; 団結のために努力します。
有限集合の集合の場合、ミンコフスキー次元は各集合の次元の最大値であることがわかります。 つまり 線のセットの場合、次元
1 。 つまり、結果は完全に正しいです。
さて、あなたは教皇が正方形と変わらないことを証明することができます。 なぜなら 輪郭を直線で表す場合、領域は三角形または正方形に分割されます。 私たちは皆、広場について知っています。 正方形のミンコフスキー次元は何ですか?2.そして三角形の場合は?
}{\ln(\epsilon)}=\lim\limits_{\epsilon\to0}\frac{\ln&space;0.5&space;a-\ln\epsilon^2}{-\ln\epsilon}=2)
それは奇妙ではなく、2つです。 ちなみに、これは、フラクタル次元が曲線の非滑らかさを反映するという元の記事の仮定を破ります。 ところで、主なことは、結果として、デジタル化された司祭教皇の最大次元は2と2であるということです。
別の興味深い例。 円の大きさは?
}{\ln(\epsilon)}=\lim\limits_{\epsilon\to0}\frac{\ln&space;\pi&space;a-\ln\epsilon^2}{-\ln\epsilon}=2)
また2。 そして円?
}{\ln(\epsilon)}=\lim\limits_{\epsilon\to0}\frac{\ln&space;\pi&space;a-\ln\epsilon}{-\ln\epsilon}=1)
合計:円、正方形、三角形(およびロペス司祭)は私たちと見分けがつかないため、フラクタル次元のモデル解釈に重大な困難をもたらします。 直線のデータ間の古典的な補間により、輪郭の次元は1になり、面積は2になる傾向があります。 したがって、先験的な知識がなければ、その計算は意味を失います。 まあ、私たちの小さなテストでも、複雑な曲線の向きが計算に強い摂動をもたらし、パラメータ自体が何を示しているのかを理解せずにそれらの推定が非常に難しいことを示しました。