Geekly Articles each Day

浮動小数点演算のエラー補正

この作業は、浮動小数点数の計算で生じる丸め誤差に当てられています。 ここでは、「実数の表現」、「浮動小数点数の丸め誤差を見つける方法」、および丸め誤差の補正の例について簡単に説明します。

このペーパーでは、プログラミング言語Cで例を示します。

実数の表現


IEEE 754-2008標準の最終実数の表現を、 S （0または1）、仮数部M、および次数Eの 3つの要素で特徴付けられる式の形式で考えてみましょう。

v = -1 S * b （E-バイアス） * M


次の表は、標準の浮動小数点数形式のパラメーターを示しています。 ここで、 wは次数を表すビットフィールドの幅、 tは仮数を表すビットフィールドの幅、 kはビット文字列の合計幅です。



次の表は、標準の32ビットおよび64ビット浮動小数点の実際の形式のバリエーションと精度の範囲を示しています。



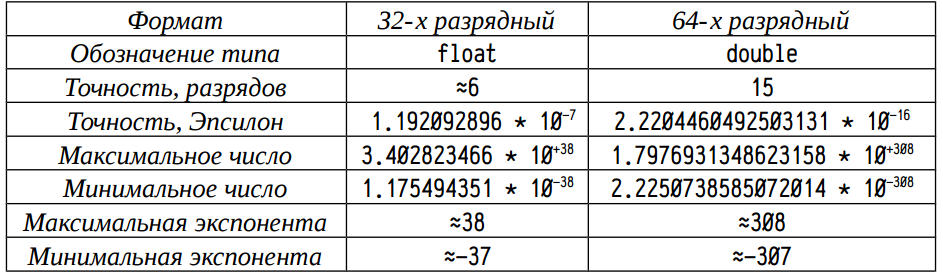
ここで、「精度、イプシロン」は、式が真である最小数です。

 1 + EPSILON != 1


このEpsilon値は、加算および減算演算の相対的な精度を特徴づけます。xに加算される値またはxから減算される値がepsilon * xより小さい場合、結果はxに等しくなります。 実際には、場合によっては、加法演算でイプシロン* xに近い数量を使用すると、より短い期間の丸め誤差が影響し始めます。 このような状況については、このペーパーで説明します。

データ型float（Binary32）の実数の表現を検討してください。



この例では：


したがって、数V = 1.01 2 * 2 10 -3 10 = 101 2 * 2 10 -5 10 = 5 10 * 2 10 -5 10 = 0.15625 10

実数で演算を実行する場合、結果はしばしばNビット行列に適合しないことに注意してください。 丸めが発生します。 1つの計算操作での丸めはEPSILON / 2の次数を超えませんが、多くの操作を行う必要がある場合、結果の計算の精度を向上させるために、特定の各操作の結果がどのように丸められるかを正確に見つける方法を学ぶ必要があります。

丸めと公理の違反の詳細については、ファイルmakarov_float.pdf （以下の資料へのリンク）を参照してください 。

浮動小数点数の丸め誤差を見つける方法


この問題は多くの専門家によって調査されました。その中で最も有名なのは、デビッドゴールドバーグ、ウィリアムカヘン、ジョナサンリチャードシェフチュクです。

以下に、Shevchukの研究で与えられた丸め誤差を見つけるアルゴリズムを、例として2つの関数を使用して検討します。


これらのアルゴリズムを正しく理解するために、Shevchukの研究で考慮されている定理に依存します。 定理は証明なしで与えます。

数aがpビット数であるとすると、それは数aのマチス長がpビットで表されることを意味します。

トゥーサム


定理：数値aとbをpビットの浮動小数点数とし、 p > = 3の場合、このアルゴリズムに従って、2つの数値xとyを取得します。条件はa + b = x + yです。 さらに、 xはaとbの合計の近似値であり、 yは数値xの計算の丸め誤差です。



Twoproduct


実際、2つの実数を乗算するときに丸め誤差を見つけるためのアルゴリズムは、2つの関数で構成されます。分割-補助関数と、誤差を見つけるTwoProduct関数です。

Split関数のアルゴリズムを検討してください。

スプリット

定理：数値aはpビットの浮動小数点数で、 p > = 3です。ここで、 p / 2 <= s <= p -1のブレークポイントsを選択します。 アルゴリズムに従って、（ p - s ）-ビット番号-番号a_hiおよび（ s -1）-ビット番号-a_loを取得します。 a_hi | > = | a_low | およびa = a_hi + a_low 。



次に、TwoProduct関数の分析に移りましょう。

Twoproduct

定理：数値aとbをpビットの浮動小数点数とします。ここで、 p > = 6です。次に、このアルゴリズムを実行すると、2つの数値xとyが得られ、条件が満たされます： a * b = x + y 。 さらに、 xは数値aとbの積の近似値であり、数値yは数値xの計算の丸め誤差です。



最終結果は、結果とエラーというNビットの実数のペアで表されることがわかります。 さらに、2番目の順序は、最初の順序に対してEPSILONを超えないようにする必要があります。

浮動小数点数の丸め誤差の補正の例


次に、Shevchukのアルゴリズムに基づいた実用的な計算に戻ります。 浮動小数点数の加算と乗算で丸め誤差を見つけ、誤差が累積する方法を分析します。

合計丸め誤差


簡単な加算プログラムの例を次に示します。

 #include <stdio.h> #include <math.h> int main() { float val = 2.7892; printf("%0.7g \n", val); val = val/10000000000.0; float result = 0.0; for (long long i = 0; i < 10000000000; i++) { result += val; } printf("%0.7g \n", result); return 0; }

プログラムの結果、2.7892と2.7892の2つの同一の数値が得られます。 ただし、コンソール出力は2.7892および0.0078125でした。 これは、エラーが非常に大きく蓄積したことを示しています。

今度は同じことをしようとしますが、Shevchukアルゴリズムを使用して、別の変数にエラーを蓄積し、合計のメイン変数にエラーを追加して結果を補正します。

 #include <stdio.h> #include <math.h> float TwoSum(float a, float b, float& error) { float x = a + b; float b_virt = x - a; float a_virt = x - b_virt; float b_roundoff = b - b_virt; float a_roudnoff = a - a_virt; float y = a_roudnoff + b_roundoff; error += y; return x; } int main() { float val = 2.7892; printf("%0.7g \n", val); val = val/10000000000.0; float result = 0.0; float error = 0.0; for (long long i = 0; i < 10000000000; i++) { result = TwoSum(result, val, error); } result += error; printf("%0.7g \n", result); return 0; }

その結果、2.7892と0.015625の2つの数値が得られます。 結果は改善されましたが、エラーはまだ感じられます。 この例では、TwoSum（）関数では加算操作で発生したエラーが考慮されていません。

 error += y;

サイクルの各反復で結果を補正し、加算操作で丸め誤差を累積する変数の誤差を上書きします。 これを行うには、TwoSum（）関数を変更します。エラーを蓄積する必要があるか、または書き換える必要があるかを示すbool型のisNull変数を追加します 。

結果として、結果は2つの変数で表されます。 結果はメイン変数、エラー1は演算結果のエラー+ = valです。

コードは次のようになります。

 #include <stdio.h> #include <math.h> float TwoSum(float a, float b, float& error, bool isNull) { float x = a + b; float b_virt = x - a; float a_virt = x - b_virt; float b_roundoff = b - b_virt; float a_roudnoff = a - a_virt; float y = a_roudnoff + b_roundoff; if (isNull) { error = y; } else { error += y; } return x; } int main() { float val = 2.7892; printf("%0.7g \n", val); val = val/10000000000.0; float result = 0.0; float error1 = 0.0; for (long long i = 0; i < 10000000000; i++) { result = TwoSum(result, val, error1, false); result = TwoSum(error1, result, error1, true); } printf("%0.7g \n", result); return 0; }

プログラムは、2,7892と2,789195の数字を出力します。

ここで、乗算演算で発生する丸め誤差は考慮されていないことに注意してください。

 val = val*(1/10000000000.0);


D.R.によって開発された乗算エラーのアカウンティング機能を追加することにより、このエラーを考慮します。 シェフチュク。 この場合、変数valは2つの変数で表されます。

 val_real = val + errorMult

したがって、 結果は3つの変数で表されます。 結果はメイン変数、 error1は演算結果+ = valのエラー、 error2は演算結果+ = errorMultのエラーです。

また、 error1およびerror2変数を追加し、この操作からのエラーをerror2に書き込みます。

その結果、コードは：

 #include <stdio.h> #include <math.h> float TwoSum(float a, float b, float& error, bool isNull) { //isNull   ,       //      float x = a + b; float b_virt = x - a; float a_virt = x - b_virt; float b_roundoff = b - b_virt; float a_roudnoff = a - a_virt; float y = a_roudnoff + b_roundoff; if (isNull) { error = y; } else { error += y; } return x; } void Split(float a, int s, float& a_hi, float& a_lo) { float c = (pow(2, s) + 1)*a; float a_big = c - a; a_hi = c - a_big; a_lo = a - a_hi; } float TwoProduct(float a, float b, float& err) { float x = a*b; float a_hi, a_low, b_hi, b_low; Split(a, 12, a_hi, a_low); Split(b, 12, b_hi, b_low); float err1, err2, err3; err1 = x - (a_hi*b_hi); err2 = err1 - (a_low*b_hi); err3 = err2 - (a_hi*b_low); err += ((a_low * b_low) - err3); return x; } int main() { float val = 2.7892; printf("%0.7g \n", val); float errorMult = 0;//  val = TwoProduct(val, 1.0/10000000000.0, errorMult); float result = 0.0; float error1 = 0.0; float error2 = 0.0; for (long long i = 0; i < 10000000000; i++) { result = TwoSum(result, val, error1, false); result = TwoSum(result, errorMult, error2, false); error1 = TwoSum(error2, error1, error2, true); result = TwoSum(error1, result, error1, true); } printf("%0.7g \n", result); return 0; }

次の番号がコンソールに表示されました：2.7892および2.789195。

これは、乗算の丸め誤差が、100億回の反復でも十分に小さいことを示唆しています。 この結果は、加算と乗算の演算におけるエラーを考慮して、元の数に可能な限り近いものです。 より正確な結果を得るために、エラーを考慮した追加の変数を入力できます。 たとえば、TwoSum（）関数で基本エラーを累積する操作のエラーを考慮した変数を追加します。 次に、このエラーは、主な結果に関してEPSILON 2のオーダーになります（最初のエラーはEPSILONのオーダーになります）。

乗算丸め誤差


サイクルの数1.0012 101を計算します。 次のことを行います。

 #include <stdio.h> #include <math.h> int main() { float val = 1.0012; float result = 1.0012; for (long long i = 0; i < 100; i++) { result *= val; } printf("%0.15g \n", result); return 0; }

小数点以下15桁までの正確な結果は1.128768638496750であることに注意してください。 受け取ります：1.12876391410828。 ご覧のとおり、エラーは非常に大きいことがわかりました。

変数valを派生させてdoubleデータ型に変換し、実際に変数に書き込まれたものを確認します。

 printf("%0.15g \n", (double)val);

番号1.00119996070862を取得します。 これは、プログラミングでは、最も正確な定数でさえ信頼性も定数でもないことを示唆しています。 したがって、実際の正確な結果は1.128764164435784で、小数点以下15桁まで正確です。

それでは、以前に取得した結果を改善してみましょう。 これを行うために、乗算演算の丸め誤差を考慮して、計算結果の補正を導入します。 また、各ステップで結果変数に累積エラーを追加しようとします。

コード：

 #include <stdio.h> #include <math.h> float TwoSum(float a, float b, float& error, bool isNull) { //isNull   ,       //      float x = a + b; float b_virt = x - a; float a_virt = x - b_virt; float b_roundoff = b - b_virt; float a_roudnoff = a - a_virt; float y = a_roudnoff + b_roundoff; if (isNull) { error = y; } else { error += y; } return x; } void Split(float a, int s, float& a_hi, float& a_lo) { float c = (pow(2, s) + 1)*a; float a_big = c - a; a_hi = c - a_big; a_lo = a - a_hi; } float TwoProduct(float a, float b, float& err) { float x = a*b; float a_hi, a_low, b_hi, b_low; Split(a, 12, a_hi, a_low); Split(b, 12, b_hi, b_low); float err1, err2, err3; err1 = x - (a_hi*b_hi); err2 = err1 - (a_low*b_hi); err3 = err2 - (a_hi*b_low); err += ((a_low * b_low) - err3); return x; } int main() { float val = 1.0012; float result = 1.0012; float errorMain = 0.0; for (long long i = 0; i < 100; i++) { result = TwoProduct(result, val, errorMain); result = TwoSum(errorMain, result, errorMain, true); } printf("%0.15g \n", result); return 0; }

プログラムは次の番号を表示します：1.12876415252686。 1.0e-008のエラーが発生しました。これは、 floatデータ型の EPSILON / 2未満です。 したがって、この結果は非常に良いと考えることができます。

まとめ


1）このペーパーでは、IEEE 754-2008標準の形式での浮動小数点数の表現を検討しました。
2）浮動小数点数の加算および乗算で丸め誤差を見つける方法が示されました。
3）浮動小数点数の丸め誤差を補正する簡単な例を検討しました。

作業はビクターファデエフによって行われました。
Makarov A.V.にアドバイス

PSユーザーに見つかったエラーに感謝します。
xeioex 、 アルボム 。

中古文学


Source: https://habr.com/ru/post/J266023/

More articles:


All Articles