多くの問題では、疑似乱数ジェネレーターを使用する必要があります。 ですから、私たちにはそのようなニーズがあります。 一般に、タスクは
RB8V7ブロックに基づくコンピューティングプラットフォームを作成することでした。これは、特定の科学的問題を計算するためのアクセラレーターとして使用されるべきでした。
この科学的課題について少し説明します。1分程度の時間で生体微小管のダイナミクスを計算する必要がありました。 計算は、科学グループで開発された微小管の分子力学的モデルを使用した計算でした。 得られた計算結果に基づいて、微小管の動的不安定性のメカニズムについて結論を引き出すことが可能になることが計画されました。 アクセラレータを使用する必要があるのは、1分が十分に多くの計算ステップ(〜10 ^ 12)に相当し、その結果、計算に費やされる時間が長いためです。したがって、この記事のトピックに戻ると、このケースでは、言及した微小管の分子の熱運動を考慮するために、擬似乱数ジェネレーターが必要でした。
DMA転送をサポートするアーキテクチャは、プロジェクトの基本アーキテクチャとして使用されました。 このコンピューティングプラットフォームのコンポーネントとして、クロックサイクルごとに新しいタイプの擬似ランダム正規分布型フロートを生成でき、FPGAで可能な限り少ないリソースを消費するIPコアを実装する必要がありました。
詳細最後の要件は、第一に、このIPコアに加えて、他のコンピューティングモジュール+インターフェイスパーツがFPGAに存在する必要があり、第二に、問題の計算がfloatのような浮動小数点数で実行されたという事実によるものでしたFPGAは非常に多くのリソースを消費し、第三に、いくつかのコアがFPGA上にあるはずでした。 サイクルごとに乱数を生成する要件は、実際にはこれらの乱数を使用した最終的なコンピューティングモジュールのアーキテクチャによるものでした。 アーキテクチャはコンベアであったため、サイクルごとに新しい乱数が必要でした。
最後に、すべてがうまくいきましたが、この問題を解決するための道は間違った手順とエラーがないわけではないことに注意してください。 この記事がお役に立てば幸いです。
この問題を解決するために、RTLコードで高レベルのトランスレーターを使用しました。 複雑な計算タスクを実装するために、このアプローチにより、むき出しのRTLを使用するよりもはるかに高速に(多くの場合より優れた)結果を得ることができます。 特別なディレクティブを使用してC / C ++コードをRTLコードに変換する
Vivado HLSプログラムバージョン2014.4を使用しました。 ディレクティブの例は
ここにあります 。
開発中のソリューションに関する前述の要件と、ジェネレーターに複数の計算段階を含める必要があるという事実を考慮すると、パイプラインは最適なアーキテクチャです。 FPGAパイプラインの実装の詳細については、
こちらをご覧ください 。 コンピューティングパイプラインの主な特徴は、初期化間隔と待機時間であることに注意してください。 初期化間隔は、コンベアステップの実行に費やされたティック数です(すべてのステップの中で最大)。
レイテンシは、データがパイプライン入力に入った瞬間からパイプラインによる結果の出力までに経過したクロックサイクルの数です。 この場合、レイテンシはパイプラインの推定合計動作時間と比較して無視できるため、あまり興味深いものではありませんが、パイプラインがデータを受信できる頻度を実際に特徴付けるため、初期化間隔は非常に慎重にとる必要があります。彼がどれくらいの頻度で新しい結果を生み出すことができるか。
最初は、次のアプローチを使用することが決定されました。
- 均一に分布した乱数の独立した整数を取得するための線形フィードバックシフトレジスタ 。 最初は、それぞれの「シード」番号を使用して開始されます。 シード。
- 中心極限定理。これにより、多数の独立したランダム変数の合計が正規分布に近い分布を持つと述べることができます。 この例では、12個の数値が合計されます。
コード#pragma HLS PIPELINE unsigned lsb = lfsr & 1; lfsr >>= 1; if (lsb == 1) lfsr ^= 0x80400002; return lfsr;
このアプローチの利点のうち、この通常数のジェネレーターは最終スキームで非常に簡単に実装され、実際にはそれほど多くはかかりません。 このアプローチの主な欠点は、この方法では間違っていることです。 =)実際、ジェネレーターが提供する連続値は相関しています。 これは、自己相関関数(図を参照)を構築することによって、またはx [i]にx [i + k]をプロットすることによって明確に実証できます。ここで、k = 1,2,3 ...
このエラーにより、微小管のダイナミクスに興味深い効果が生じ、その運動はこのジェネレーターを使用してモデル化されました。

そのため、均一に分布した整数を生成するアルゴリズムを変更する必要がありました。 その選択
はメルセンヌの
旋風にかかった 。 このアルゴリズムでは、生成された数値の値が相互に相関していないという事実は、結果の数値シーケンスの自己相関関数を調べることで確認できます。 ただし、このアルゴリズムの実装には、サイズ612の数値フィールドで動作し、前の場合のように単一の数値では動作しないため、より多くのリソースが必要です(
パブリックドメインのコードを参照)。
「手続きにはnサイクル(ステップ)かかります」という言葉で理解できる予約をすぐに行います。 これは、RTLへの変換中にこの手順がnクロックパルスで実行されることを意味します。 たとえば、パイプラインの次のステップでシングルポートRAMメモリから2ワードを読み取る必要がある場合、ポートが1つしかないため、この操作は2サイクルで実行されます。つまり、メモリはサイクルごとに1つの書き込みまたは読み取り要求のみを提供できます。このアルゴリズムをRTLに最適に変換するには、コードを処理する必要がありました。 まず、ジェネレーター内の初期実装では、次が発生します。新しい乱数が要求されると、出力は次のマトリックス要素であるか、マトリックスの最後に到達するとマトリックス要素が更新されます。 更新手順は、配列要素を使用するさまざまなビットごとの操作で構成されます。 各要素の値が更新されるため、手順は少なくとも612ステップかかります。 その場合、出力は行列のゼロ要素です。 したがって、プロシージャは、この関数の呼び出しごとに異なる数のステップを実行します。 このような関数はパイプライン化できません。
オプション0 unsigned long y; if (mti >= N) { int kk; if (mti == N+1) sgenrand(4357); for (kk=0;kk<NM;kk++) { y = (mt[kk]&UPPER_MASK)|(mt[kk+1]&LOWER_MASK); mt[kk] = mt[kk+M] ^ (y >> 1) ^ mag01[y & 0x1]; } for (;kk<N-1;kk++) { y = (mt[kk]&UPPER_MASK)|(mt[kk+1]&LOWER_MASK); mt[kk] = mt[kk+(MN)] ^ (y >> 1) ^ mag01[y & 0x1]; } y = (mt[N-1]&UPPER_MASK)|(mt[0]&LOWER_MASK); mt[N-1] = mt[M-1] ^ (y >> 1) ^ mag01[y & 0x1]; mti = 0; } y = mt[mti++]; y ^= (y >> 11); y ^= (y << 7) & 0x9d2c5680UL; y ^= (y << 15) & 0xefc60000UL; y ^= (y >> 18); return ( (double)y * 2.3283064370807974e-10 );
この手順を変更します。関数の1回の呼び出しで、以前の配列要素が更新され、現在の要素が返されます。 現在、この手順は常に同じ数の手段を取ります。 さらに、結果は両方の実装で同じです。マトリックストラバーサルの最後に、すでに更新された値で満たされているため、単純に配列のゼロ要素に戻ることができます。 現在、この手順は実際にパイプライン化されています。
オプション1 #pragma HLS PIPELINE #pragma HLS INLINE float y; unsigned long mt_temp,reg1; unsigned long temper, temper1; if (mti<N_period-M_period) { mt_temp = (mt[mti]&UPPER_MASK)|(mt[mti+1]&LOWER_MASK); mt[mti] = mt[mti+M_period] ^ (mt_temp >> 1) ^ mag01[mt_temp & 0x1UL]; }else{ if (mti<N_period-1) { mt_temp = (mt[mti]&UPPER_MASK)|(mt[mti+1]&LOWER_MASK); mt[mti] = mt[mti+(M_period-N_period)] ^ (mt_temp >> 1) ^ mag01[mt_temp & 0x1UL]; }else{ mt_temp = (mt[N_period-1]&UPPER_MASK)|(mt[0]&LOWER_MASK); mt[N_period-1] = mt[M_period-1] ^ (mt_temp >> 1) ^ mag01[mt_temp & 0x1UL]; } } reg1 = mt[mti]; if (mti == (N_period - 1)) mti = 0; else mti=mti+1; temper=tempering(reg1); temper1 = (temper==0) ? 1 : temper; y=(float) temper1/4294967296.0; return y;
ここで、このようなパイプラインが新しい乱数を生成できる頻度を自問します。 これを行うには、さらに明確にする必要があります。 使用された配列(mt)を実装するリソースは何ですか? レジスタまたはメモリを使用して実装できます。 レジスタベースの実装は、単一の初期化間隔を達成するための究極のコード最適化に関して最も単純です。 メモリセルとは異なり、各レジスタは個別にアクセスできます。
ただし、多数のレジスタを使用する場合、レジスタ間のパスに遅延が発生する可能性が高く、生成されるIPコアの動作周波数を下げる必要が生じます。 メモリ使用の場合、メモリブロックへの同時リクエストの数には制限があり、その理由はブロックポートの数が制限されているためです。 ただし、原則として、時間遅延の問題はありません。 リソースの制限により、この場合、メモリを使用して配列を実装することをお勧めします。 メモリアクセスの競合があるかどうか、およびそれらを解決できるかどうかを検討します。
では、FPGAの観点から、配列要素の要求がサイクルで同時にいくつ発生しますか? まず、各メジャーで配列の4つのセルを操作することに注意してください。 つまり、最初の近似では、3つの読み取りと1つのレコードという4つの同時要求をメモリに提供する必要があります。 さらに、1つの読み取りと1つのレコードが同じセルで発生します。
オプション2 #pragma HLS PIPELINE #pragma HLS INLINE float y; unsigned long mt_temp,reg1,reg2,reg3,result; unsigned long temper, temper1; if (mti<N_period-M_period) { reg2=mt[mti+1]; // read 0 reg3=mt[mti+M_period]; // read 1 }else{ if (mti<N_period-1) { reg2=mt[mti+1]; //read 0 reg3=mt[mti+(M_period-N_period)]; //read 1 }else{ reg2=mt[0]; //read 0 reg3=mt[M_period-1]; //read 1 } } reg1 = mt[mti]; //read 2 mt_temp = (reg1&UPPER_MASK)|(reg2&LOWER_MASK); result = reg3 ^ (mt_temp >> 1) ^ mag01[mt_temp & 0x1UL]; mt[mti]=result; //write if (mti == (N_period - 1)) mti = 0; else mti=mti+1; temper=tempering(result); temper1 = (temper==0) ? 1 : temper; y=(float) temper1/4294967296.0; return y;
解決する必要がある最初の問題は、同じセル内の読み取りと書き込みの競合を削除することです。 これは、関数の連続呼び出しの結果、同じセルからの読み取りが行われるため、前の呼び出しでは値を読み取ってレジスタに保存し、次の場合はレジスタから必要な番号を取得するだけで十分であることに注意してください ここで、2つの読み取りと1つのレコード(異なるメモリセル内)の3つの同時リクエストをメモリに提供する必要があります。
オプション3 #pragma HLS PIPELINE #pragma HLS INLINE float y; unsigned long mt_temp,reg1,reg2,reg3,result; unsigned long temper, temper1; if (mti<N_period-M_period) { reg2=mt[mti+1]; //read 0 reg3=mt[mti+M_period]; //read1 }else{ if (mti<N_period-1) { reg2=mt[mti+1]; //read 0 reg3=mt[mti+(M_period-N_period)]; //read 1 }else{ reg2=mt[0]; //read 0 reg3=mt[M_period-1]; //read 1 } } reg1 = prev_val; mt_temp = (reg1&UPPER_MASK)|(reg2&LOWER_MASK); result = reg3 ^ (mt_temp >> 1) ^ mag01[mt_temp & 0x1UL]; mt[mti]=result; //write prev_val=reg2; if (mti == (N_period - 1)) mti = 0; else mti=mti+1; temper=tempering(result); temper1 = (temper==0) ? 1 : temper; y=(float) temper1/4294967296.0; return y;
Vivado HLSでメモリクエリの競合を解決するためのいくつかのトリックがあります。まず、デュアルポートRAMメモリを介してアレイを実装するようにトランスレーターに指示するディレクティブを追加します。同じセルに。
#pragma HLS RESOURCE variable=mt1 core=RAM_2P_BRAM
次に、1つのメモリブロックではなく、複数のメモリブロックを介して配列を実装するようにトランスレータに指示するディレクティブがあります。 これにより、ポートの総数が増加し、同時リクエストの最大可能数が増加します。 たとえば、インデックス0 ... N / 2の配列要素を1つのメモリブロックに配置し、インデックスN / 2 + 1 ... N-1の要素を2番目のメモリブロックに配置することができます。 または、たとえば、インデックス2 * kの要素が1つのブロックに配置され、インデックス2 * k + 1の要素が別のブロックに配置されます。 ブロック数は2以上にできることに注意してください。 また、場合によっては、アレイへの同時リクエストの数を増やすことができます。
#pragma HLS array_partition variable=AB block factor=4
残念ながら、この場合の後者のアプローチは、配列をサイズが異なるいくつかのブロックに分割する必要があり、ディレクティブが方法を知らないため、純粋な形では適用できませんでした。 すべてのインデックスを通過する際に配列のどの要素がアクセスされるかを注意深く見ると、配列が3つの部分に分割され、各部分への同時クエリが2つ以下になることがわかります。

実際、この段階では、Vivado HLSトランスレーターが私たちが何を望んでいるかを頑固に理解したくなく、最終初期化間隔が1を超えていたため、最も長い時間がかかりました。コード。 稼いだ!
最終オプション #pragma HLS PIPELINE #pragma HLS RESOURCE variable=mt1 core=RAM_2P_BRAM #pragma HLS RESOURCE variable=mt2 core=RAM_2P_BRAM #pragma HLS RESOURCE variable=mt3 core=RAM_2P_BRAM #pragma HLS INLINE float y; unsigned long mt_temp,reg1,reg2,reg3,result, m1_temp,m2_temp, m3_temp; unsigned long temper, temper1; unsigned int a1,a2, a3,s2,s3; int mti_next=0; if (mti == (N_period - 1)) mti_next = 0; else mti_next=mti+1; if (mti_next==0) { s2=1; s3=2; a1=mti_next; a2=2*M_period-N_period-1; a3=0; } else if (mti_next < (N_period - M_period)) { s2 = 1; s3 = 3; a1 = mti_next; a2 = 0; a3 = mti_next-1; }else if (mti_next== (N_period - M_period)){ s2 = 2; s3 = 3; a2 = 0; a1 = 0; a3 = N_period-M_period-1; } else if (mti_next < M_period) { s2 = 2; s3 = 1; a1 = mti_next - (N_period - M_period)-1; a2 = mti_next - (N_period - M_period); a3 = 0; } else if (mti_next < (2*(N_period-M_period)+1)) { s2 = 3; s3 = 1; a1 = mti_next - (N_period - M_period)-1; a2 = 0; a3 = mti_next - M_period; } else { s2 = 3; s3 = 2; a1 = 0; a2 = mti_next - (2*(N_period-M_period)+1); a3 = mti_next - M_period; } // read data from bram m1_temp = mt1[a1]; m2_temp = mt2[a2]; m3_temp = mt3[a3]; if (s2 == 1) reg2 = m1_temp; else if (s2 == 2) reg2 = m2_temp; else reg2 = m3_temp; if (s3 == 1) reg3 = m1_temp; else if (s3 == 2) reg3 = m2_temp; else reg3 = m3_temp; reg1 = prev_val; mt_temp = (reg1&UPPER_MASK)|(reg2&LOWER_MASK); result = reg3 ^ (mt_temp >> 1) ^ mag01[mt_temp & 0x1UL]; // write process if (mti < (N_period - M_period)) mt1[mti] = result; else if (mti < M_period) mt2[mti-(N_period-M_period)] = result; else mt3[mti-M_period] = result; //save into reg prev_val=reg2; mti=mti_next; temper=tempering(result); temper1 = (temper==0) ? 1 : temper; y=(float) temper1/4294967296.0; return y;
したがって、3ポートのデュアルポートRAMメモリを使用して配列を実装しました。これにより、関数をパイプライン化し、単一の初期化間隔を提供できました。 つまり、均一に分布した擬似乱数のジェネレーターが機能するようになりました。 ここで、これらの数値から正規分布の擬似乱数を取得する必要があります。 中心極限定理を使用して以前のアプローチを取ることができます。 ただし、均一に分布した乱数のジェネレーターはより多くのリソースを必要とすることを思い出し、中央極限定理では12個のジェネレーターを実装する必要があります。
Box-Muller変換が選択されまし
た 。これにより、間隔(0,1)の2つの一様分布のランダム変数から2つの正規分布乱数を取得できます。さらに、12は実際にはそれほど大きな数ではないCLTのアプローチとは対照的に、変換の場合、分布が分析的にガウス分布となる数値を取得します。ここでもう少し詳細を見つけることができ
ます 。この変換は2つの方法で存在することに注意してください: この結果は、ジェネレーターが呼び出されるたびに生成されるわけではなく、2番目の方法ではより多くの計算が使用されますが、呼び出しごとに結果が保証されます。
すべてのステップで結果が必要なので、2番目のアプローチが使用されました。 さらに、各計算操作にディレクティブが適用され、DSPブロックを使用してこの操作を実装しないようにトランスレーターに指示します。 デフォルトでは、Vivado HLSは最大数のDSPブロックを使用して計算操作を実装します。 事実、パイプライン処理を考慮すると、必要なDSPブロックの数は、利用可能なDSPブロックの総数に比べて非常に多くなるということです。 水晶上の位置を考えると、大きな時間遅延が得られます。
#pragma HLS RESOURCE variable=d0 core=FMul_nodsp
その結果、次のアプローチを使用してカーネルを得ました。
- メルセンヌ渦アルゴリズムを使用した一様分布乱数の2つのジェネレータ
- 区間(0,1)に一様に分布する2つのランダム変数から、2つの正規分布乱数を受け取るBox-Muller変換
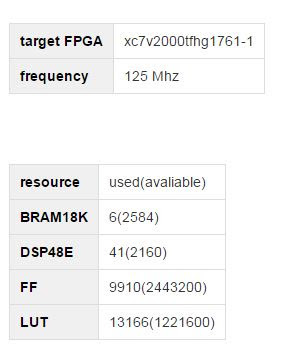
また、このジェネレーターを使用した微小管ダイナミクスの視覚化も引用します。
 PS: 実際、その後、メルセンヌの渦アプローチ+ Box-Muller変換を使用することは、正規分布の乱数を取得するための実際のアプローチであることが判明しました[1]。
PS: 実際、その後、メルセンヌの渦アプローチ+ Box-Muller変換を使用することは、正規分布の乱数を取得するための実際のアプローチであることが判明しました[1]。プロジェクトは
githubで入手できます。
質問やコメントを歓迎します。
[1] FPGAエディターを使用した高性能コンピューティング:Vanderbauwhede、Wim、Benkrid、Khaled(編)2013 pp。 20-30