このノートでは、1次元データの2種類のグラフ、つまり

• 棒グラフ
• 口ひげボックス

実数の任意のサンプルを考えます 、順序統計を示します そのような 。

棒グラフ

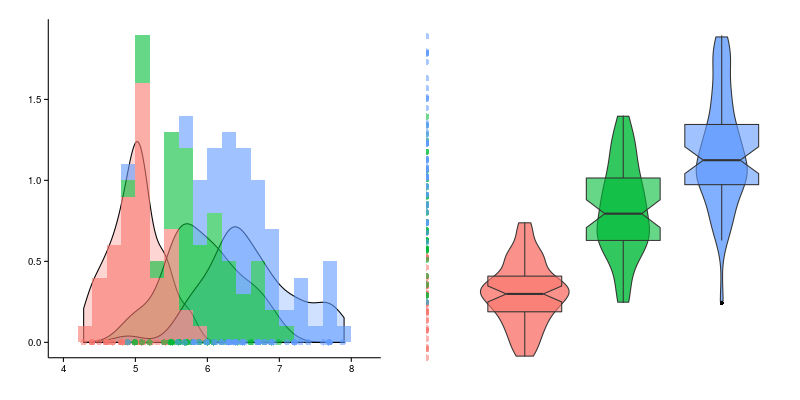
ほとんどの場合、誰もがこのタイプのスケジュールを学校や大学のプログラムから変更します。これは写真のようなものです。



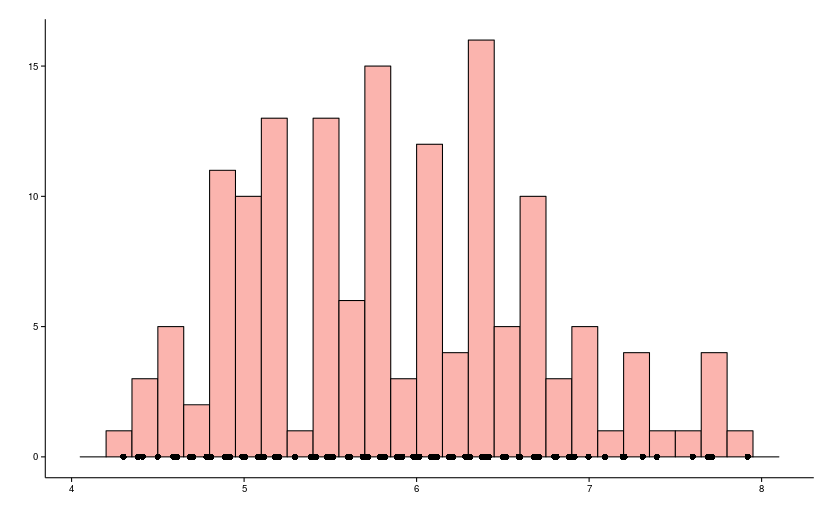
まず、入力サンプルの値がx軸にあり、y軸にこの値が発生した回数があることを覚えておく必要があります（サンプルと呼びましょう）。 ヒストグラムを使用すると、特異性を損なうことなく、データセットを粗くしてコンパクトにすることができます。
重要なヒストグラム機能は次のとおりです。

• 列数（ビンまたはバーと呼ばれる）
• y軸に沿った絶対値または密度の測定値
• データのグループ化方法

列

ほとんどの場合、ヒストグラムはセグメントで決定されます どこで -ソースサンプル 最も近い「読み取り可能な」数値に丸める補助定数。これは、それぞれの場合にスケールに依存し、通常、これらはソースデータのスケールの約数の約数です。 データを切り取る方法が突然面白くなった場合は、リンクR（pretty）を見ることができます。

また、ヒストグラムは通常、セグメントIを等しい長さのサブセグメントに分割します。ここでは、いくつかの式を指定できますが、セグメント数の選択は芸術です。

• スタージスルール（写真家ではありません）。
• スコットルール。
• フリードマン・ディーコネスのルール。

どこで 列数です -元のサンプルのサイズ、 -標準偏差の評価、 -四分位間の距離。これは以下にあります。

常識のいくつかのルールに注意することもできます

• ほとんどの列に複数のソース値があると便利です
• ヒストグラムの各列には少なくとも1ピクセルの幅が必要です。一般に、「200以下」列の制限は非常に一般的です

それ以外の場合、列の数が多すぎて、初期データが小さい場合、ヒストグラムはバーコードのようになります（下図を参照）。

Y軸

ヒストグラムは、各間隔に含まれる初期サンプルの要素数がy軸に沿ってプロットされている場合は絶対値であり、列の合計が1に正規化されている場合は相対的です。この場合、ヒストグラムは分布密度の推定値であり、スケールのみがグラフの観点から変化します。

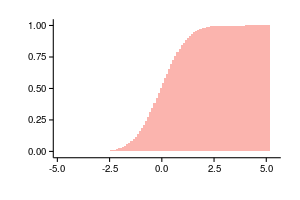
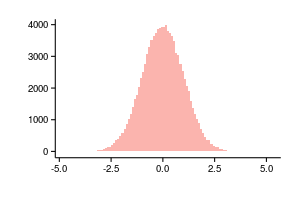
通常のヒストグラムは密度の推定値であるため、列を要約し、次のように確率関数の推定値を取得できます。 。 次の2つのグラフは、同じデータ、左側の正規化されたヒストグラム、および右側の正規化されたヒストグラムの累積値に基づいています。

データのグループ化

これまでのところ、見たいだけの特性がある場合を考慮してきましたが、通常、異なるサブグループの同じ特性の動作を比較する方がはるかに興味深いです。 この場合、ヒストグラムは次の形式になります。



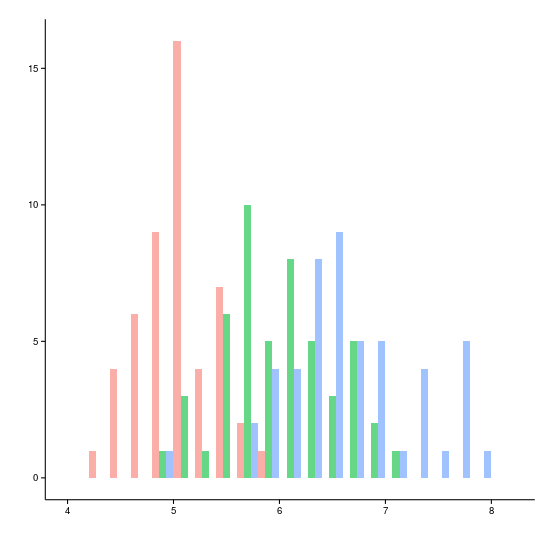
この場合、各グループの各列の幅はグループの数に比例して減少し、互いに対してわずかに移動します。代わりに、同じデータに対してこのように見える半透明のオーバーラップを考慮することができます。

乾燥残留物中

ヒストグラムを描画するには、定義する必要があります

• 列数
• データの正規化と蓄積は必要ですか？
• さまざまなグループを表示する方法

各グループのヒストグラムを描画するには、次の値を保存する必要があります。

• 列の境界値。最初の値 左端の列の左境界線の座標であり、最後の -右端の列の右境界線の座標
• 値-各列に入る要素の数。

スパンチャート

「口ひげのある箱」には正式に確立された名前はありません。「口ひげのある箱」と呼ぶと、特に複数の箱とスパン図がある場合、私の舌は回転しません。 左側にある3つのボックスの例を示します。ソースデータの対応する値が表示されます（それらはスパン図の一部ではありません）。 まず、スパンダイアグラムの場合、初期特性はY軸に沿ってプロットされ、X軸は条件付きでグループ化変数を表すことに注意してください。



ソースデータに関する1つのグループのボックスを描画するには、次の3つの特性のみを知る必要があります。

• 最初の四分位
• 中央値へ
• 第三四分位

次の追加のものが「必須」セットに追加される場合があります。

• 最低
• 最大
• 5パーセンタイル
• 95パーセンタイル
• 多くの極値 、

したがって、セクションに口ひげのあるボックスは次のようになります。



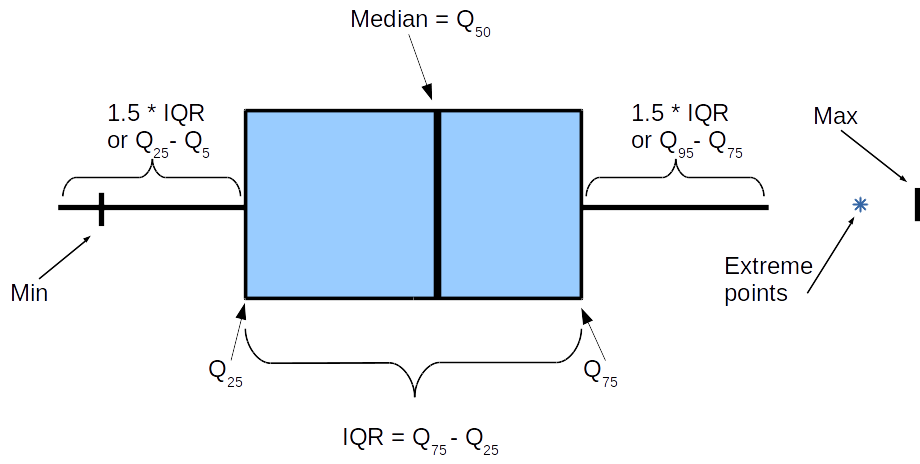
いくつかの点を明確にする必要があります。 ボックス、つまり、間のオブジェクト そして ほぼすべての場所でこれらの値によって制限されていますが、「口ひげ」はさまざまである可​​能性があり、数値に本当に興味がある場合は、個々のケースで何を意味するかを明確にする必要があります。 最も重要なことは、口ひげの長さです。 。

多くの場合、最小および最大マークはドロップされ、極端なポイント、つまり口ひげを超えるものもドロップされるか、ドットまたはアスタリスクで描画されます。 データ構造によっては、極端な値をレンダリングしたい場合、スパンチャートを描画するためのデータ量が大幅に増加する可能性があります。

マジックナンバー Tukey's Exploratory Data Analysis （1977）の作品に登場し、その出現の理由はあまり明確ではありませんが、それ以来何も変わっていません。多くのツールがデフォルト値として提供しますが、この場合、任意のゼロ口ひげ」は、ソースデータの最小値から最大値までのセグメント全体をカバーします。

という仮定があります 次のように発生しました。 口ひげの幅は 、それが知られている 対称分布の場合は、中央値からの絶対偏差 （MAD）と一致します。これは、係数による分散の推定値です。 。 それはつまり 、左に3シグマ、右に3シグマが不明になります。
時々、口ひげの終わりとして間隔が提案されます この場合、常に（初期データが20を超える場合）間隔内に収まらないポイントを取得する必要があるため、このアプローチでは通常無視されます。

乾燥残留物中

「スパンチャート」を描画するには、以下を決定する必要があります。

• データのグループ化方法
• 口ひげの長さ
• 極端な値に注意する必要がありますか

1つのグループに「口ひげボックス」を描くには、3つの数字だけが必要です。