先日、このリソースの聴衆にふさわしいと思われる興味深いタスクに出会いました。 条件は次のとおりです。

「12個で構成されるネットボックスが90％のケースで310±7グラムを超えないように、製造中のキャンディの質量の最大許容偏差を見つけます。 分配の法則は正常と見なされます。」

条件はインターネットから引き出されたり、楽しい仕事のリソースを覗かれたりしたのではなく、有名な製菓工場で生産を組織し、管理するためのエンジニアである非常に良い友人から来たと言う価値があります。 つまり、問題の起源は非常に現実的であり、その解決策は実用的です。

自分で問題を解決するように読者を招待しましたが、私よりもうまく対処できたと言わざるを得ません。 私の決断では、間違った仮定をしました。

1.コンベンション

ボックスのパラメーターを大きな文字で、キャンディーの小さな文字で示すことに同意しましょう。
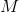
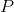
聞かせて そして -したがって、箱の正味質量とその許容値、 超えないケースの割合 。
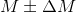
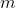
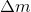
聞かせて そして -それぞれ、キャンディの質量とその耐性 超えないケースの割合 。
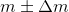
箱の中のキャンディーの数 。

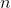
2.正規分布

正規分布は、ガウス関数によって記述されます。


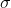
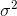
どこで -数学的な期待 -標準偏差、その平方 -分散と呼ばれます。

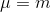
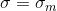
お菓子の場合 、 、したがって：


チョコレートの箱の場合 、 ：


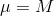
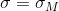
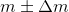
確率 キャンディの質量は超えないこと 等しい：


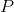
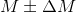
確率 ネットボックスが超えていないという事実 等しい：


以下の図は、上記のすべてをよく示しています。


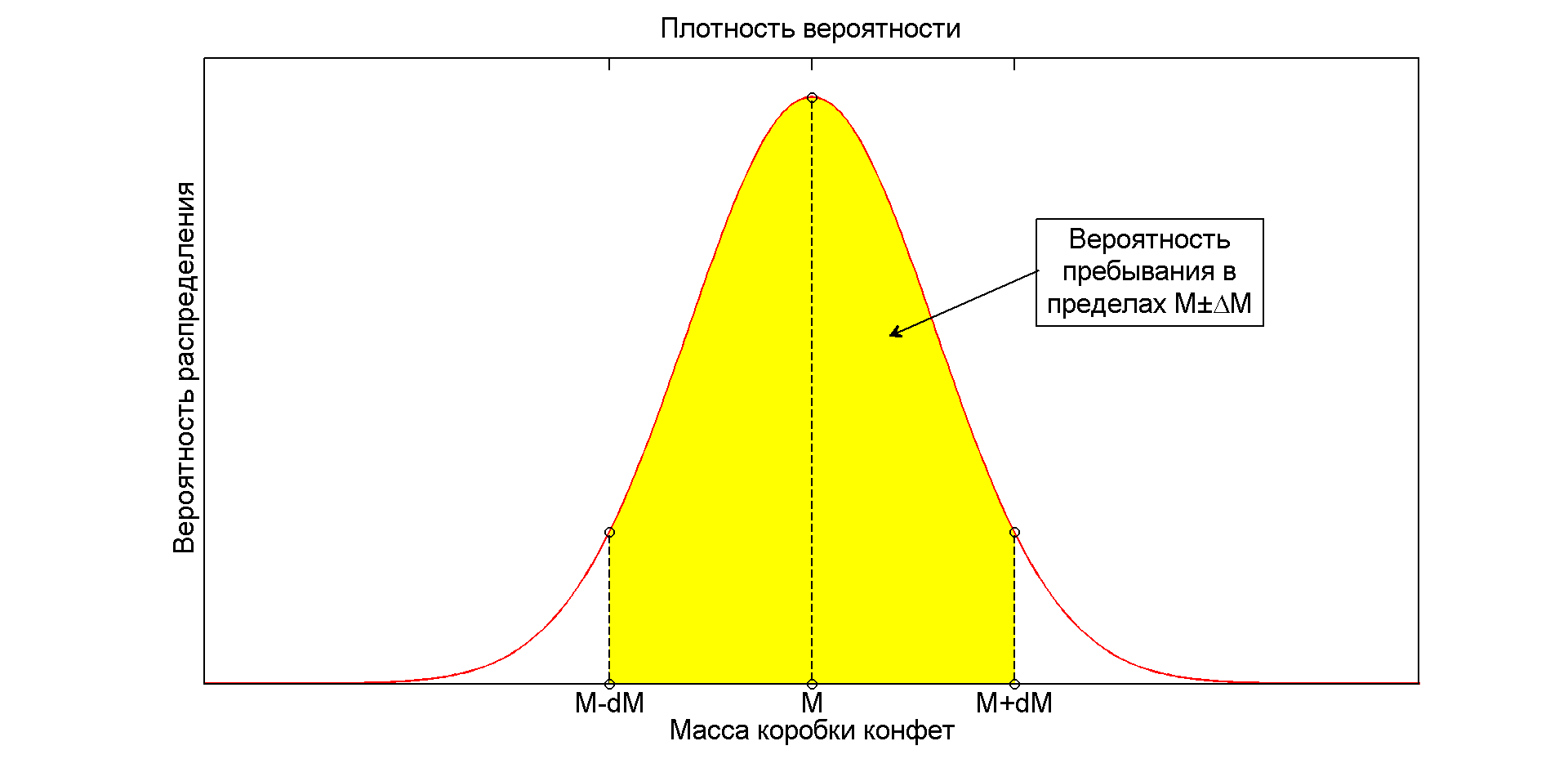
キャンディーの確率を見つける：


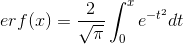
どこで 分布関数であり、 -エラー機能。

キャンディーの場合：


ボックスについても同様です：

3.中央極限定理

中心極限定理から、独立したランダム変数がある場合：


、その後の合計：

パラメータがあります：


私たちの状況に関連して、次のものがあります。

4.確率と私の間違い

私は誤って、箱の総確率は個々のキャンディーの確率の積に等しいと考えました。 言い換えれば：


どこから：

結果の連立方程式：


彼女に関する決定 ：

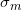
、推定：

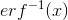
どこで -逆誤差関数で、非常に具体的な数値が見つかりました：








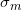
私はこの決定を次のように実証しました：キャンディの質量は、ケースの99.13％（115に1）で25.8333±3.2212を超えないことが必要です。 そして、この答えは矛盾していませんが、真実は 正解です。 このように標準偏差が小さいので、何も落とす必要はありません。多くの読者が長い間私に示唆していて、正しいことでした。

5.検証

彼女なしで。 matlabaでチェックを作成しました。 つまり、通常の法則に従って、見つかったパラメーターで1,000,000個のキャンディーを作成します。 ランダムな（同等の）方法で、それらからそれぞれ12個の1,000,000個のグループ（箱を数える）を形成します。 310±7を超えないグループの数をチェックし、合計で除算することにより、ボックスの確率を取得します。 そして1000回。


結果はとても美しいスケジュールです：


100万個のボックスは少数であり、その数を無限に向けると、確率は正確に90％になると思います。

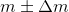
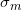
もっと興味深いケースは、キャンディー充填機が1.2285を超える一定の標準偏差を持ち、境界を見つける必要がある場合です。 その上で、与えられた 、キャンディは同じ条件を満たすために廃棄する必要があります。 これははるかに困難な作業であり、別の記事に専念できます。